In if mass of the sphere be denoted as 'm' and the acceleration of car be 'a' then $T_{2}$ is given by:

A

mg

B

$m {(g^{2} + a^{2})}^{1 / 2}$

C

$m {(g^{2} - a^{2})}^{1 / 2}$

D

$m (g + a)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$T_{1} = m g$

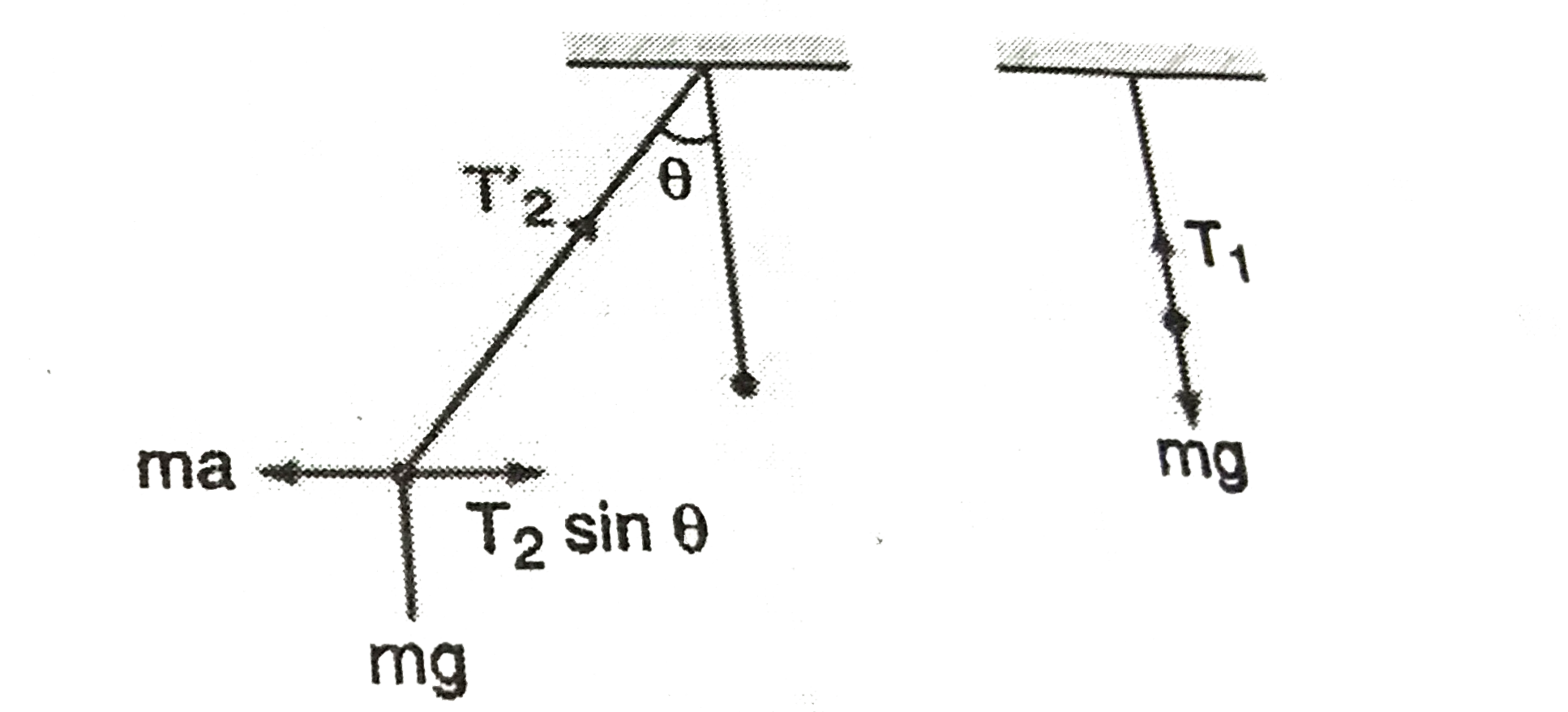
$T_{2} cos θ = M g$
$T_{2} = (\frac{M g}{cos θ})$
$T_{2} sin θ = m a$
$T_{2}^{2} = m^{2} a^{2} + m^{2} g^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15videos
FORCE AND NEWTONS LAWS OF MOTION
BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4videos
FORCE AND NEWTONS LAWS OF MOTION
BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30videos
FORCE AND NEWTONS LAWS OF MOTION
BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35videos
BASIC MATHEMATICS
BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11videos
FRICTION AND CIRCULAR MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
If x denotes displacement in time t and x=a cost, then acceleration is :-
Aa cos t
B $- a cos t$
Ca sin t
D $- a sin t$
Question 2 - Select One
The escape velocity of a sphere of mass $m$ is given by
A $\sqrt{\frac{2 G M m}{R_{e}}}$
B $\sqrt{\frac{2 G M}{R_{e}^{2}}}$
C $\sqrt{\frac{2 G M m}{R_{e}^{2}}}$
D $\sqrt{\frac{2 G M}{R_{e}}}$
Question 3 - Select One
The work done in time t on a body of mass m which is accelerated from rest to a speed v in time $t_{1}$ as a function of time t is given by
A $\frac{1}{2} m \frac{v}{t_{1}} t^{2}$
B $m \frac{v}{t_{1}} t^{2}$
C $\frac{1}{2} {(\frac{m v}{t_{1}})}^{2} t^{2}$
D $\frac{1}{2} m \frac{v^{2}}{t_{1}^{2}} t^{2}$

GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Objective Questions

Home
Ask Doubt
Profile