In LR circuit, f = 50 Hz, L= 2 H, ε=5V,R=1Ω, then the energy stored in the inductor is:
25 J
50 J
100 J
None of these
The correct Answer is:D
To find the energy stored in the inductor of an LR circuit, we can follow these steps:
Step 1: Identify the given values
- Frequency (f) = 50 Hz
- Inductance (L) = 2 H
- EMF (ε) = 5 V
- Resistance (R) = 1 Ω
Step 2: Calculate the angular frequency (ω)
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100πrad/s
Step 3: Calculate the inductive reactance (X_L)
The inductive reactance (X_L) is calculated using the formula:
XL=ωL
Substituting the values of ω and L:
XL=100π×2=200πΩ
Step 4: Calculate the total impedance (Z)
The total impedance (Z) in an LR circuit is given by:
Z=√R2+X2L
Substituting the values of R and X_L:
Z=√12+(200π)2=√1+40000π2
Step 5: Calculate the current (I)
The current (I) can be calculated using Ohm's law:
I=ϵZ
Substituting the values:
I=5√1+40000π2
Step 6: Calculate the energy stored in the inductor (U)
The energy stored in the inductor is given by the formula:
U=12LI2
Substituting the values of L and I:
U=12×2×(5√1+40000π2)2
This simplifies to:
U=12×2×251+40000π2=251+40000π2
Step 7: Final Calculation
To find the numerical value, we can substitute π ≈ 3.14:
U≈251+40000×(3.14)2
Calculating 40000×(3.14)2:
40000×9.8596≈394384
Thus:
U≈251+394384≈25394385≈6.35×10−5J
Conclusion
The energy stored in the inductor is approximately 6.35×10−5J.
- Frequency (f) = 50 Hz
- Inductance (L) = 2 H
- EMF (ε) = 5 V
- Resistance (R) = 1 Ω
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100πrad/s
The inductive reactance (X_L) is calculated using the formula:
XL=ωL
Substituting the values of ω and L:
XL=100π×2=200πΩ
The total impedance (Z) in an LR circuit is given by:
Z=√R2+X2L
Substituting the values of R and X_L:
Z=√12+(200π)2=√1+40000π2
The current (I) can be calculated using Ohm's law:
I=ϵZ
Substituting the values:
I=5√1+40000π2
The energy stored in the inductor is given by the formula:
U=12LI2
Substituting the values of L and I:
U=12×2×(5√1+40000π2)2
This simplifies to:
U=12×2×251+40000π2=251+40000π2
To find the numerical value, we can substitute π ≈ 3.14:
U≈251+40000×(3.14)2
Calculating 40000×(3.14)2:
40000×9.8596≈394384
Thus:
U≈251+394384≈25394385≈6.35×10−5J
The energy stored in the inductor is approximately 6.35×10−5J.
Topper's Solved these Questions
- SAMPLE PAPER - 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 8EXERCISE - Section B
24 Videos
- SAMPLE PAPER - 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 8EXERCISE - Section C
6 Videos
- CBSE TERM-1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 1EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 04 (SOLVED)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 04 (SOLVED)EXERCISE - SECTION-C
6 Videos
Similar Questions
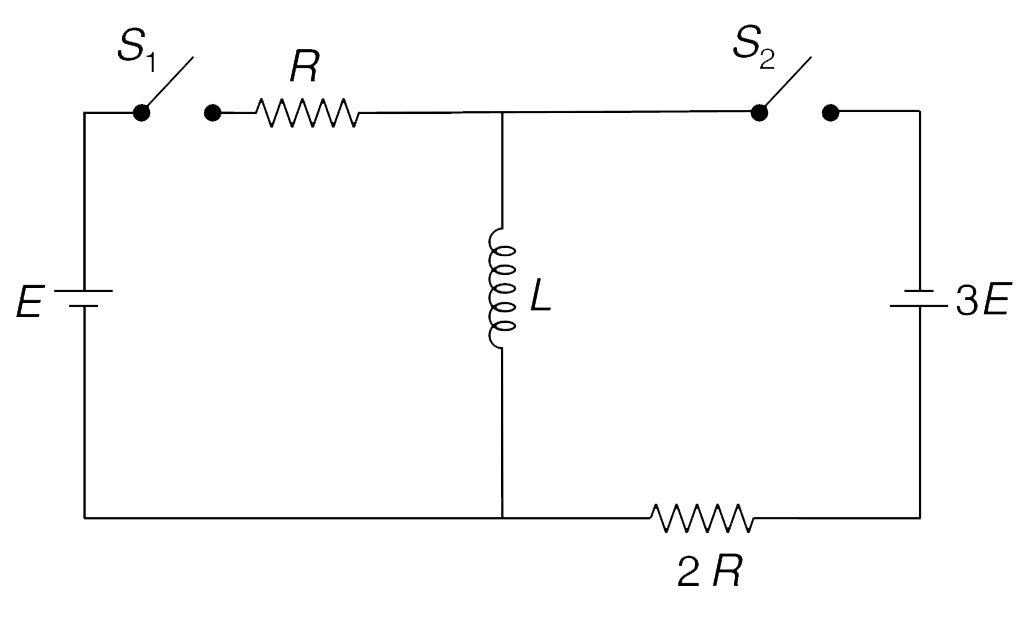
In the circuit shown, switch S2 is open and S1 is closed since long. Take E=20V,L=0.5H and R=10Ω. Find the rate of change of energy stored in the magnetic field inside the inductor, immediately after S2 is closed.
View SolutionAn LR circuit having L=4.0H,R=1.0Ωandε=6.0V is switched on at t=0. find the power dissipated in joule heating at t=4.0s.
View Solution
Knowledge Check
A simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
ARL In [√2√2−1]BLR In [√2−1√2]CLR In [√2√2−1]DRL In [√2−1√2]The battery shown in the figure is ideal.The values are ε=10V,R=5Ω,L=2H Intially the current in the inductor is zero.The current through the battery at t=2s is
 A12AB7AC3ADNone of these
A12AB7AC3ADNone of theseIn a series circuit C=2μF,L=1mH and R=10Ω, when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
A1:1B1:2C2:1D1:5
200 V ac source is fed to series LCR circuit having XL=50Ω,XC=50Ω and R=25Ω. Potential drop across the inductor is
View SolutionAn alternating e.m.f. of 200V,50Hz is applied to a series L-R circuit. If L=0.4π henry and R=30Ω, then the impendance of the circuit and the current in the circuit will be
View SolutionAn LCR circuit contains R=50Ω,L=1mH and C=0.1μF. The impedence of the circuit will be minimum for a frequency of
View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View SolutionAn L-R circuit has R = 10 Ω and L = 2H . If 120 V , 60 Hz AC voltage is applied, then current in the circuit will be
View Solution
