Parallel plate capacitor has capacitance C0=ε0Ad. When a insulating medium is added of dielectric constant K, the capacity becomes Cm=εAd=Kε0Ad=KC0. Let t be the thickness of dielectric such that :
t(<d), then the capacity is Cd=ε0Ad−t(1−1k). For metals, K=∞. Therefore, when a metal plate of thickness t<d is inctroduced, the capacity becomes C=ε0Ad−t.
If the distance between two parallel plates is doubled and area of the plates is halved, the capacitance increases by :
4
1
2
14
The correct Answer is:D
As C0=ε0Ad
∴C.0=ε0A22d=ε0A4d
=14C0
=nC0
⇒n=14
Topper's Solved these Questions
- SAMPLE PAPER - 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 8EXERCISE - Section B
24 Videos
- CBSE TERM-1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 1EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 04 (SOLVED)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 04 (SOLVED)EXERCISE - SECTION-C
6 Videos
Similar Questions
In a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance.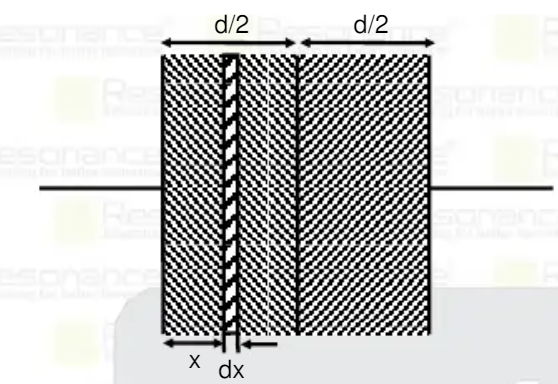
View SolutionIf C and C0 are capacities of a capacitor with and " without dielectric medium respectively then dielectric constant of medium K is
View Solution
Knowledge Check
Parallel plate capacitor has capacitance C0=ε0Ad. When a insulating medium is added of dielectric constant K, the capacity becomes Cm=εAd=Kε0Ad=KC0. Let t be the thickness of dielectric such that :
t(<d), then the capacity is Cd=ε0Ad−t(1−1k). For metals, K=∞. Therefore, when a metal plate of thickness t<d is inctroduced, the capacity becomes C=ε0Ad−t.
Which material will increase the capacitance of a capacitor :AZincBAluminiumCCopperDMicaParallel plate capacitor has capacitance C0=ε0Ad. When a insulating medium is added of dielectric constant K, the capacity becomes Cm=εAd=Kε0Ad=KC0. Let t be the thickness of dielectric such that :
t(<d), then the capacity is Cd=ε0Ad−t(1−1k). For metals, K=∞. Therefore, when a metal plate of thickness t<d is inctroduced, the capacity becomes C=ε0Ad−t.
By introducing a thin foil between the plates of an air capacitor, the capacitance changes by :A3CBC2CCD2CParallel plate capacitor has capacitance C0=ε0Ad. When a insulating medium is added of dielectric constant K, the capacity becomes Cm=εAd=Kε0Ad=KC0. Let t be the thickness of dielectric such that :
t(<d), then the capacity is Cd=ε0Ad−t(1−1k). For metals, K=∞. Therefore, when a metal plate of thickness t<d is inctroduced, the capacity becomes C=ε0Ad−t.
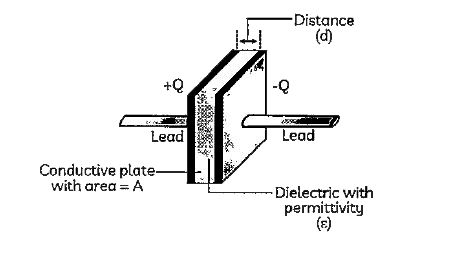
In a capacitor, a metal plate of thickness t=d2 is introduced. The increase in its capacity is :A50%B100%C200%D1%
A parallel plate capacitor has a capacity c. If a medium of dielectric constant K is introduced between plates, the capacity of capacitor becomes
View SolutionA parallel plate capacitor has capacitance C. If it is equally filled with parallel layers of materials of dielectric constants K1 and K2 its capacity becomes C1. The ratio of C1→C is
View SolutionIn vacuum, a parallel plate capacitor has capacitance C0. New capacitance of sheet of thickness t and relative permittivity k is introduced between the plates is (take t=d):
View SolutionA parallel plate condenser with air as dielectric has capacity C0=∈0Ad. A thin mica sheet of dielectric constant K and thickness t is introduced near the first plate and then moved with constant velocity v towards the other plate. The capacity of the condenser will be
View SolutionIf K is the dielectric constant of the medium. A is area of insulated charged plates and d is the distance between two plates of parallel plate condenser then its capacity in CGS unit is
View Solution
