In one observation, the column in a mercury barometer (as is shown in Fig. ) has a measured height h of 740.35 mm. The temperature is −5.0∘ C, at which temperature the density of mercury ρ is 1.3608×104kg/m3 . The free-fall acceleration g at the site of the barometer is 9.7828 m/s2. What is the atmospheric pressure at thal site in pascals and in torr (which is the common unit for barometer readings)?
739.21 torr
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)48videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )10videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT8videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
Knowledge Check
- Question 1 - Select One
The height of mercury barometer is h when the atmospheic pressure is 105Pa. The pressure at x in the shown diagram is
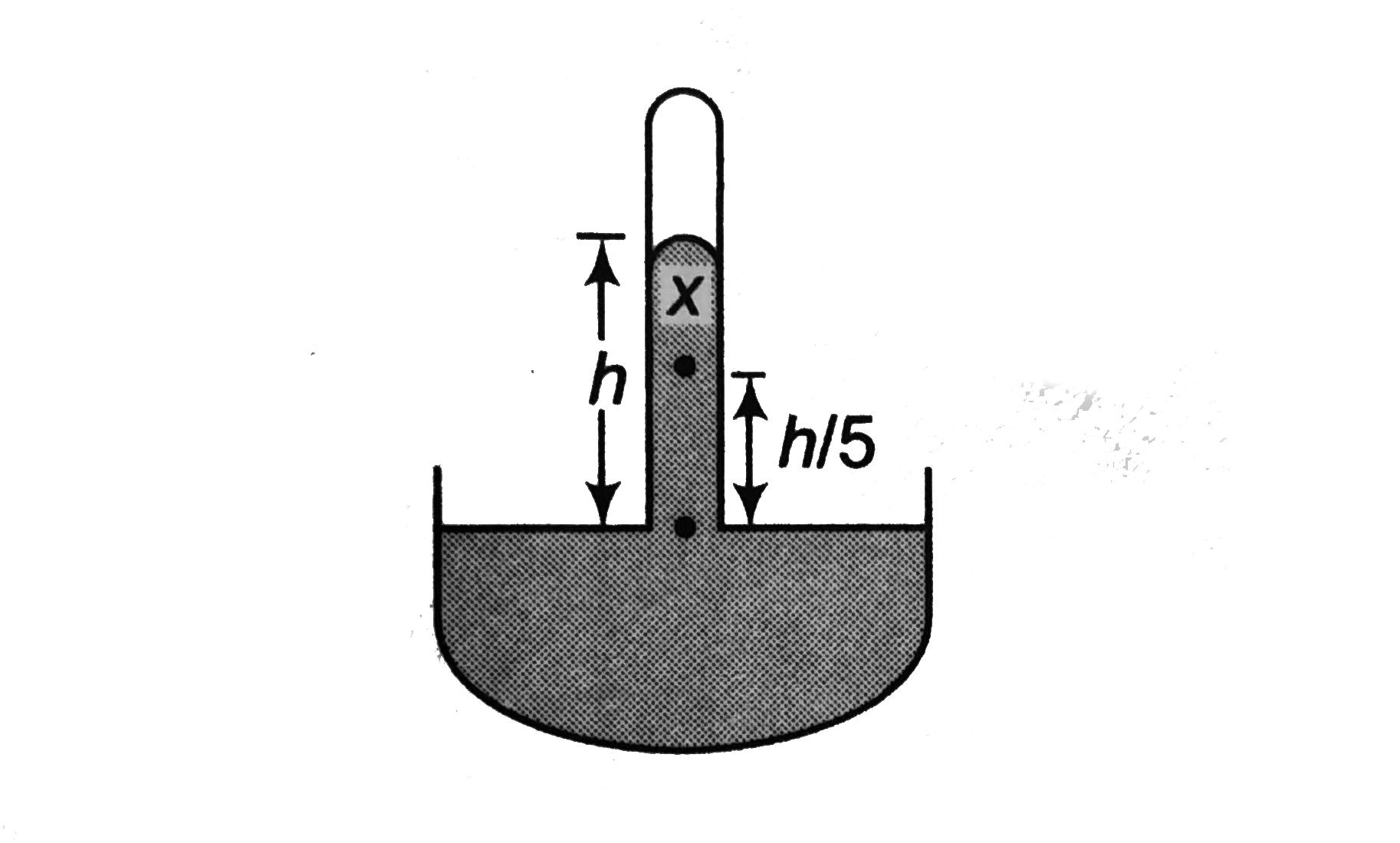 A105PaB0.8×105PaC0.2×105PaD120×105Pa
A105PaB0.8×105PaC0.2×105PaD120×105Pa
Why mercury is used in barometer for measuring atmospheric pressure?
View SolutionExplain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.
View SolutionThe height of mercury barometer is h when the atmospheic pressure is 105Pa. The pressure at x in the shown diagram is
 View Solution
View SolutionMeasuring Pressure By Mercury Barometer
View SolutionCalculate the atmospheric pressure , if the height of mercury column in a barometer is 760 mm
View SolutionThe column of mercury in a barometer is 76 cm Hg. Calculate the atmosphere pressure I the density of mercury =13600kgm−3
(Take g=10ms−2)View SolutionThe column of mercury in a barometer is 76mm of Hg. Calculate the atmospheric pressure if the density of mercury = 13600kgm −3 . (Take g=10ms −2 )
View Solution

