A pitot tube (see Problem 46) on a high-altitude aircraft measures a differential pressure of 150 Pa. What is the air craft's airspeed if the density of the air is 0.031kg/m3 ?
To find the airspeed of the aircraft using the differential pressure measured by the pitot tube, we can apply Bernoulli's equation. Here’s the step-by-step solution:
Step 1: Understand the Problem
The pitot tube measures a differential pressure of 150 Pa, and the density of air is given as 0.031 kg/m³. We need to find the airspeed of the aircraft.
Step 2: Apply Bernoulli's Equation
For a pitot tube, we can use the simplified form of Bernoulli’s equation that relates the pressure difference to the velocity of the fluid (air in this case).
The equation can be expressed as:
ΔP=12ρv2
where:
- ΔP is the differential pressure (150 Pa),
- ρ is the density of air (0.031 kg/m³),
- v is the velocity of the aircraft (what we want to find).
Step 3: Rearranging the Equation
We can rearrange the equation to solve for v:
v2=2ΔPρ
Taking the square root of both sides gives:
v=√2ΔPρ
Step 4: Substitute the Values
Now we substitute the known values into the equation:
v=√2×150Pa0.031kg/m3
Step 5: Calculate the Velocity
First, calculate the numerator:
2×150=300Pa
Now, divide by the density:
3000.031≈9677.42
Now take the square root:
v=√9677.42≈98.4m/s
Final Answer
The airspeed of the aircraft is approximately 98.4 m/s.
---
The pitot tube measures a differential pressure of 150 Pa, and the density of air is given as 0.031 kg/m³. We need to find the airspeed of the aircraft.
For a pitot tube, we can use the simplified form of Bernoulli’s equation that relates the pressure difference to the velocity of the fluid (air in this case).
ΔP=12ρv2
where:
- ΔP is the differential pressure (150 Pa),
- ρ is the density of air (0.031 kg/m³),
- v is the velocity of the aircraft (what we want to find).
We can rearrange the equation to solve for v:
v2=2ΔPρ
Taking the square root of both sides gives:
v=√2ΔPρ
Now we substitute the known values into the equation:
v=√2×150Pa0.031kg/m3
First, calculate the numerator:
2×150=300Pa
3000.031≈9677.42
v=√9677.42≈98.4m/s
The airspeed of the aircraft is approximately 98.4 m/s.
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
48 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
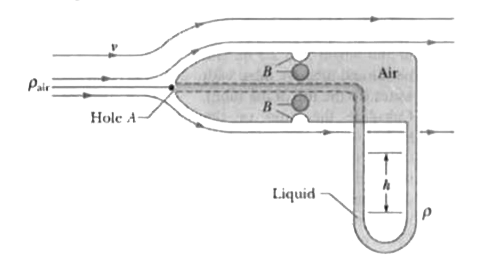
A pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that vA = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
v=√2ρghρair
where ρ is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is 1.03kg/m3 and that of alcohol is 810 kg/m3
View SolutionWhat is the mass of air in a room of dimensions 3m×4m×5m, when the density of air is 1.3 kg m−3?
View Solution
Knowledge Check
What is the height of air column which will produce a pressure of 1 atm? Density of air is 1.3 kg/m3.
A6.45 kmB7.20 kmC7.95 kmD8.40 kmA canister containing 150 kg of an ideal gas has a volume of 8.0 m'. If the gas exerts a pressure of 5.0×105 Pa, what is the rms speed of the molecules?
A160 m/sB282 m/sC350 m/sD390 m/s
A point tube is mounted on an aeroplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm. What is the speed of the plane reative to air ? (sp. Gr. Of alcohol = 0.8 and density of air = 1 kg m−3).
View SolutionA fully loaded Boeing aircraft has a mass of 3.3×105kg. Its total wing area is 500m2 . It is in level flight with a speed of 960km/h.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fracitional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is 1.2kg/m3.
View SolutionThe maximum pressure amplitude Δpm that the human ear can tolerate in loud sounds is about 28 Pa (which is very much less than the normal air pressure of about 105 Pa). What is the displacement amplitude smfor such a sound in air of density ρ=1.21kg/m3, at a frequency of 1000 Hz and a speed of 343 m/s?
View SolutionA note of frequency 300 Hz has an intensity of 1 microwatt per square metre. What is the amplitude of the air vibrations caused by this sound ? (Density of air =1.293kgm−3 and velocity of sound in air =332ms−1)
View SolutionThe figure shows a crude type of perfume atomizer. When bulb at A is compressed, air flows swifty through the tiny BC with uniform speed v, there by causing a reduced pressure at the position of verticall tube DE. The liquid of density 500kg/m3, then rises in the tube, enters tube BC and sprayed out. When bulb is in natural position the air in the bulb and tube are at atmospheric pressure P50=15N/m2. When bulb A is compressed, it creates an exces pressure Δp=0.001P0 inside the bulb A. Density of air is 1.3kg/m3. If the magnitude of minimum value of speed v required to cause the liquid to rise to tube BC is 5km/s. Find the value of k. (g=10m/s2)

View SolutionA typical loud sound wave with a frequency of 1KhZ has a pressure amplitude of about 10 Pa
(a) At t=0, the pressure is a maximum at some point X1. What is the displacement at that point at t=0?
(b) What is the maximum value of the displacement at any time and place/ Take the density of air to be 1.29kg/m3 and speed of sound in air is 340m/s.
View Solution
