In part a of Fig , a surfer rides on the front side of a wave , at a point where a tangent to the wave has a slope of θ=30.0∘ . The combined mass of surfer and surfboard is m = 83.0 kg , and the board has a submerged volume of V=2.50×10−2m3 . The surfer maintains his position on the wave as the wave moves at constant speed toward shore . What is the magnitude and direction (relative to the positive direction of the x-axis in part b of Fig) of the drag force on the surfboard from the water ?
To solve the problem, we will follow these steps:
Step 1: Understanding the Forces Acting on the Surfboard
The forces acting on the surfboard include:
- The buoyant force (upward)
- The weight of the surfer and surfboard (downward)
- The drag force (acting in the direction opposite to the motion of the wave)
Step 2: Calculate the Buoyant Force
The buoyant force (Fb) can be calculated using the formula:
Fb=ρ⋅V⋅g
where:
- ρ = density of seawater = 1.02×103kg/m3
- V = submerged volume = 2.50×10−2m3
- g = acceleration due to gravity = 9.8m/s2
Substituting the values:
Fb=1.02×103kg/m3×2.50×10−2m3×9.8m/s2
Fb=2.509×102N≈250.9N
Step 3: Analyze Forces in the Y-Direction
In the y-direction, we have:
Fb+FDy=mgcos(θ)
where:
- m = mass = 83.0kg
- g = 9.8m/s2
- θ=30∘
Calculating mgcos(30∘):
mg=83.0×9.8≈813.4N
mgcos(30∘)=813.4×√32≈705.4N
Now, substituting into the equation:
250.9+FDy=705.4
FDy=705.4−250.9≈454.5N
Step 4: Analyze Forces in the X-Direction
In the x-direction:
FDx=mgsin(θ)
Calculating mgsin(30∘):
mgsin(30∘)=813.4×12≈406.7N
Step 5: Calculate the Magnitude of the Drag Force
The magnitude of the drag force FD can be calculated using the Pythagorean theorem:
FD=√F2Dx+F2Dy
Substituting the values:
FD=√(406.7)2+(454.5)2
FD=√165396.89+206558.25≈√371955.14≈609.1N
Step 6: Calculate the Direction of the Drag Force
The direction ϕ of the drag force relative to the positive x-axis can be found using:
tan(ϕ)=FDyFDx
Calculating:
tan(ϕ)=454.5406.7
ϕ=tan−1(454.5406.7)≈48.1∘
Final Answer
The magnitude of the drag force on the surfboard is approximately 609.1N and it acts at an angle of 48.1∘ relative to the positive x-axis.
---
The forces acting on the surfboard include:
- The buoyant force (upward)
- The weight of the surfer and surfboard (downward)
- The drag force (acting in the direction opposite to the motion of the wave)
The buoyant force (Fb) can be calculated using the formula:
Fb=ρ⋅V⋅g
where:
- ρ = density of seawater = 1.02×103kg/m3
- V = submerged volume = 2.50×10−2m3
- g = acceleration due to gravity = 9.8m/s2
Fb=1.02×103kg/m3×2.50×10−2m3×9.8m/s2
Fb=2.509×102N≈250.9N
In the y-direction, we have:
Fb+FDy=mgcos(θ)
where:
- m = mass = 83.0kg
- g = 9.8m/s2
- θ=30∘
mg=83.0×9.8≈813.4N
mgcos(30∘)=813.4×√32≈705.4N
250.9+FDy=705.4
FDy=705.4−250.9≈454.5N
In the x-direction:
FDx=mgsin(θ)
Calculating mgsin(30∘):
mgsin(30∘)=813.4×12≈406.7N
The magnitude of the drag force FD can be calculated using the Pythagorean theorem:
FD=√F2Dx+F2Dy
Substituting the values:
FD=√(406.7)2+(454.5)2
FD=√165396.89+206558.25≈√371955.14≈609.1N
The direction ϕ of the drag force relative to the positive x-axis can be found using:
tan(ϕ)=FDyFDx
Calculating:
tan(ϕ)=454.5406.7
ϕ=tan−1(454.5406.7)≈48.1∘
The magnitude of the drag force on the surfboard is approximately 609.1N and it acts at an angle of 48.1∘ relative to the positive x-axis.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.061videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.071videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.041videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
A steel wire 0.72 m long has a mass of 5.0×10−3 kg . If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?
View SolutionThe standing wave pattern shown in the tube has a wave speed of 5.0ms−1. What is the frequency of the standing wave [ in Hz approx.] ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The equation of simple harmonic progressive wave, having amplitude 5×10−2m, wavelength 30 cm, speed 50 m/s and travelling along the positive direction of the x-axis is given by
Ay=0.05sin2π0.3[50t−x]By=0.05sin2π[50t0.3+x0.3]Cy=0.05sinπ0.3(50t−x)Dy=0.05sin100π0.3[t−xλ] - Question 2 - Select One
A transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
Ay(x,t)=0.5sin(2πx−4πt)By(x,t)=0.5cos(2πx+4πt)Cy(x,t)=0.5sin(πx+2πt)Dy(x,t)=0.5cos(2πx+2πt) - Question 3 - Select One
A sound source emits sound waves of frequency 500 Hz and wavelength 0.2 m. How long does it take the waves to travel 300 m.
A75 sB60 sC12 sD3 s
For the wave shown in figure, write the equation of this wave if its position is shown at t=0. Speed of wave is v=300m/s.
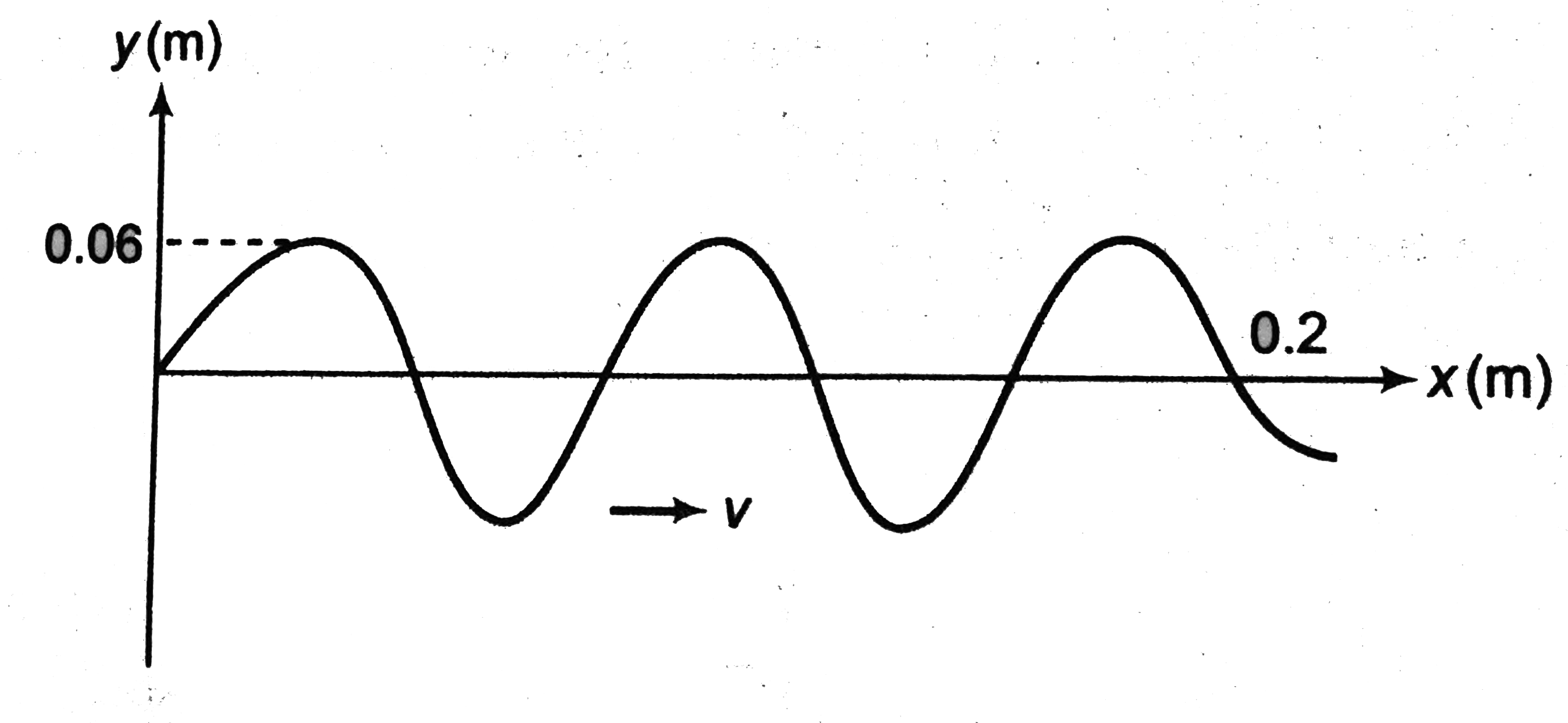 View Solution
View SolutionA transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
View SolutionA wave along a string has the equation y=0.02sin(30t−4x), where x and y are in m and t in second the amplitude of the wave is
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 360m/sec if λ=60m, then correct exression for the wave is
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 36m/sec if λ=60m, then correct expression for the wave is
View Solution

