In perfectily inelastaic collition the relative velocity of the bodies

Topper's Solved these Questions

BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts
32videos
WORK, ENERGY, POWER AND COLLISION
BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17videos
WORK, ENERGY, POWER AND COLLISION
BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21videos
WORK, ENERGY, POWER AND COLLISION
BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30videos
WAVES AND ACOUSTICS

Knowledge Check

Question 1 - Select One
The ratio of relative velocity of separation after collision to the relative velocity of approach before collision between two colliding bodies is ____________.
Acoefficient of restitution
Bvelocity of collision
Csum of the velocities
Dthe law of gravitation
Question 2 - Select One
The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If ${\to v}_{A}$ is the absolute velocity of a body A and $\to - - - (B)$ that of another body B then the relative velocity of A in relation to B is $\to - - - (A D) = {\to V}_{A} - {\to v}_{B}$ and ${\to v}_{B A} = {\to v}_{B}$ - ${\to v}_{A}$ .
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is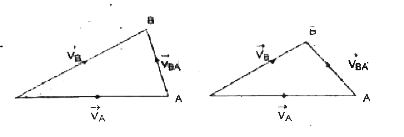
A70 km/hr towards East
B10 km/hr towards North East
C50 km/hr at some angle South of East
D50 km/hr at some angle North of East.
Question 3 - Select One
The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If ${\to v}_{A}$ is the absolute velocity of a body A and $\to - - - (B)$ that of another body B then the relative velocity of A in relation to B is $\to - - - (A D) = {\to V}_{A} - {\to v}_{B}$ and ${\to v}_{B A} = {\to v}_{B}$ - ${\to v}_{A}$ .
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river, capable of swimming at 10 m/s in still water, wants to cross the river without drifting, he. should swim
Adue north
B $30^{\circ}$ east of north
C $30^{\circ}$ west of north
D $60^{\circ}$ east of north

In perfectily inelastaic collition the relative velocity of the bodies

The correct Answer is:C

As in a perfectly inelastic collision, two bodies stick together after the collision and move with same velocity , so their releative velocity after the impact is zero.

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ratio of relative velocity of separation after collision to the relative velocity of approach before collision between two colliding bodies is ____________.

A2Z-WORK, ENERGY, POWER AND COLLISION-Collision