A mass 'm' moves with a velocity 'v' and collides inelastieally with another identical mass . After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision.
⋅→mbeforecollision⋅m↑⏐
⏐
⏐
⏐⏐v/√3aftercollision⟩
2√3v
v√3
v
√3v
The correct Answer is:A
Let mass A moves with velocity v and collides inelastically with mass B, which is at rest.
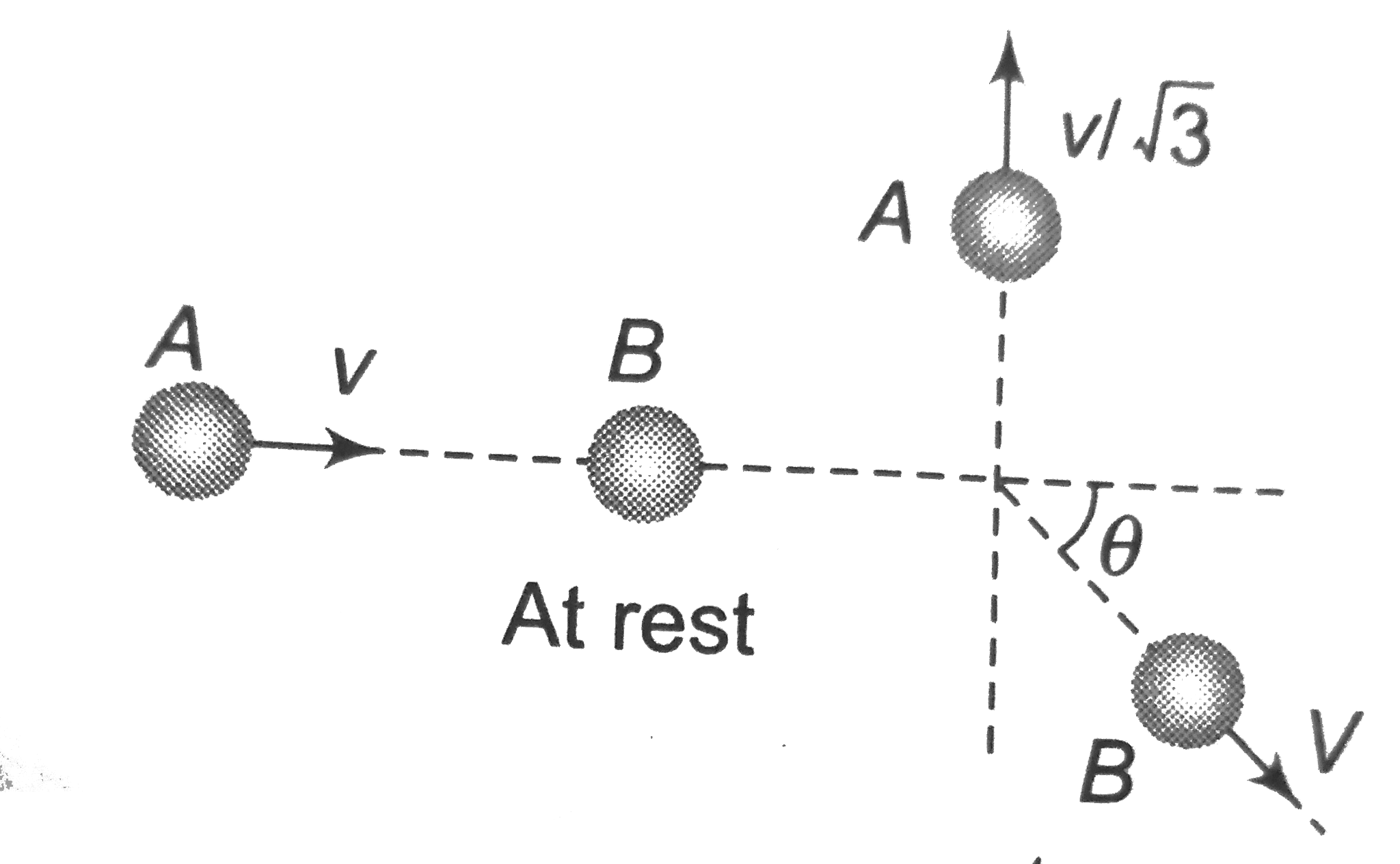
According to problem mass A moves in a perpendicular direction and let the mass B moves at angle θ with the horizontal with velocity v.
Initical horizontal momentum of system
(before collision) =mv (i)
Final horizontal momentum of system
(after collision) = mVcosθ (ii)
From the conservation of horizontal linear momentum
mv=mVcosθ⇒Vcosθ (iii)
Initial vertical momentum of system (bsfore collision) is zero.
Final vertical momentum of system mv√3−mvsinθ
From the conservation of vertical linear momentum
mv√3−mVsinθ=0⇒v√3=Vsinθ (iv)
By solving (iii) and (iv)
v2+v23=V2(sin2θ+cos2θ)
⇒4v23=V2⇒V=2√3v.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View Solution
Knowledge Check
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3A mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
AvB√3vC2√3 vDv√3A mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
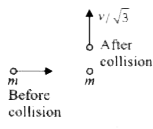 A2v√3Bv√3CvD√3v
A2v√3Bv√3CvD√3v
A sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
View SolutionA ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View Solution