In single slit diffraction pattern, why is intensity of secondary maximum less than the intensity of central maximum ?
To understand why the intensity of secondary maxima in a single slit diffraction pattern is less than the intensity of the central maximum, we can analyze the phenomenon step by step.
1. Understanding Diffraction:
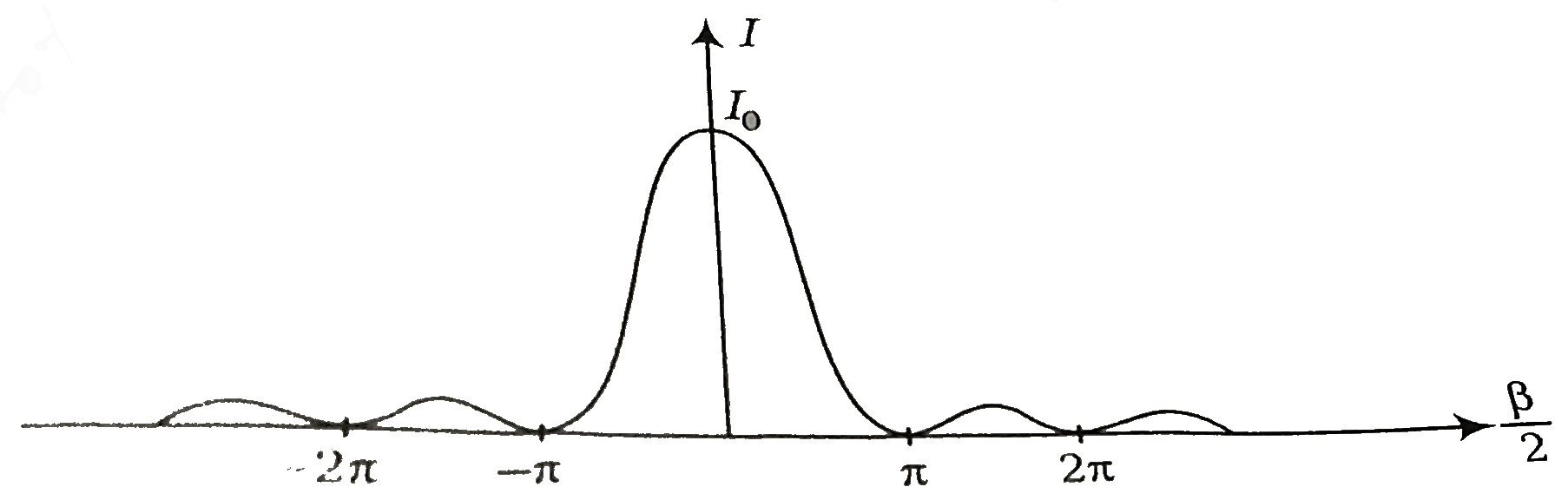
- When light passes through a single slit, it spreads out and creates a diffraction pattern on a screen. This pattern consists of a central maximum (brightest point) and several secondary maxima (less bright points) on either side.
2. Formation of the Central Maximum:
- The central maximum is formed due to constructive interference of light waves emanating from all parts of the slit. Since all parts of the slit contribute to this maximum, the intensity is at its highest.
3. Formation of Secondary Maxima:
- Secondary maxima are formed when there is constructive interference from fewer parts of the slit. As we move away from the central maximum, the path difference between light waves from different parts of the slit increases.
4. Path Difference and Phase Difference:
- For the secondary maxima, the path difference between waves from the edges of the slit leads to a phase difference. This phase difference is not uniform across the slit, resulting in partial cancellation of some waves.
5. Intensity Calculation:
- The intensity of light is proportional to the square of the amplitude of the resultant wave. Since the amplitude of the resultant wave for secondary maxima is less than that for the central maximum (due to partial cancellation), the intensity of the secondary maxima is lower.
6. Mathematical Representation:
- The intensity I can be represented as I∝A2, where A is the amplitude. For the central maximum, A is maximum, while for secondary maxima, A is reduced due to the interference effects.
7. Conclusion:
- Therefore, the intensity of the secondary maxima is less than that of the central maximum because the constructive interference at these points involves contributions from fewer parts of the slit, leading to a lower resultant amplitude and thus lower intensity.
- When light passes through a single slit, it spreads out and creates a diffraction pattern on a screen. This pattern consists of a central maximum (brightest point) and several secondary maxima (less bright points) on either side.
- The central maximum is formed due to constructive interference of light waves emanating from all parts of the slit. Since all parts of the slit contribute to this maximum, the intensity is at its highest.
- Secondary maxima are formed when there is constructive interference from fewer parts of the slit. As we move away from the central maximum, the path difference between light waves from different parts of the slit increases.
- For the secondary maxima, the path difference between waves from the edges of the slit leads to a phase difference. This phase difference is not uniform across the slit, resulting in partial cancellation of some waves.
- The intensity of light is proportional to the square of the amplitude of the resultant wave. Since the amplitude of the resultant wave for secondary maxima is less than that for the central maximum (due to partial cancellation), the intensity of the secondary maxima is lower.
- The intensity I can be represented as I∝A2, where A is the amplitude. For the central maximum, A is maximum, while for secondary maxima, A is reduced due to the interference effects.
- Therefore, the intensity of the secondary maxima is less than that of the central maximum because the constructive interference at these points involves contributions from fewer parts of the slit, leading to a lower resultant amplitude and thus lower intensity.
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Find the intensities of the first three secondary maxima in the single-slit diffraction pattern, measured relative to the intensity of the central maximum
View SolutionFind the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.
View Solution
Knowledge Check
In a single slit diffraction pattern
ACentral fringe has negligible width than othersBall fringes are of same widthCCentral fringe do not existDcentral fringe is twice as wide as other maximaIn a single slit diffraction pattern intensity and width of fringes are
Aunequal widthBequal widthCequal width and equal intensityDunequal width and unequal intensityIn a single - slit diffraction pattern , the position of first secondary maximum is at 30∘ , then what will be the angular position of second minima ?
Asin−1(2/3)Bsin−1(1)Csin−1(1/2)DNone
In a single slit diffraction pattern, how does the angular width of central maxima change when slit width is decreased
View SolutionIn a single-slit diffraction experiment if the slit width is doubled then intensity of central fringe increases to ____the original intensity.
View SolutionIn a single slit diffraction experiment, the width of the slit is made double its original width. Then the central maximum of the diffraction pattern will become
View SolutionIn single slit diffraction experiment, the width of the central maximum inversely proportional to
View SolutionA single slit Fraunhofer diffraction pattern is formed with white light. For what wavelength of light the third secondary maximum in the diffraction pattern coincides with the secondary maximum in the pattern for red light of wavelength 6500 Å ?
View Solution
