Question

Find the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.

Explanation

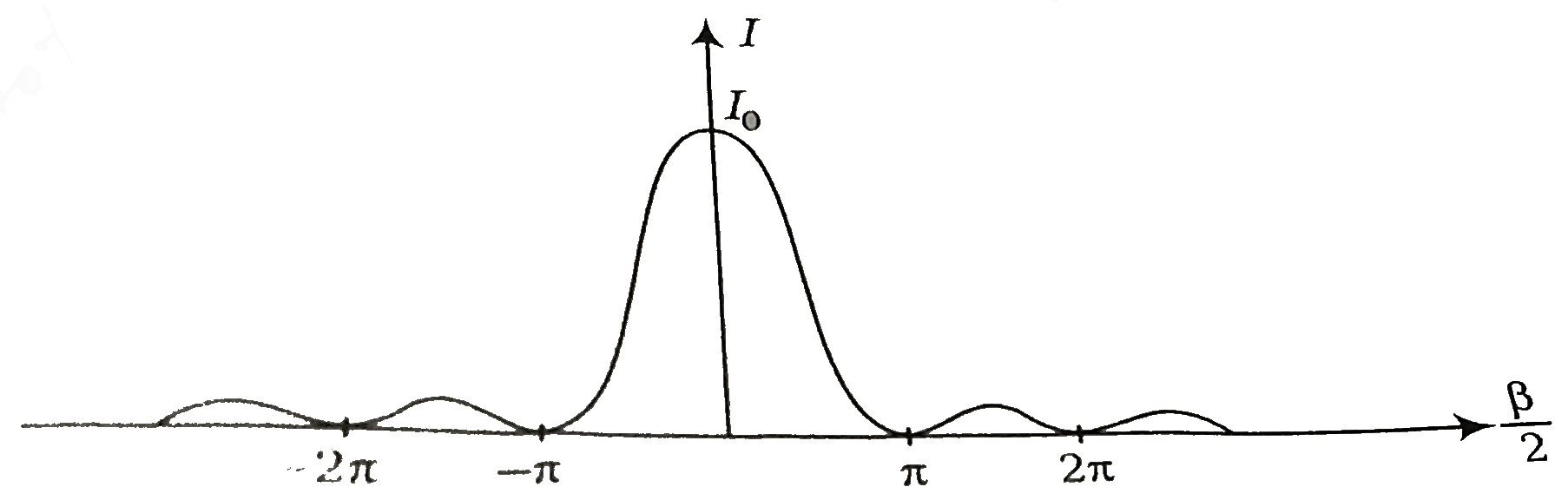
To a good approximation the secondary maxima lie midway between the zero points. From figure we see that this corresponds to `beta//2` values of `3pi//2, 5pi//2, 7pi//2`
`:. I_(1)/I_(0)=[(sin (3pi//2))/((3pi//2))]^(2)=1/(9pi^(2)//4)=0.045`
`I_(2)/I_(0)=[(sin (5pi//2))/(5pi//2)]=1/(25pi^(2)//4)=0.016`
i.e, the first secondary maxima (the ones adjacent to the central maximum) have an intensity of 4.5% that of the central maximum and the next secondary maxima have an intensity of 1.6%that of the central maximum.
Note Secondary maxima does not lie exactly between two minimas.