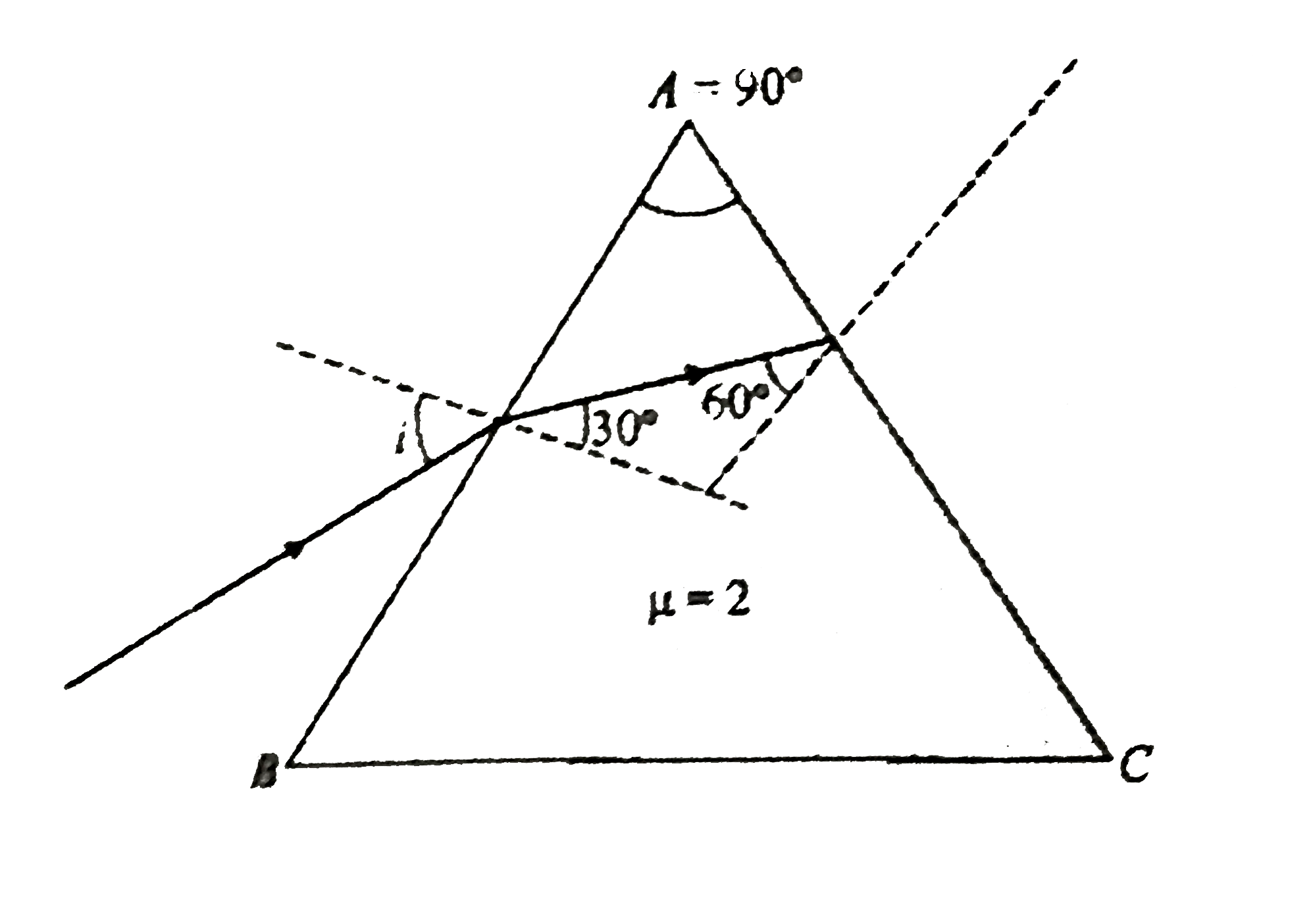
In the above example, find the angle of incidence at face AB, so that emergent ray grazes along the face AC'.
To find the angle of incidence at face AB, so that the emergent ray grazes along the face AC in an equilateral triangle prism with a refractive index of √2, we can follow these steps:
Step 1: Understand the Geometry of the Prism
We have an equilateral triangle prism, where each angle is 60 degrees. The sides are labeled as AB, BC, and AC.
Step 2: Identify the Conditions for Grazing Emergence
For the emergent ray to graze along face AC, it must make an angle of 90 degrees with the normal at that face. This means that the angle of refraction (R2) at face AC will be 90 degrees.
Step 3: Find the Critical Angle
Using the refractive index (μ = √2), we can find the critical angle (C) using the formula:
sinC=1μ
Substituting the value of μ:
sinC=1√2
Thus,
C=45∘
Step 4: Apply the Angle Relation in the Prism
In a prism, the sum of the angles of incidence (R1) and refraction (R2) is equal to the angle of the prism (A):
R1+R2=A
Here, R2 is the critical angle (C = 45 degrees) and A is 60 degrees:
R1+45∘=60∘
From this, we can find R1:
R1=60∘−45∘=15∘
Step 5: Use Snell's Law to Find the Angle of Incidence (I)
Now we can apply Snell's law at face AB:
μsinR1=sinI
Substituting the values we have:
√2sin(15∘)=sinI
Calculating sin(15∘):
sin(15∘)≈0.2588
Thus:
sinI=√2×0.2588
sinI≈0.3659
Step 6: Calculate the Angle of Incidence (I)
Now we find the angle I:
I=sin−1(0.3659)
Calculating this gives:
I≈21.46∘
Final Answer
The angle of incidence at face AB, so that the emergent ray grazes along face AC, is approximately 21.46 degrees.
---
We have an equilateral triangle prism, where each angle is 60 degrees. The sides are labeled as AB, BC, and AC.
For the emergent ray to graze along face AC, it must make an angle of 90 degrees with the normal at that face. This means that the angle of refraction (R2) at face AC will be 90 degrees.
Using the refractive index (μ = √2), we can find the critical angle (C) using the formula:
sinC=1μ
Substituting the value of μ:
sinC=1√2
Thus,
C=45∘
In a prism, the sum of the angles of incidence (R1) and refraction (R2) is equal to the angle of the prism (A):
R1+R2=A
Here, R2 is the critical angle (C = 45 degrees) and A is 60 degrees:
R1+45∘=60∘
From this, we can find R1:
R1=60∘−45∘=15∘
Now we can apply Snell's law at face AB:
μsinR1=sinI
Substituting the values we have:
√2sin(15∘)=sinI
Calculating sin(15∘):
sin(15∘)≈0.2588
Thus:
sinI=√2×0.2588
sinI≈0.3659
Now we find the angle I:
I=sin−1(0.3659)
Calculating this gives:
I≈21.46∘
The angle of incidence at face AB, so that the emergent ray grazes along face AC, is approximately 21.46 degrees.
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Solved Example(d)
32 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Conceptual problem(b)
22 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Solved Example(b)
61 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
In the above example, find the angle of incidence at face AB, so that emergent ray grazes along the face AC'.
View Solution(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
View Solution
Knowledge Check
Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)
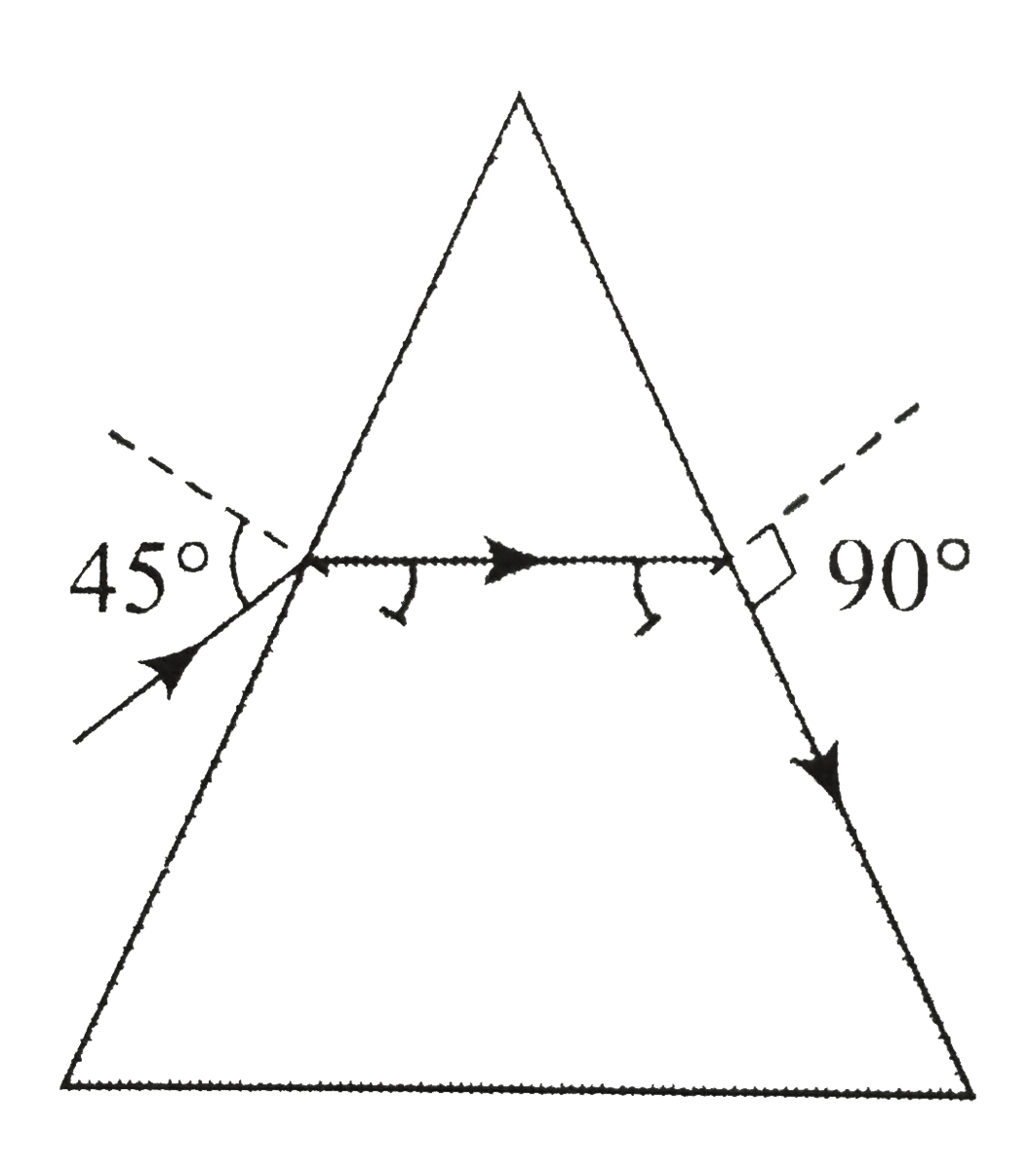
In an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View SolutionIn an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
View SolutionA ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
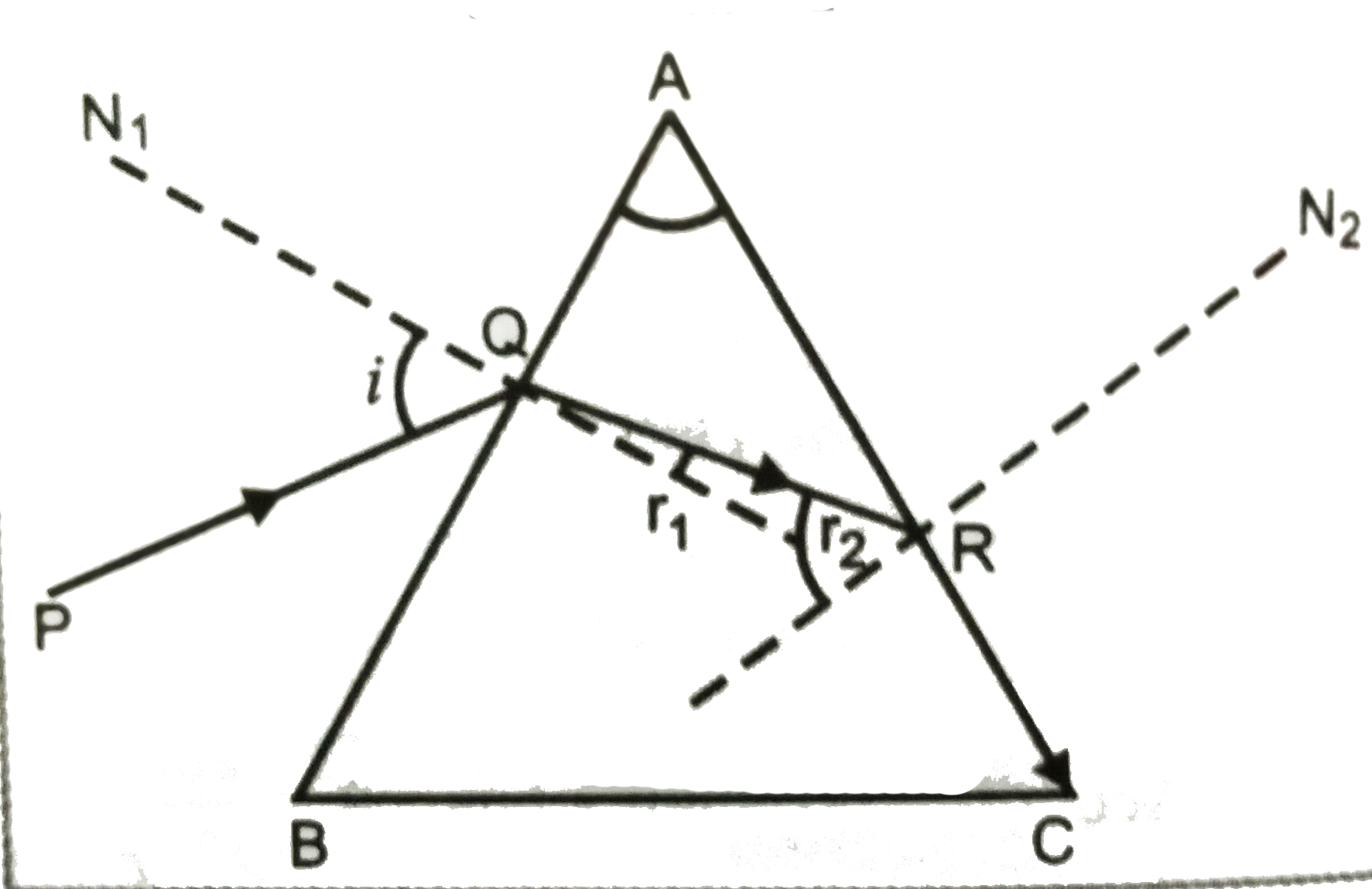
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionIn figure shown find the angle of incidence of the light ray on face AB of the prism for which light will reach face AC at incidence angle 60∘.
[90∘]
View SolutionThe face AC of the prism ABC of refracting angle 30∘ and refractive index square root 2 is silvered. A ray of light, after refraction from face AB, strike the face AC at 90∘. Find the angle of incidence and path traced by the ray after reflecting from the silvered surface.
View Solution
