A ray of light the face of a glass prism of refractive index at an angle of incidence . Find the value of such that no ray emerges from the face of the prism. Given angle of prism is .
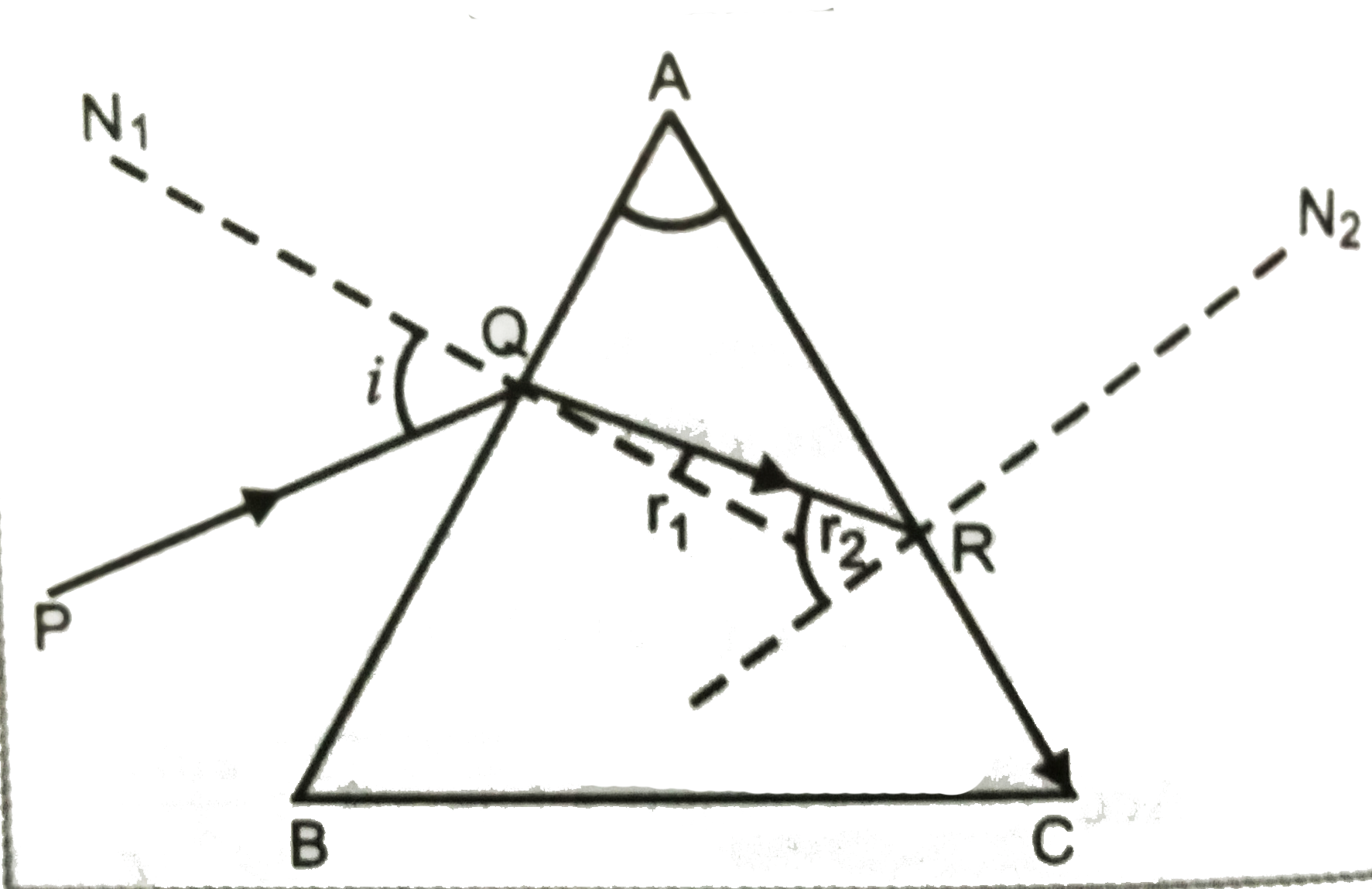
As no ray emerges from face of prism, therefore, refracted ray must be undergoing total internal reflection at .
.
As
. …(i)
...(ii)
but
form (ii),
using (i),
From (i),
From (iii), .
Hence,
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Very short answer question
Explore 5 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:very short answer questions
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
A ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
Knowledge Check
A glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
A60∘B30∘C45∘Dthe ray does not emergeLight falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
A45°B60°C15°D90°Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)
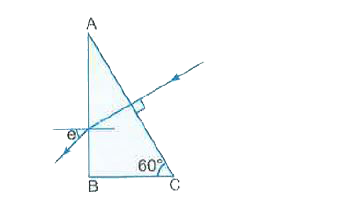
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution