In the above problem, if the battery is disconnected before inserting the dielectric, then difference will be
0.5 V
2 V
4 V
32 V
The correct Answer is:A
To solve the problem step by step, we need to analyze the situation when a dielectric is inserted into a capacitor after the battery has been disconnected.
1. Understand the Initial Setup:
- A capacitor is connected to a battery (4 volts in this case) which charges the capacitor to a certain charge Q.
- When the battery is disconnected, the charge Q on the capacitor remains constant because there is no path for charge to flow.
Hint: Recall that when a battery is connected to a capacitor, it charges up to a voltage equal to the battery voltage.
2. Insert the Dielectric:
- When a dielectric material is inserted between the plates of the capacitor, the capacitance C of the capacitor increases. The new capacitance with the dielectric can be expressed as C′=kC, where k is the dielectric constant.
Hint: Remember that inserting a dielectric increases the capacitance of the capacitor.
3. Relate Charge, Voltage, and Capacitance:
- The relationship between charge Q, capacitance C, and voltage V is given by the formula:
Q=CV
- Since Q is constant (because the battery is disconnected), we can express the new voltage V′ after inserting the dielectric as:
Q=C′V′andQ=CV
- Therefore, we can write:
CV=C′V′
Hint: Use the relationship Q=CV to express how the voltage changes when the capacitance changes.
4. Substituting for Capacitance:
- Substitute C′=kC into the equation:
CV=kCV′
- Dividing both sides by C (assuming C≠0):
V=kV′
- Rearranging gives:
V′=Vk
Hint: Isolate V′ to find how the voltage changes with the dielectric constant.
5. Calculate the New Voltage:
- If the dielectric constant k=8 (as suggested in the video transcript), then:
V′=V8
- Given that the initial voltage V=4 volts, we find:
V′=48=0.5 volts
Hint: Substitute the known values to find the new voltage across the capacitor.
Final Answer:
The new voltage across the capacitor after inserting the dielectric is 0.5 volts.
- A capacitor is connected to a battery (4 volts in this case) which charges the capacitor to a certain charge Q.
- When the battery is disconnected, the charge Q on the capacitor remains constant because there is no path for charge to flow.
- When a dielectric material is inserted between the plates of the capacitor, the capacitance C of the capacitor increases. The new capacitance with the dielectric can be expressed as C′=kC, where k is the dielectric constant.
- The relationship between charge Q, capacitance C, and voltage V is given by the formula:
Q=CV
- Since Q is constant (because the battery is disconnected), we can express the new voltage V′ after inserting the dielectric as:
Q=C′V′andQ=CV
- Therefore, we can write:
CV=C′V′
- Substitute C′=kC into the equation:
CV=kCV′
- Dividing both sides by C (assuming C≠0):
V=kV′
- Rearranging gives:
V′=Vk
- If the dielectric constant k=8 (as suggested in the video transcript), then:
V′=V8
- Given that the initial voltage V=4 volts, we find:
V′=48=0.5 volts
The new voltage across the capacitor after inserting the dielectric is 0.5 volts.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A parallel plate air capacitor is connected to a battery. If the plates of the capacitor are pulled farther apart, then state whether the following statements are true or false.
a. Strength of the electric field inside the capacitor remains unchanged, if the battery is disconnected before pulling the plates.
b. During the process, work is done by the external force applied to pull the plates irrespective of whether the battery is disconnected or not.
c. Strain energy in the capacitor decreases if the battery remains connected.
 .
.
View SolutionIn the above problem, direction of friction force is
View SolutionIn the arrangement shown, the battery is disconnected and a dielectric slab of dielectric constant K is insereted between the plates of capacitor with capacitance C, so as to completely fill the space. What is the final potential differnece across capacitor with capacitance 2C ?
View SolutionThe resonant frequency of L-C circuit is f0 before insertion of dielectric of (dielectric constant) (Er=4). After inserting the dielectric, the resonant frequency will be
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
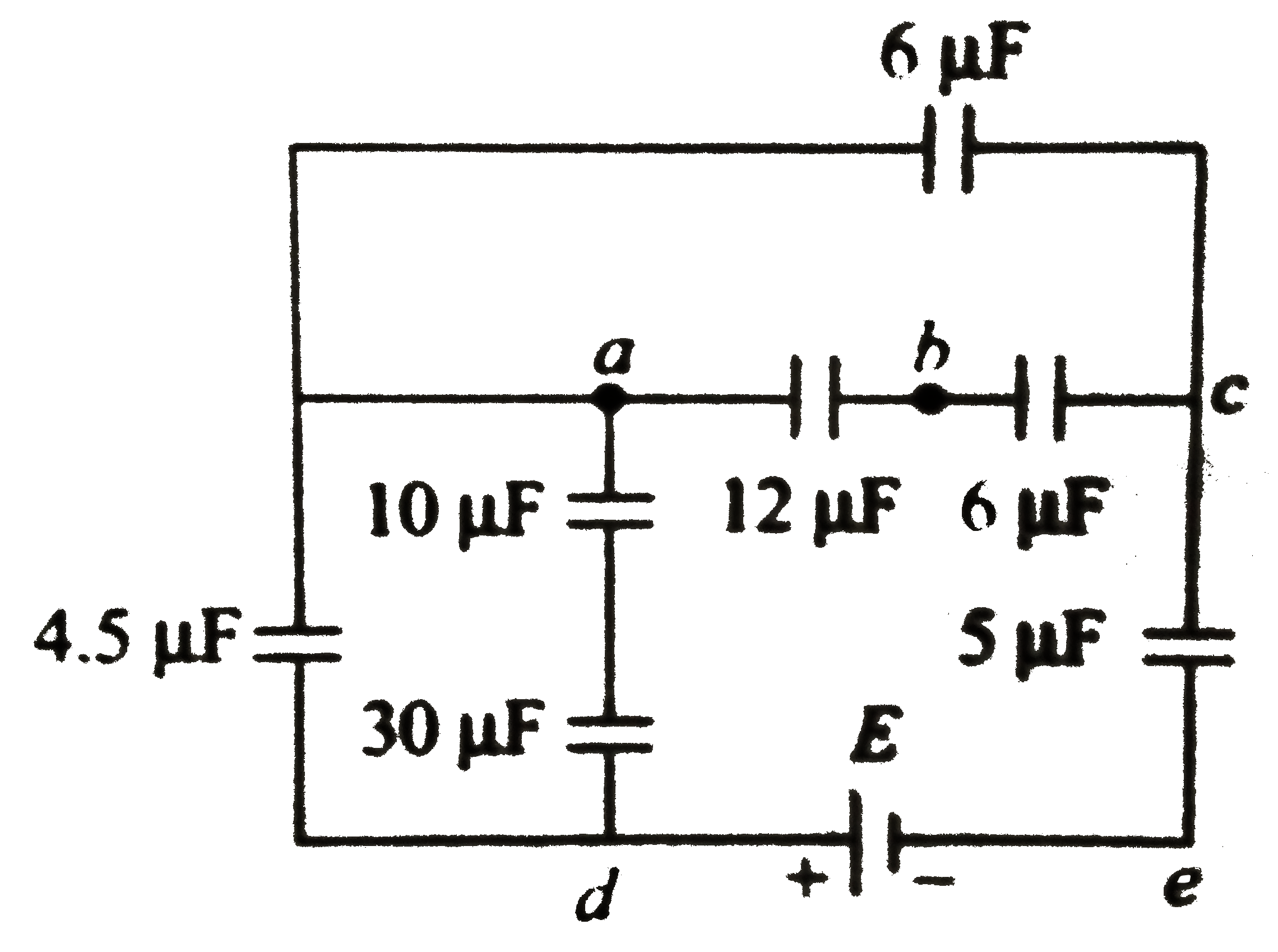
View SolutionIn the circuit shown in the potential difference between the point a and b is 4V, Find the emf ε of the battery. Assume that before connecting the battery in the circuit, all the capacitors were uncharged.
 .
.
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View SolutionA parallel plate capacitor is charged by a battery. After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates. How will (i) the capacitance of the capacitor, (ii) potential difference between the plates and (iii) the energy stored in the capacitor be affected ?
Justify your answer in each case.
View SolutionA capacitor has some dielectric between its plates, and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, electric field, charge stored and the voltage will increase ro remain constant.
View Solution

