In the above problem mass of ice and water in the mixture when thermal equlibrium is attained is
40 g ice, 180 g water
60 g ice, 160 g water
20 g ice, 200 g water
None of the above
The correct Answer is:C
To solve the problem of finding the mass of ice and water in the mixture when thermal equilibrium is attained, we can follow these steps:
Step 1: Understand the Problem
We need to find the mass of ice and water in a mixture at thermal equilibrium. The problem states that the heat exchange occurs until the system reaches thermal equilibrium.
Step 2: Identify the Given Data
- The heat absorbed by the ice to melt and then reach thermal equilibrium is given as 8000 calories.
- The latent heat of fusion of ice (L) is approximately 80 calories/gram.
- The initial mass of ice is 120 grams.
- The initial mass of water is 100 grams.
Step 3: Calculate the Heat Required to Melt the Ice
Using the formula for heat (Q) absorbed during melting:
Q=m⋅L
Where:
- Q = heat absorbed (calories)
- m = mass of ice (grams)
- L = latent heat of fusion (calories/gram)
We can rearrange this to find the mass of ice that can absorb 8000 calories:
8000=m⋅80
m=800080=100 grams
Step 4: Determine the Final Mass of Ice and Water
- Initially, we have 120 grams of ice. After melting 100 grams of ice, we are left with:
Remaining ice=120 grams−100 grams=20 grams
- The water produced from the melted ice will be 100 grams.
- Initially, there was 100 grams of water, so the total mass of water after melting is:
Total water=100 grams (initial)+100 grams (from melted ice)=200 grams
Step 5: Conclusion
At thermal equilibrium, we have:
- Remaining ice = 20 grams
- Total water = 200 grams
Thus, the total mass of the mixture (ice + water) is:
Total mass=20 grams (ice)+200 grams (water)=220 grams
Final Answer
The mass of ice and water in the mixture when thermal equilibrium is attained is 220 grams.
---
We need to find the mass of ice and water in a mixture at thermal equilibrium. The problem states that the heat exchange occurs until the system reaches thermal equilibrium.
- The heat absorbed by the ice to melt and then reach thermal equilibrium is given as 8000 calories.
- The latent heat of fusion of ice (L) is approximately 80 calories/gram.
- The initial mass of ice is 120 grams.
- The initial mass of water is 100 grams.
Using the formula for heat (Q) absorbed during melting:
Q=m⋅L
Where:
- Q = heat absorbed (calories)
- m = mass of ice (grams)
- L = latent heat of fusion (calories/gram)
8000=m⋅80
m=800080=100 grams
- Initially, we have 120 grams of ice. After melting 100 grams of ice, we are left with:
Remaining ice=120 grams−100 grams=20 grams
- The water produced from the melted ice will be 100 grams.
- Initially, there was 100 grams of water, so the total mass of water after melting is:
Total water=100 grams (initial)+100 grams (from melted ice)=200 grams
At thermal equilibrium, we have:
- Remaining ice = 20 grams
- Total water = 200 grams
Total mass=20 grams (ice)+200 grams (water)=220 grams
The mass of ice and water in the mixture when thermal equilibrium is attained is 220 grams.
Topper's Solved these Questions
Similar Questions
A metal piece weighing 15g is heated to 100∘C and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by 0.15cm3 with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice =0.92, specific gravity of water at 0∘C=1.0, latent heat of fusion of ice =80cal−g−1.
View Solution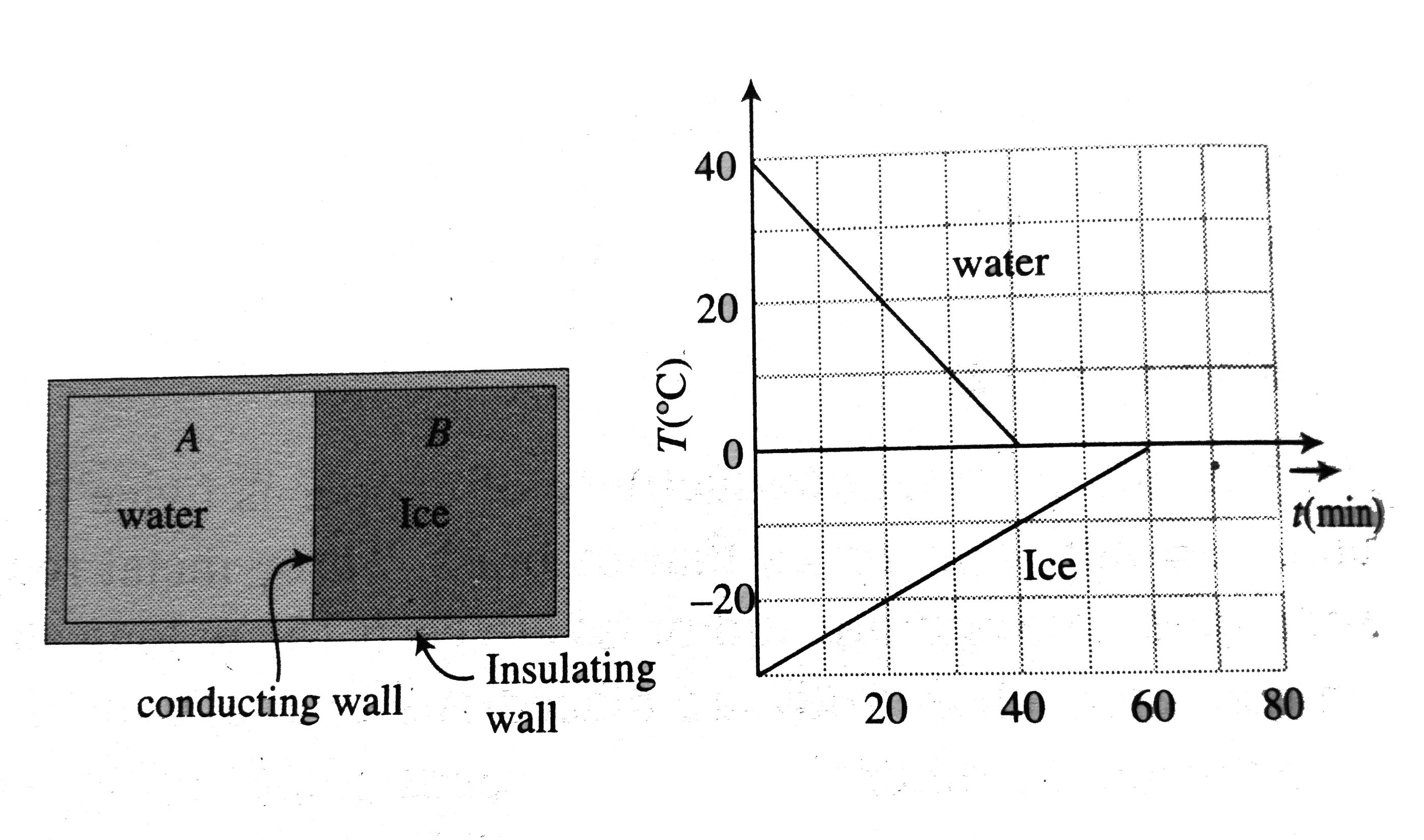
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution
Knowledge Check
Assertion : When ice and water are kept in a perfectly insulated thermos flask at 273 K and the atmospheric pressure, there is no change in mass of ice and water.
Reason : The system is in static equilibrium.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.

A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution4 mole of N2O4 is taken in container of unit volume at any temperature. After some time, equlibrium is attained and vapour density of mixture is 34.5. The value of ΔG will be
View SolutionIf the thickness of the plate in the above problem is 2 mm, find the downward force when plate is placed vertically on water along its longest side.
View Solution50 g ice at 0∘C is dropped into a calorimeter containing 100 g water at 30∘C. If thermal . capacity of calorimeter is zero then amount of ice left in the mixture at equilibrium is
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View SolutionIce has formed on a shallow pond, and a steady state has been reached, with the air above the ice at −5.0∘C and the bottom of the pond at 40∘C. If the total depth of ice + water is 1.4m, (Assume that the thermal conductivities of ice and water are 0.40 and 0.12cal/mC∘s, respectively.)
The thickness of ice layer is
View Solution
