In the above question, if equal forces are applied on two springs, then
(a) More work is done on Q
(b) More work is done on P
(c) Heir force constants will become equal
(d) Equal work is done on both the springs
The correct Answer is:A
To solve the problem step by step, we will analyze the situation with two springs having different spring constants when equal forces are applied to them.
Step 1: Understand the Given Information
We have two springs with spring constants k1 and k2, where k1>k2. When equal forces F are applied to both springs, we need to determine the elongation in each spring.
Hint: Remember that the elongation in a spring is related to the force applied and the spring constant.
Step 2: Apply Hooke's Law
According to Hooke's Law, the force exerted by a spring is given by:
F=k⋅x
where F is the force applied, k is the spring constant, and x is the elongation (displacement) of the spring.
For spring 1:
F=k1⋅x1
For spring 2:
F=k2⋅x2
Hint: Since the forces are equal, we can set the two equations equal to each other.
Step 3: Set the Forces Equal
Since F is the same for both springs:
k1⋅x1=k2⋅x2
Hint: Rearranging this equation will help us find the relationship between x1 and x2.
Step 4: Solve for Elongations
Rearranging the equation gives us:
x1=k2k1⋅x2
Since k1>k2, we can conclude that:
k2k1<1
This means:
x1<x2
Hint: This indicates that the elongation in the spring with the larger spring constant (spring 1) is less than that in the spring with the smaller spring constant (spring 2).
Step 5: Calculate Work Done on Each Spring
The work done on a spring is given by:
W=F⋅x
For spring 1:
W1=F⋅x1
For spring 2:
W2=F⋅x2
Hint: Since x1<x2, the work done on spring 1 will be less than the work done on spring 2.
Step 6: Compare Work Done
Since x1<x2 and the force F is the same for both springs:
W1<W2
Thus, we conclude:
W1<W2
Final Conclusion: More work is done on spring 2 (the one with the smaller spring constant).
Summary of the Answer
The work done on spring 2 (with spring constant k2) is greater than the work done on spring 1 (with spring constant k1).
Final Answer: More work is done on spring 2.
We have two springs with spring constants k1 and k2, where k1>k2. When equal forces F are applied to both springs, we need to determine the elongation in each spring.
According to Hooke's Law, the force exerted by a spring is given by:
F=k⋅x
where F is the force applied, k is the spring constant, and x is the elongation (displacement) of the spring.
F=k1⋅x1
For spring 2:
F=k2⋅x2
Since F is the same for both springs:
k1⋅x1=k2⋅x2
Rearranging the equation gives us:
x1=k2k1⋅x2
k2k1<1
This means:
x1<x2
The work done on a spring is given by:
W=F⋅x
For spring 1:
W1=F⋅x1
For spring 2:
W2=F⋅x2
Since x1<x2 and the force F is the same for both springs:
W1<W2
W1<W2
The work done on spring 2 (with spring constant k2) is greater than the work done on spring 1 (with spring constant k1).
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
In the question number 91, if a force Fis applied to 20 kg block, then the tension in the string is
A100NB200NC300ND400N
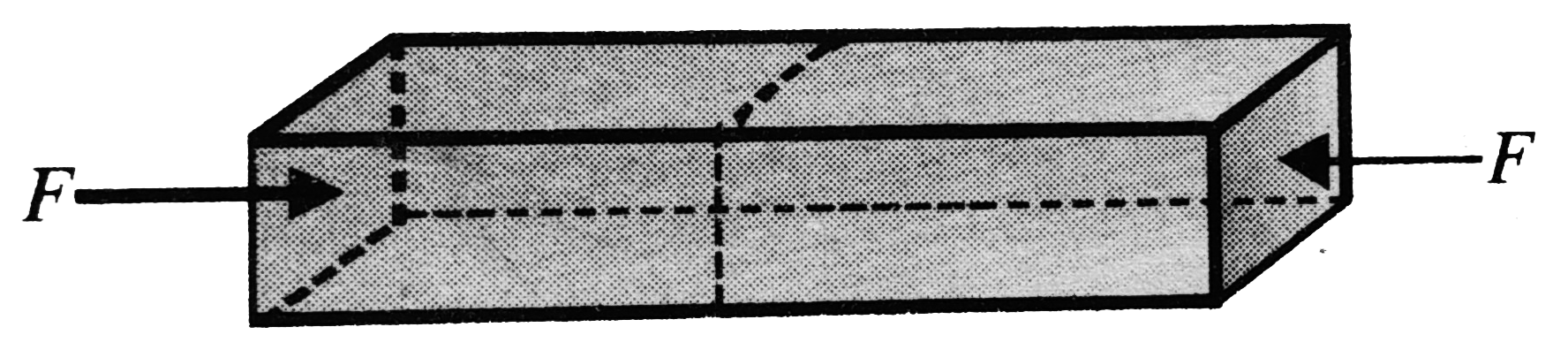
In the figure shown, forces of equal magnitude are applied to the two ends of a uniform rod. Consider A as the cross-sectional area of the rod. For this situation, mark out the incorrect statements.
View SolutionIn the above question, angular displacement of the disc, in first two second will be in radian:
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA vertical spring carries a 5kg body and is hanging in equilibrium an additional force is applied so that the spring is further stretched. When released from this position. It performs 50 complete oscillation in 25 s, with an amplitude of 5 cm. The additional force applied is
View SolutionTwo springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
View SolutionThe length of a spring is α when a force of 4N is applied on it and the length is β when 5N is applied. Then the length of spring when 9N force is applied is-
View SolutionA block of mass m welded with a light spring of stiffness k is in equilibrium on an smooth inclined plane with angle of inclination θ. If a variable external force is applied slowly till the spring comes to its relaxed position, find the work done by spring force.

View Solution
