A vertical spring carries a 5kg body and is hanging in equilibrium an additional force is applied so that the spring is further stretched. When released from this position. It performs 50 complete oscillation in 25 s, with an amplitude of 5 cm. The additional force applied is
80 N
80π2N
4π2N
4N
The correct Answer is:C
To solve the problem step by step, we will follow the concepts of simple harmonic motion and the properties of springs.
Step 1: Calculate the Time Period (T)
The total time for 50 oscillations is given as 25 seconds. Therefore, we can calculate the time period (T) using the formula:
T=Total timeNumber of oscillations=25 s50=0.5 s
Hint: Remember that the time period is the time taken for one complete oscillation.
Step 2: Calculate the Angular Frequency (ω)
The angular frequency (ω) can be calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π0.5=4π rad/s
Hint: Angular frequency relates to the time period and is measured in radians per second.
Step 3: Calculate the Spring Constant (K)
The spring constant (K) can be calculated using the formula:
K=ω2⋅m
Where m is the mass (5 kg):
K=(4π)2⋅5=16π2⋅5=80π2 N/m
Hint: The spring constant relates the force exerted by the spring to the displacement from its equilibrium position.
Step 4: Calculate the Additional Force (F)
The additional force applied to the spring can be calculated using Hooke's Law:
F=K⋅x
Where x is the amplitude of the oscillation (5 cm = 0.05 m):
F=80π2⋅0.05=4π2 N
Hint: Hooke's Law states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position.
Final Answer
The additional force applied is:
F=4π2 N
Summary of Steps
1. Calculate the time period (T).
2. Calculate the angular frequency (ω).
3. Calculate the spring constant (K).
4. Calculate the additional force (F) using Hooke's Law.
The total time for 50 oscillations is given as 25 seconds. Therefore, we can calculate the time period (T) using the formula:
The angular frequency (ω) can be calculated using the formula:
The spring constant (K) can be calculated using the formula:
The additional force applied to the spring can be calculated using Hooke's Law:
The additional force applied is:
1. Calculate the time period (T).
2. Calculate the angular frequency (ω).
3. Calculate the spring constant (K).
4. Calculate the additional force (F) using Hooke's Law.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A vertical spring of force cosntant 100N/m is attached with a hanging mass of 10 kg. Now an external force is applied on the mass so that the spring is stretched by additional 2m. The work done by the force F is (g=10m/s2)
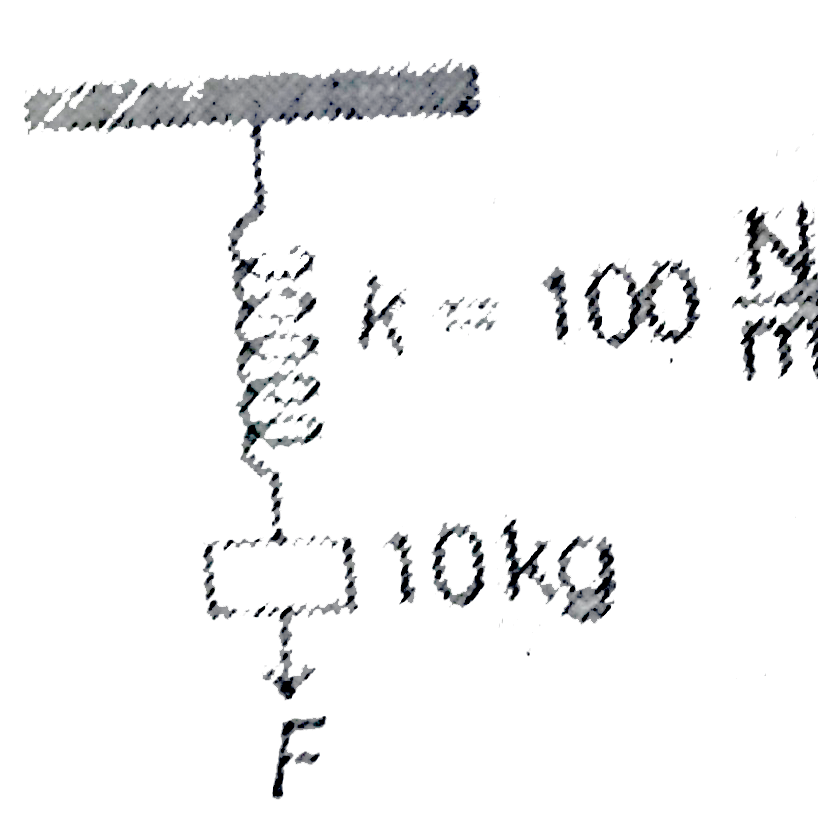
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
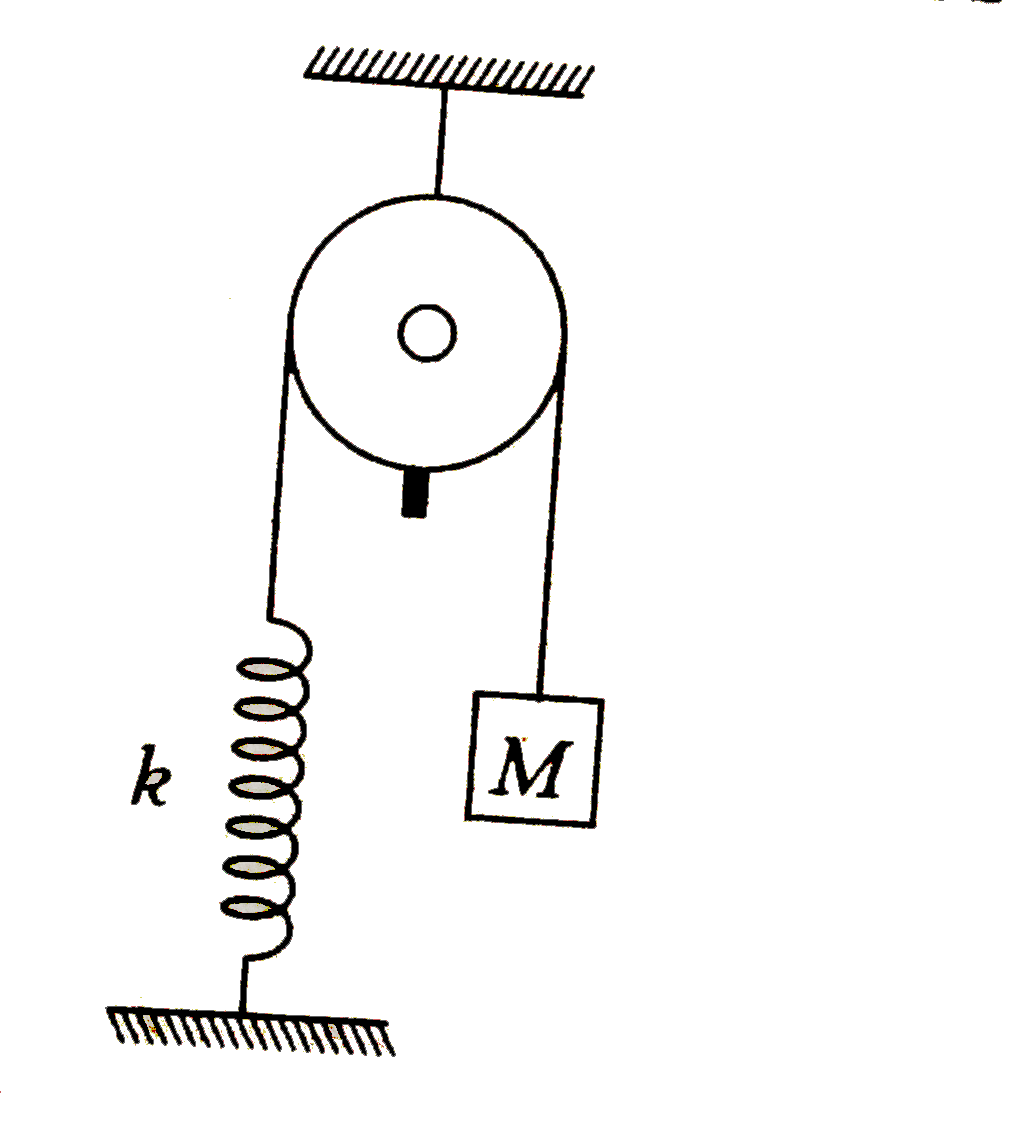
View SolutionThe length of a spring is α when a force of 4N is applied on it and the length is β when 5N is applied. Then the length of spring when 9N force is applied is-
View SolutionA force acts for 0.1 s on a body of mass 2 kg initially at rest. The force is then withdrawn and the body moves with a velocity of 2 m/s. Find the magnitude of force.
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (ρ) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the frequency of oscillation of the cylinder is.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View Solution
