In the above question, if the internal resistance of the battery is 1 ohm , then what is the reading of ammeter
5/3A
40/29A
10/9A
1A
The correct Answer is:B
To find the reading of the ammeter when the internal resistance of the battery is 1 ohm, we will follow these steps:
Step 1: Understand the Circuit
We have a circuit with a 10V battery, a 5-ohm resistor, a 4-ohm resistor, and the internal resistance of the battery is 1 ohm. The total current flowing through the circuit is denoted as I, and the current flowing through the 5-ohm resistor is denoted as I1.
Step 2: Apply Kirchhoff's Voltage Law (KVL) in Loop 1
Using KVL in Loop 1, we can write the equation based on the voltage drops across the resistors:
10V=5I1+1I
This can be rearranged to form our first equation:
10=5I1+I(Equation 1)
Step 3: Apply KVL in Loop 2
Next, we apply KVL in Loop 2, which includes the 5-ohm and 4-ohm resistors:
5I1−4(I−I1)=0
Expanding this gives:
5I1−4I+4I1=0
Combining like terms results in:
9I1=4I
This can be rearranged to form our second equation:
I=94I1(Equation 2)
Step 4: Substitute Equation 2 into Equation 1
Now, we substitute Equation 2 into Equation 1:
10=5I1+94I1
To combine the terms, we convert 5I1 to a fraction:
10=204I1+94I1
This simplifies to:
10=294I1
Step 5: Solve for I1
Now, we can solve for I1:
I1=10×429=4029 A
Step 6: Find the Ammeter Reading
Since the ammeter measures the total current I, we can now substitute I1 back into Equation 2 to find I:
I=94×4029=360116=9029 A
Thus, the reading of the ammeter is:
Ammeter Reading=9029 A
Summary of the Solution
The reading of the ammeter is 9029 A.
---
We have a circuit with a 10V battery, a 5-ohm resistor, a 4-ohm resistor, and the internal resistance of the battery is 1 ohm. The total current flowing through the circuit is denoted as I, and the current flowing through the 5-ohm resistor is denoted as I1.
Using KVL in Loop 1, we can write the equation based on the voltage drops across the resistors:
Next, we apply KVL in Loop 2, which includes the 5-ohm and 4-ohm resistors:
Now, we substitute Equation 2 into Equation 1:
Now, we can solve for I1:
Since the ammeter measures the total current I, we can now substitute I1 back into Equation 2 to find I:
The reading of the ammeter is 9029 A.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Kirchhoff s Law, cells8videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Different Measuring Instruments1videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - COMMUNICATION SYSTEMEXERCISE - S E T14videos
COMMUNICATION SYSTEM
- BOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET20videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
A resistance of 97Ω is connected to a battery of emf 10 V . To measure the current passing in the circuit, an ammeter is inserted in series with the resistance. It is found that the ammeter reads 100 mA. What is the internal resistance of the battery if 2Ω is the resistance of ammeter ?
View SolutionIn Fig. 6.76, the ammeter (I) reads a current of 10mA, while the voltmeter reads a potential difference of 3V. The ammeters are identical, and the internal resistance of the battery is negligible (consider all ammeters and voltmers as nonideal).
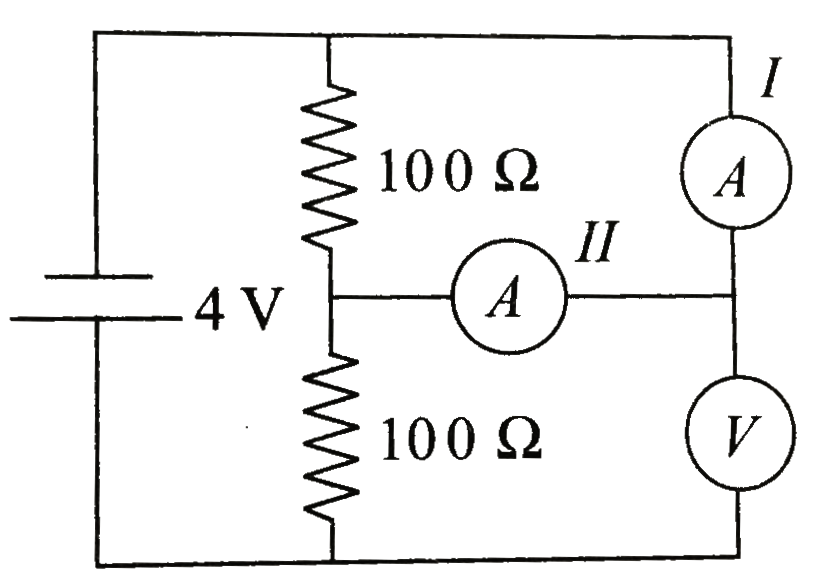
The resistance of ammeter is m×102Ω. What is the value of m ?View Solution
Knowledge Check
- Question 1 - Select One
Two batteries A and B each of e.m.f. 2 V are connected in series to an external resistance R = 1 ohm . If the internal resistance of battery A is 1.9 ohms and that of B is 0.9 ohm , what is the potential difference between the terminals of battery A
 A2VB3.8VCZeroDNone of the above
A2VB3.8VCZeroDNone of the above - Question 2 - Select One
Taking the internal resistance of the battery as negligible, the steady state current in the 2ohm resistor shown in the figure will be
 A1.8 AB2.9 AC0.9 AD2.8 A
A1.8 AB2.9 AC0.9 AD2.8 A - Question 3 - Select One
Taking the internal resistance of the battery as negligible, the steady state current in the 2ohm resistor shown in the figure will be
 A1.8 AB2.9 AC0.9 AD2.8 A
A1.8 AB2.9 AC0.9 AD2.8 A
In the figure ammeter (i) reads a current of 10mA, while the voltmeter reads a potential difference of 3V. What does ammeter (ii) (in mA) read? The ammeters are identical, the internal resistance of the battery is negligible. (Consider all ammeters and voltmeters as non ideal)
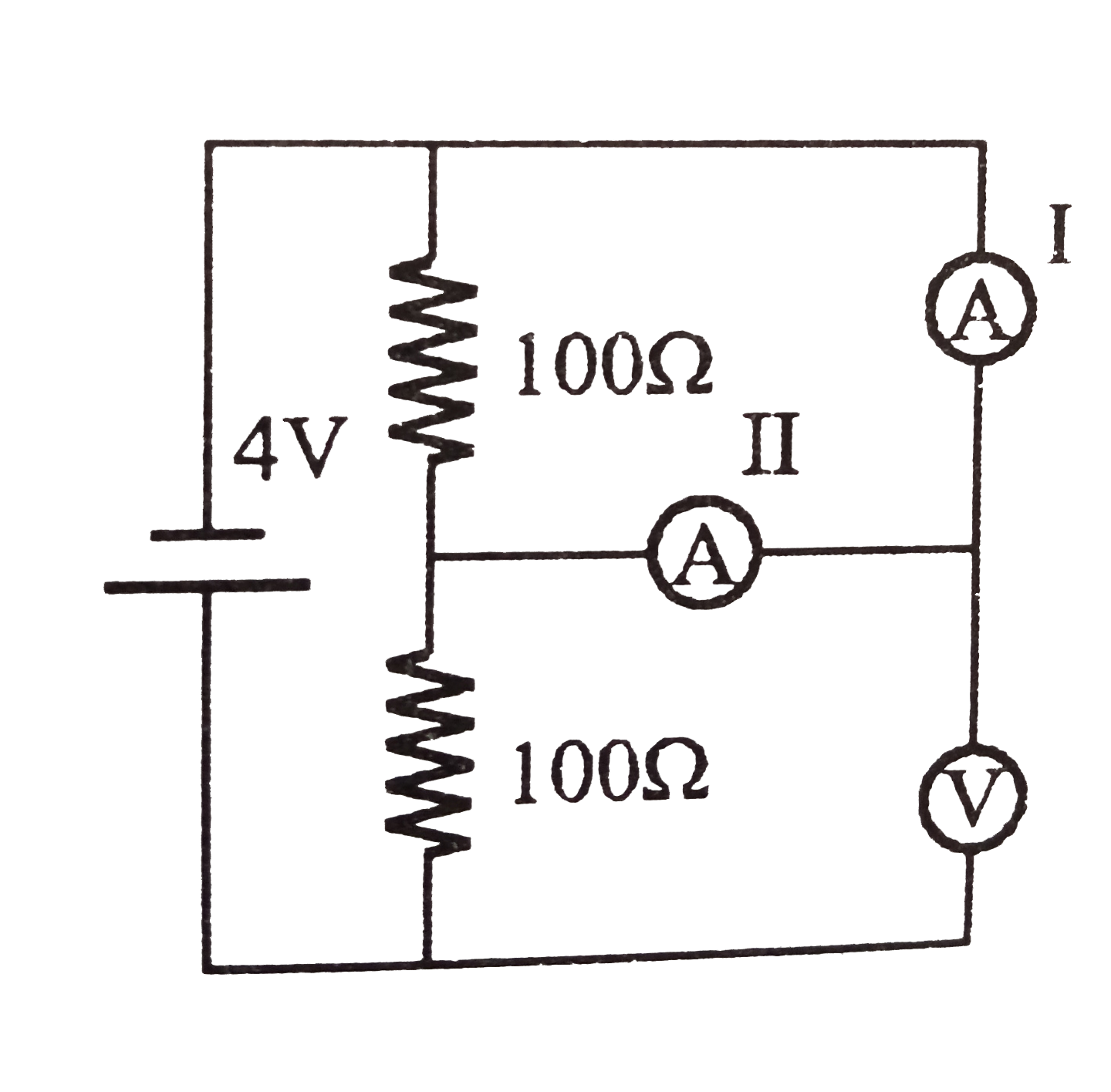 View Solution
View SolutionIn the above question, the reading of ammeter is 200/xmA. What is the value of x?
View SolutionAn ammeter and a voltmeter are connected in series to a battery of emf 6V. When a certain resistance is connected in parallel with the voltmeter, the reading of the latter decreases n = 2 times, whereas the reading of the ammeter increases the same number of times. What is the ratio of the voltmeter resistance to the ammeter resistance? Find the voltmeter reading after the connection.
View SolutionShown an arrangement to measure the emf (ε)and internal resistance r of a battery. The voltmeter has a very high resistance and the ammeter also has some resistance.The voltmeter reads 1.52 V when the switch S is open.When the switch is closed the voltmeter reading drops to 1.45 V and the ammeter read 1.0A Find the emf and the internal resistance of the battery.
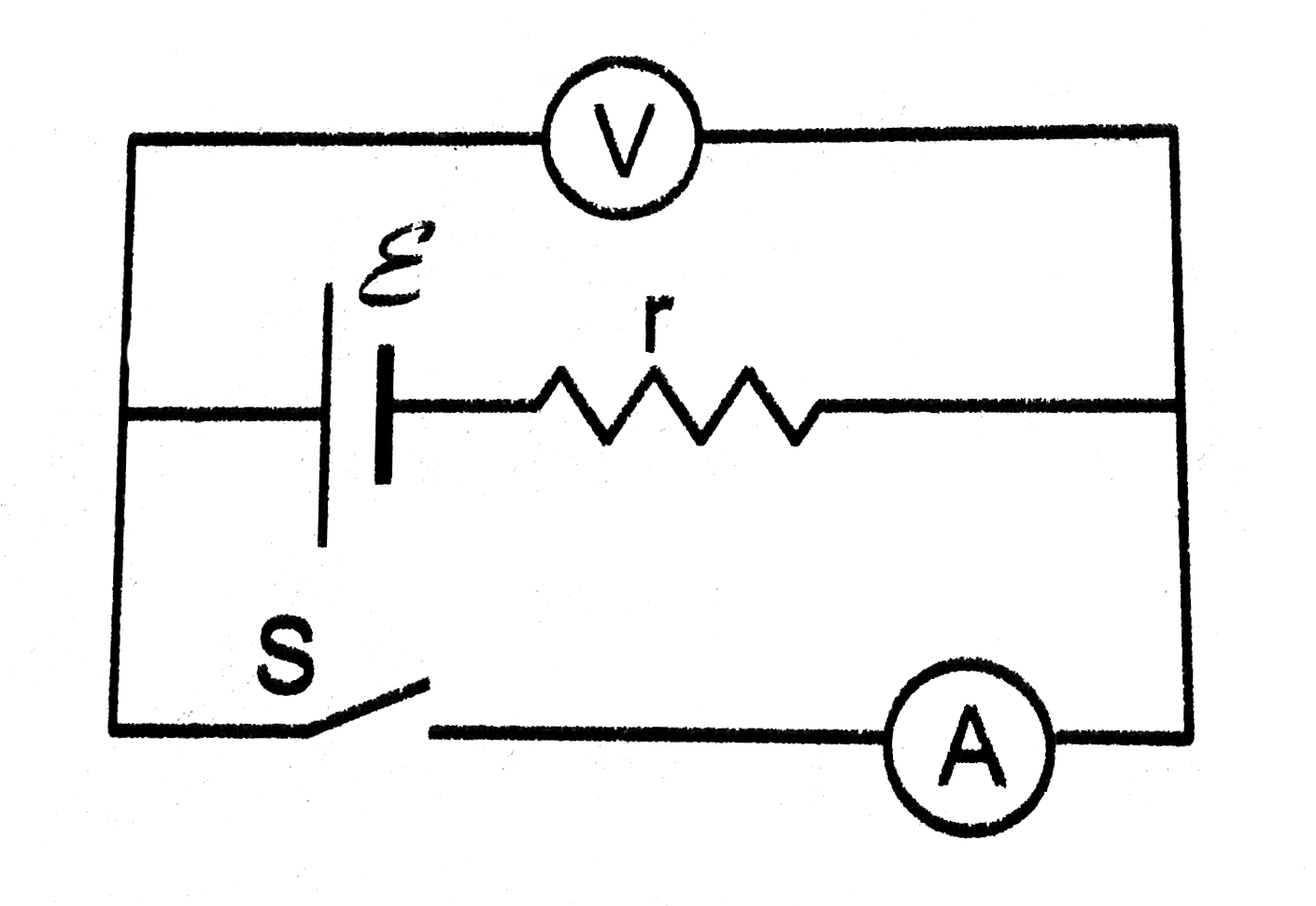 View Solution
View SolutionIn the circuit shown the resistance of voltmeter is 10000ohm and that of ammeter is 20ohm. The ammeter reading is 0.10amp and voltmeter reading is 12 volts. Then R is equal to
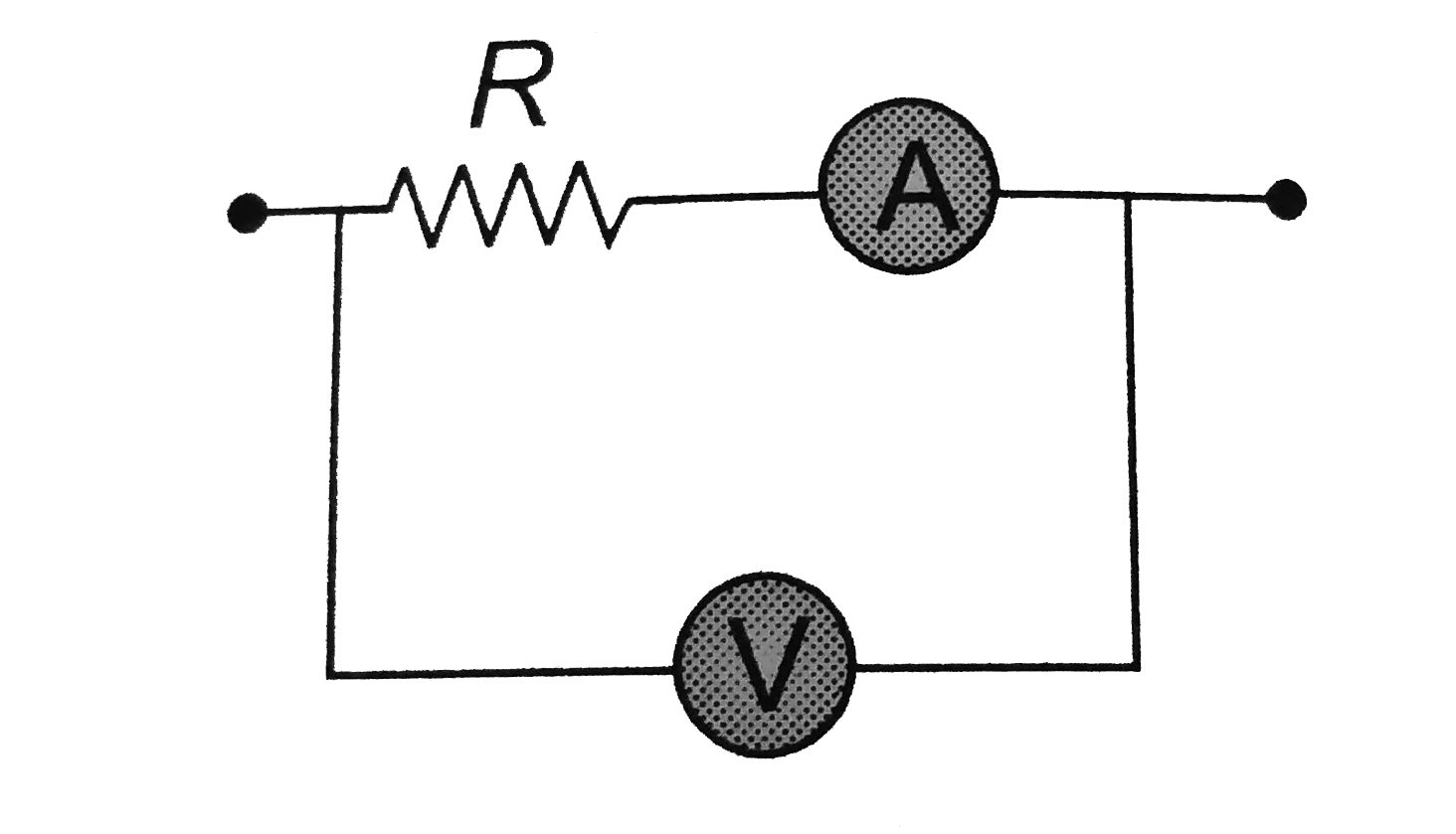 View Solution
View Solution

