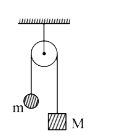
In the arrangement shown in Fig. 7.100 , mass can be hung from a strin

In the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of $2 \times 10^{- 3} k g / m$ that passes over a light pulley . The string is connected to a vibrator of frequency $700 H z$ and the length of the string between the vibrator and the pulley is $1 m$ .

If the standing waves are observed , the largest mass to be hung is
A $16 k g$
B $25 k g$
C $32 k g$
D $400 k g$
In the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of $2 \times 10^{- 3} k g / m$ that passes over a light pulley . The string is connected to a vibrator of frequency $700 H z$ and the length of the string between the vibrator and the pulley is $1 m$ .

The string is set into vibrations and represented by the equation $y = 6 sin (\frac{π x}{10}) c m cos (14 \times 10^{3} π t)$ where $x$ ane $y$ are in $c m$ , and $t$ in $s$ , the maximum displacement at $x = 5 m$ from the vibrator is
A $6 c m$
B $3 c m$
C $5 c m$
D $2 c m$
A string of length 0.5m and linear density $10^{- 4}$ kg/m is stretched under a tension of 100 N. If the frequency of the vibration of the string is 4000 Hz, how many loops are formed on the string?
A1
B4
C2
D6

The correct Answer is:C