In the arrangement shown in figure match the following
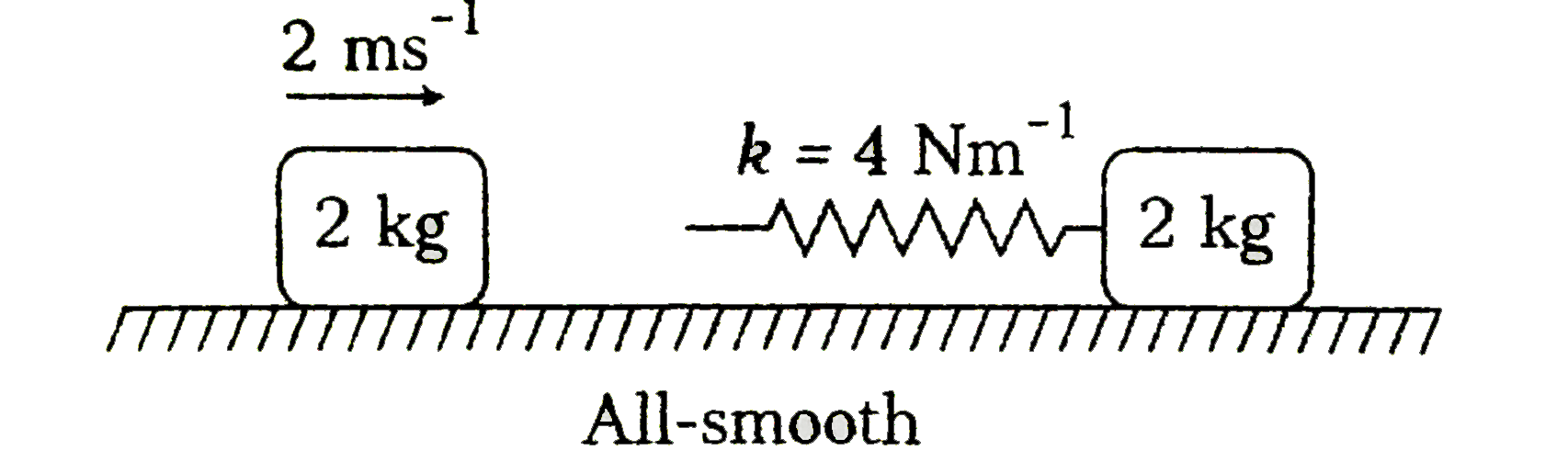
column1column2A Velocities of center of massP 2SI unitB Velocity of combined mass when compression in the spring is maximumQ 1 SI unitC Maximum compression in the springR 4 SIunitD Maximum potential energy stored in the springS 0.5SI unit
The correct Answer is:A →q, B →q, C→q, D →p
vCM=(m1v1+m2v2)=1ms−1
During maximum compression also, velocity of combined mass is ms−1.
Now, Umax=K1−K2
12KX2max=2J
We have, Xmax=1m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
In a two block system in figure match the following.
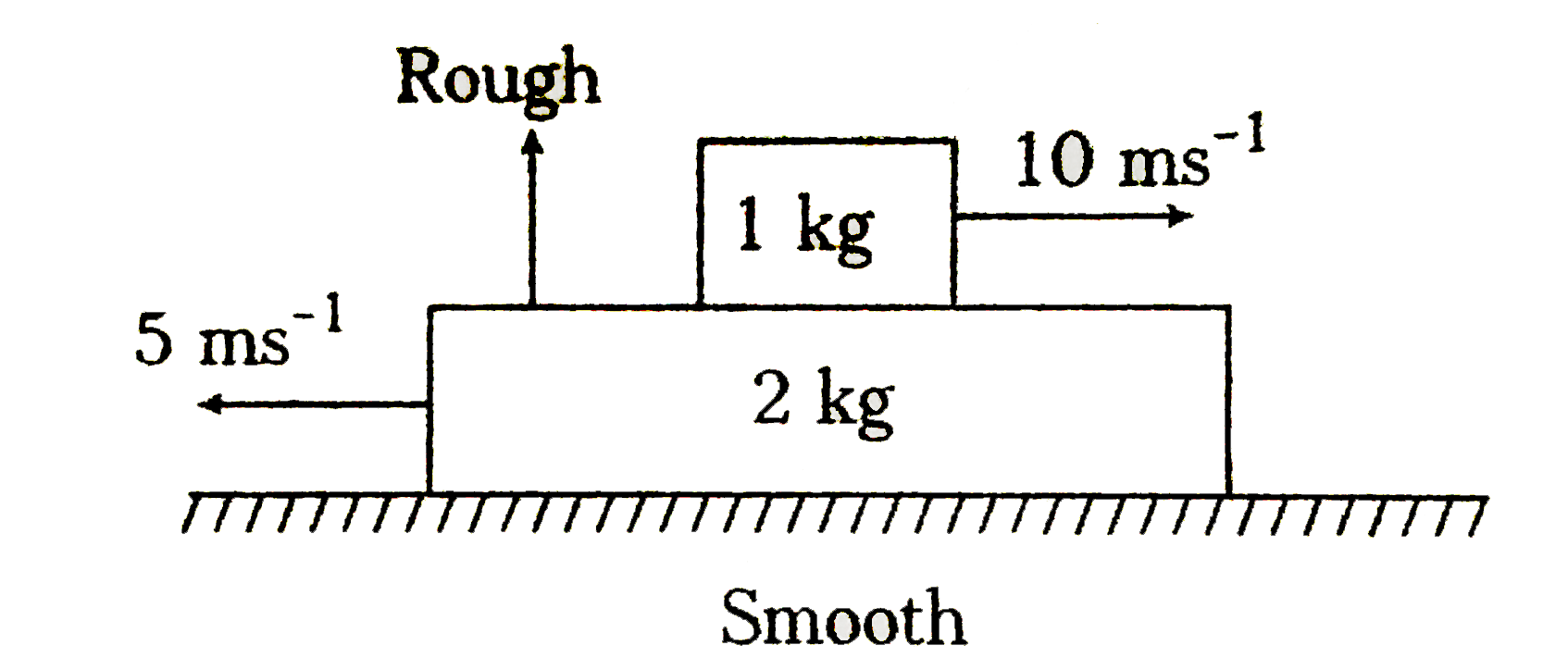 Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
View SolutionIn the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unit
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionIn the diagram shown in figure, match the following (g=10m/s2)

Column-IColoumn-II(A)Acceleration of 2kg block(P)8 Si unit(B)Net force on 3kg block(Q)25 SI unit(C)Normal reaction between 2 kg and 1kg(R)2 SI unit(D)Normal reaction between 3 kg and 2kg (S) 45 SI unit(T) None
View Solution .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
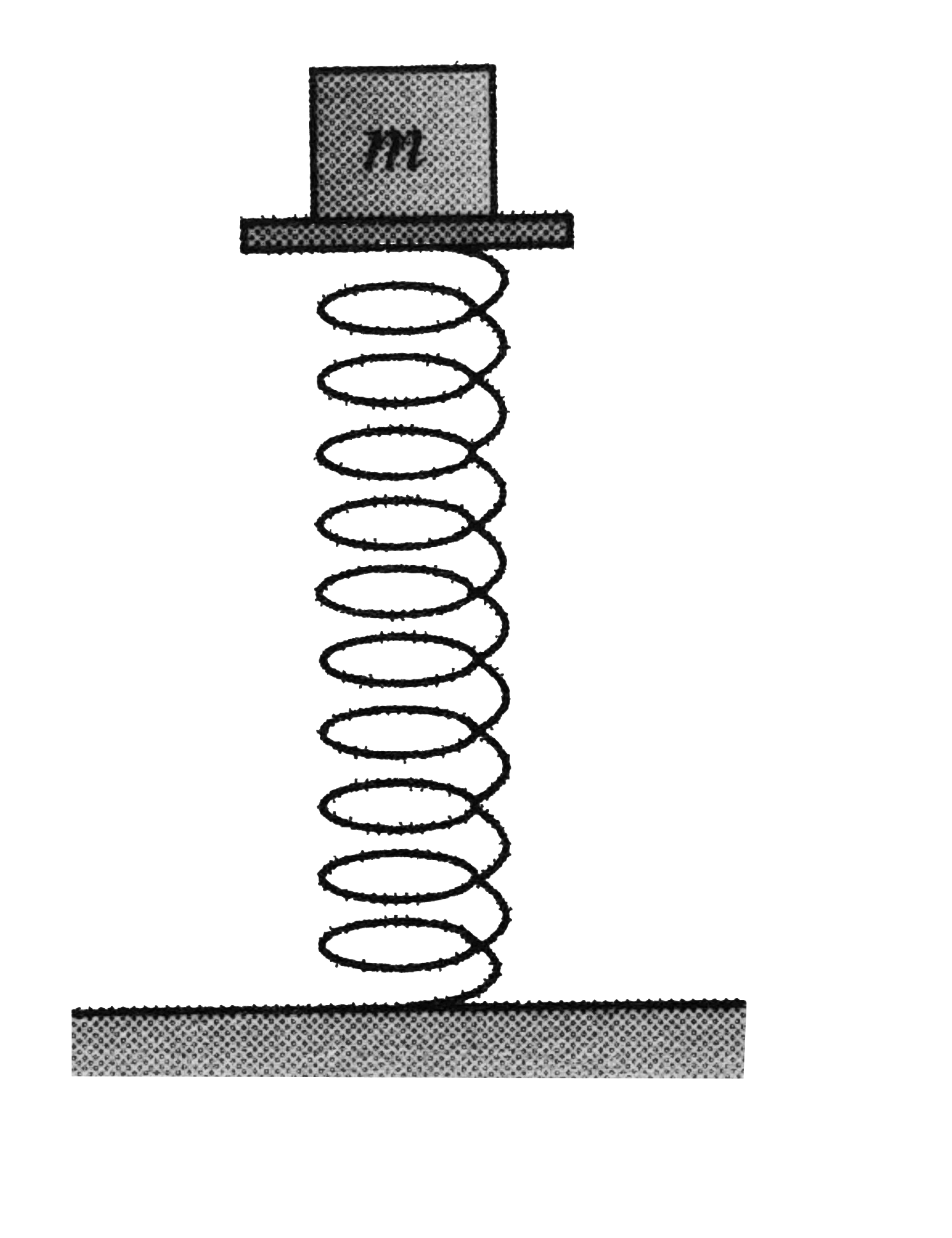
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
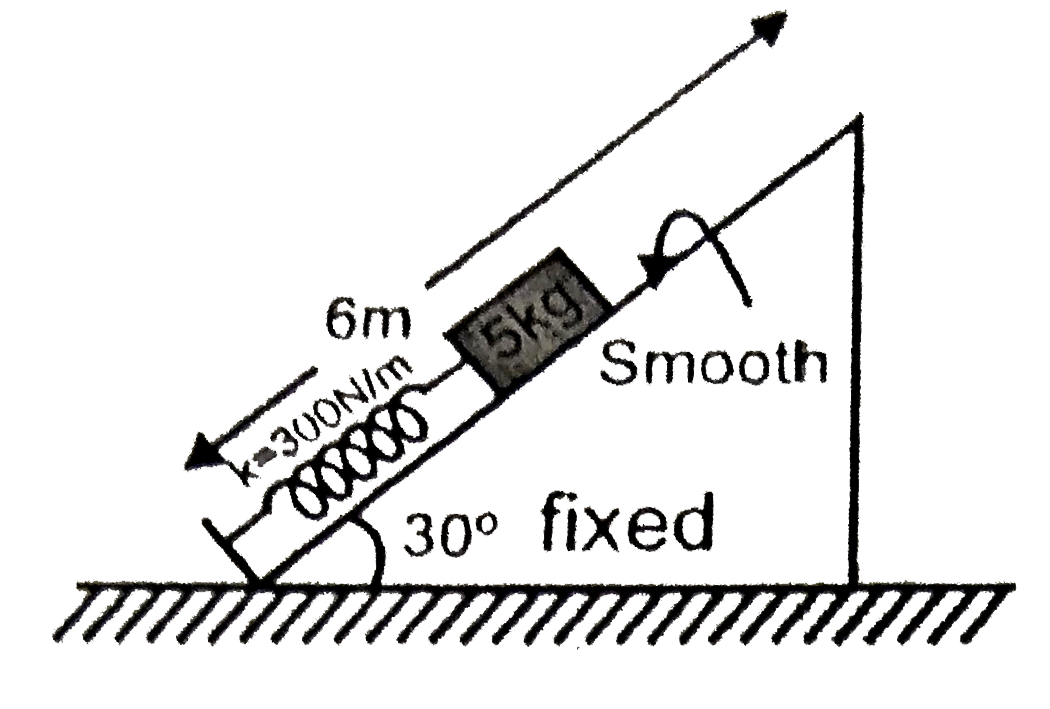
View SolutionA block of mass 5kg is released from rest when compression in spring is 2m. Block is not attached with spring and natural length of the spring in 4m. Maximum height of block from ground is :(g=10m/s2)
View Solution
