In the arrangement shown in figure, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed
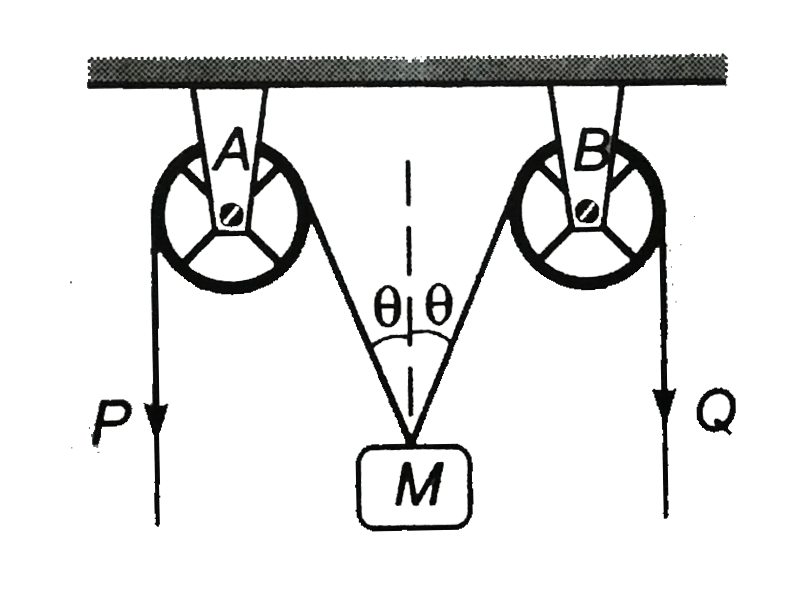
(a) 2Ucosθ (b) Ucosθ (c) 2Ucosθ (d) Ucosθ
Suppose the distance of point Ofrom the ceiling is y and the distance of point Ofrom each pulley is x and the distance between the two pulleys is
x2=y2+124

Differentiating the above equation w.rt to
2x(dxdt)=2y(dydt)+142l(dldt)
But u=−dxdt,v=dydtandusecθ
∴−xu=yvandv=−uxy=usecθ
∴ Velocity of mass =v=usecθ (upward)
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
In the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
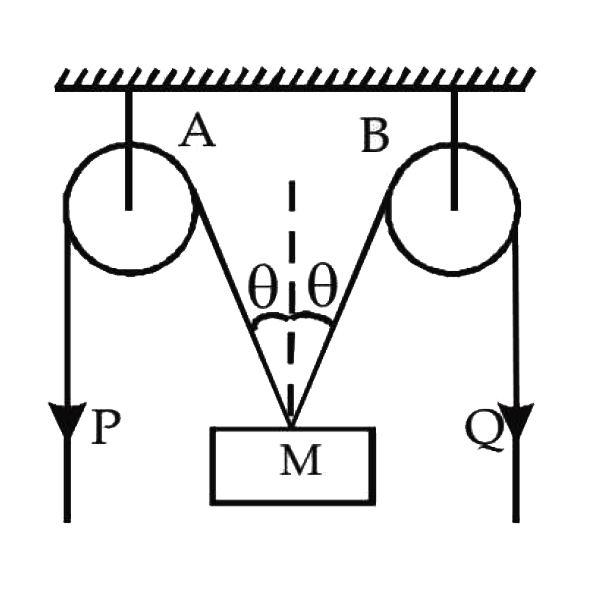
View SolutionIn the arrangement shown in figure, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed

(a) 2Ucosθ (b) Ucosθ (c) 2Ucosθ (d) Ucosθ
View Solution
Knowledge Check
In the arrangement shown in Fig. 15.3.15 the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A nd B are fixed. Mass M moves upwards with a speed.
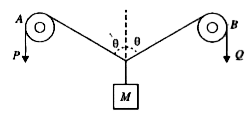 A2 U cosθBU cosθC2 U/cosθDU/cosθ
A2 U cosθBU cosθC2 U/cosθDU/cosθ
In the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed

View Solution∫dθ(sinθ−2cosθ)(2sinθ+cosθ)
View Solution∫d(cosθ)√1−cos2θ
View Solutionlf cos5θ−acos5θ+bcos3θ+ccosθ then c is equal to-
View SolutionThe value of cos4θ+sin4θ−6cos2θ is (a) cos2θ (b) sin2θ (c) cos4θ (d) none of these
View Solutionifacosθ+bsinθ=c. then what is the value of asinθ−bcosθ
View SolutionEvaluate: ∫cos2θln(cosθ+sinθcosθ−sinθ)dθ
View Solution
