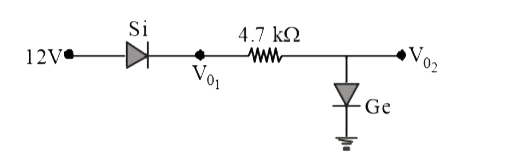In the circuit, shown in fig vs=0.2V,v0=−10V. Find vi and gain Av=v0/vi and A′v=v0vs?

The correct Answer is:NA
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the circuit shown in figure, Voltage V0 is
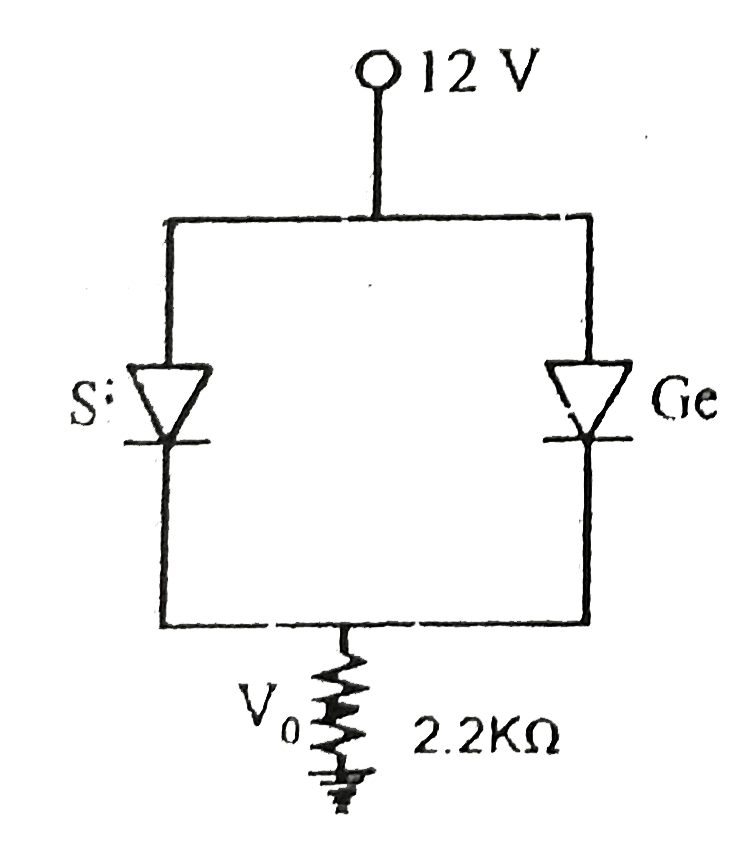 A11.7 voltB11.3 voltC0DNone
A11.7 voltB11.3 voltC0DNone
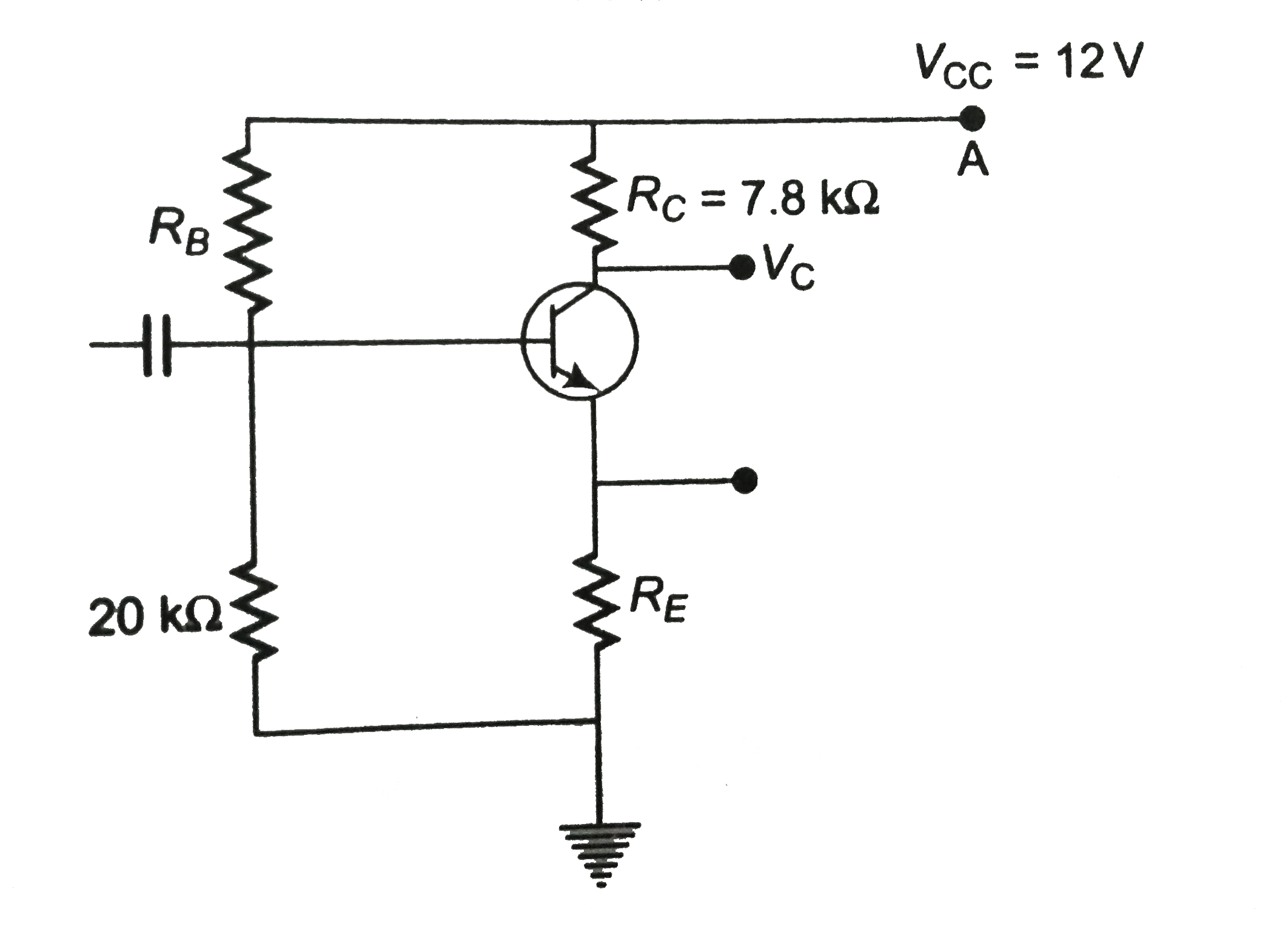
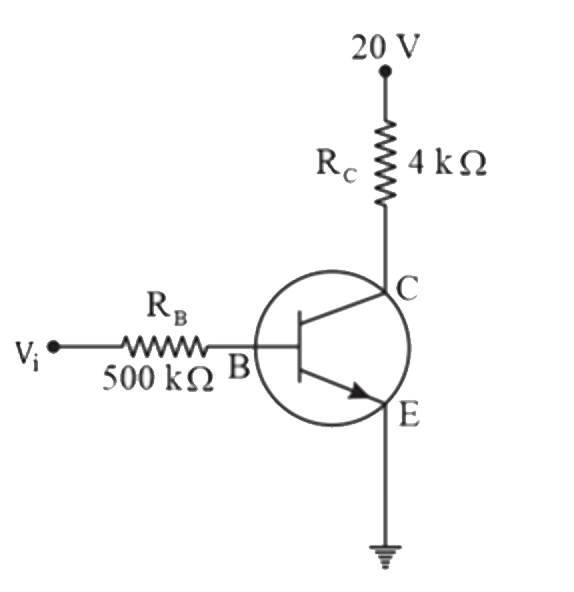
In the circuit shown infigure, voltage V0 is,A11.7 voltB11.3 voltC0DNone of theseIn the circuit shown in the figure, the input voltage Vi is 20V, VBE=0 and VCE=0. The values of IB, IC and β are given by
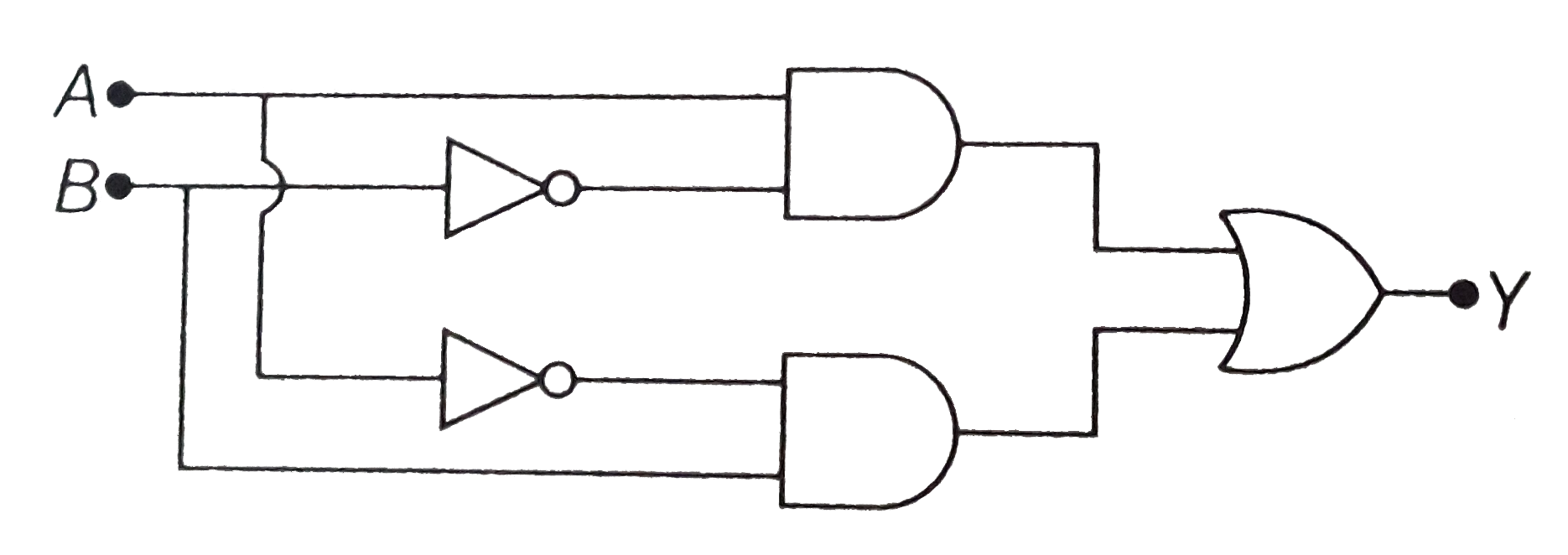 A¯¯¯¯¯¯¯¯A.B+A.BBA.¯¯¯B+¯¯¯A.BC¯¯¯¯¯¯¯¯A.BD¯¯¯¯¯¯¯¯¯¯¯A+B
A¯¯¯¯¯¯¯¯A.B+A.BBA.¯¯¯B+¯¯¯A.BC¯¯¯¯¯¯¯¯A.BD¯¯¯¯¯¯¯¯¯¯¯A+B
Graphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
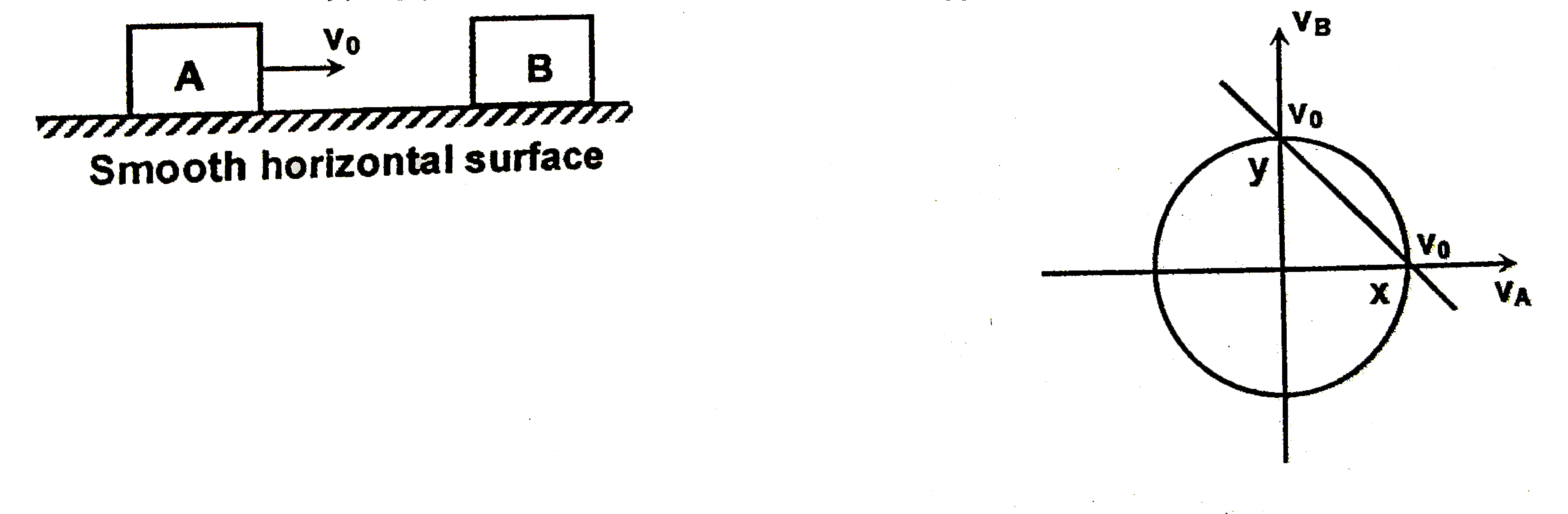
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot is
View SolutionIn the circuit shown in the figure, the input voltage Vi is 20V,VBE=0 and VCE=0. The values of IB,IC and β are given by:
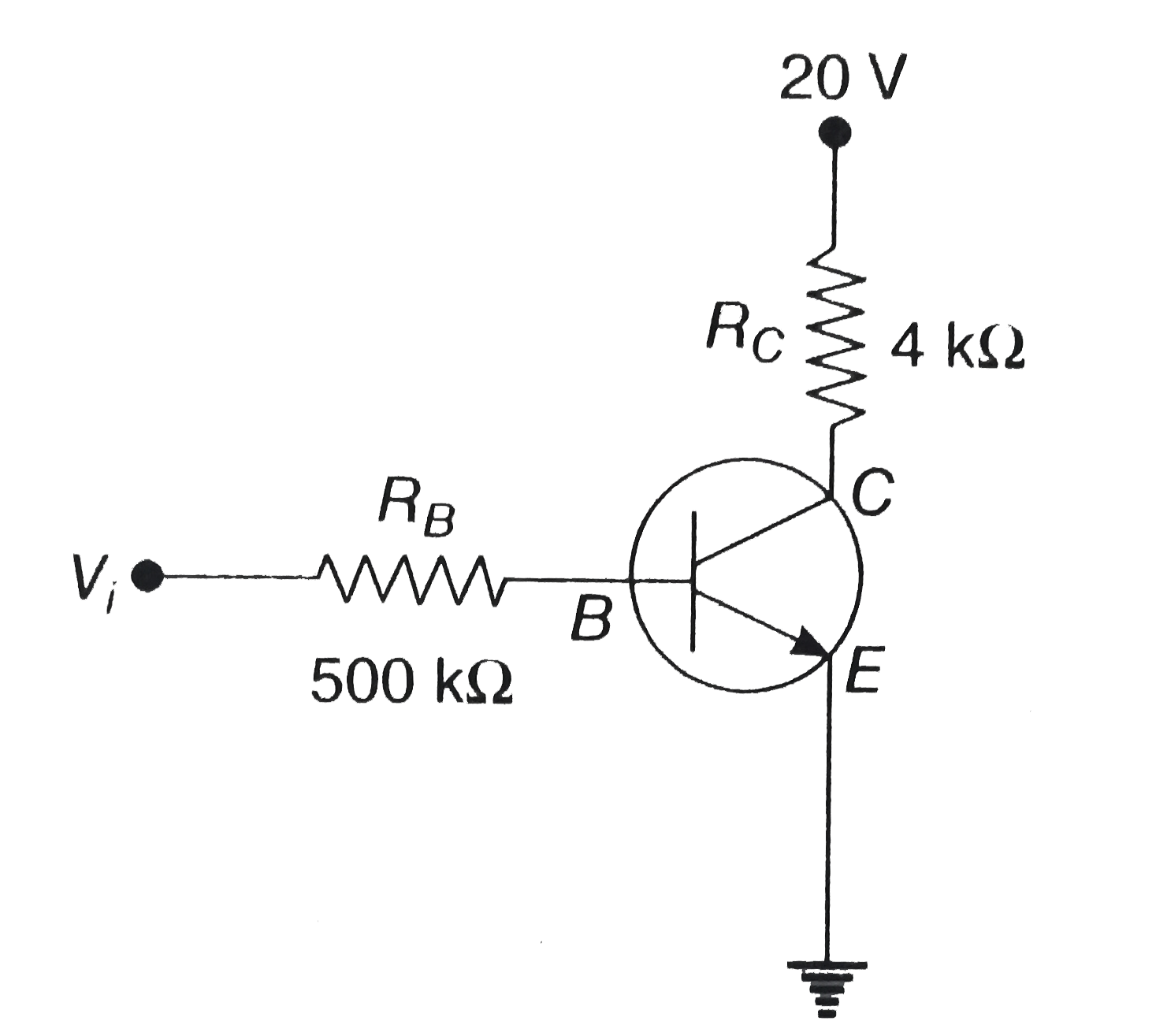
View SolutionIn the circuit shown in the figure, the input voltage Vi is 20V,VBE=0 and VCE=0. The values of IB,IC and β are given by:

View SolutionIn the circuit shows in the figure, the input voltage
Vi is 20 V, VBE=0 and VCE=0. The values of lB,lC and β are given by
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.

So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot is
View Solution