In the circuit shown in figure, initially K1 is closed and K2 is open. What are the charges on each capacitors ? Then K1 was opened and K2 was closed (order is in important), what will be the charge on each capacitor now? (C = 1 μF ]
![In the circuit shown in figure, initially K(1) is closed and K(2) is open. What are the charges on each capacitors ? Then K(1) was opened and K(2) was closed (order is in important), what will be the charge on each capacitor now? (C = 1 muF ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/KPK_AIO_PHY_XII_P1_C02_E03_031_Q01.png) Solution in Gujrati
Solution in Gujrati
When K2 is open and K1 is closed the capacitor C1 and C2 will charge and potential develops across them are V1 and V2 respectively.
E=V1+V2
q=V1+V2
For series connection V=qC ,q is constant
∴V∝1C
∴V1V2=C2C1
∴V1V2=36
∴V2=2V1
From equation (1)
V1+V2=9
V1+2V1=9
3V1=9 V1=3V
and V2=2V1=2×3=6V
Q1=C1V1=6C×3=18μC
and Q2=C2V2=3C×6=18μC [∵C=1μF]
and Q3=0
Now K1 is open and K2 is closed then C2 and C3 connected in parallel and C1 is in series.
∴Q2=Q2+Q3
If V is the common potential of parallel connection
∴V=Q2C1+C2=183C+3C=186C=3V
∴Q2=C2V=3C×3=9μC
[∵C=1μC]
and Q3=C3V=3C×3=9μC
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( Multiple Choice Questions (MCQs) )
93 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )
39 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section C ( NCERT Exemplar Solution ) (Short ,Aswer Type Questions )
5 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
When a unit positive charge moves from one point to another point in an electric field, work done on it ......
View SolutionCapacitance of a capacitor 100 μ F. The work is done for depositing chargc 8×10−18 C on it will be .........
View SolutionProve that a closed equipotential surface with no charge within ilself must enclose an equipotential volume.
View SolutionDetermine the current in each branch of the given network.
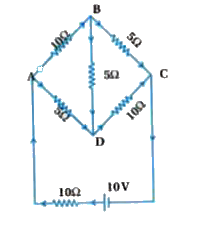
View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionIn the circuit shown in Fig, instially K1 is closed and K2 is open . What are the charges on each capacitor.
Then K1 was opened and K2 was closed (order is important). What will be the charge on each capacitor now ? [C=1μF]
View SolutionIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].
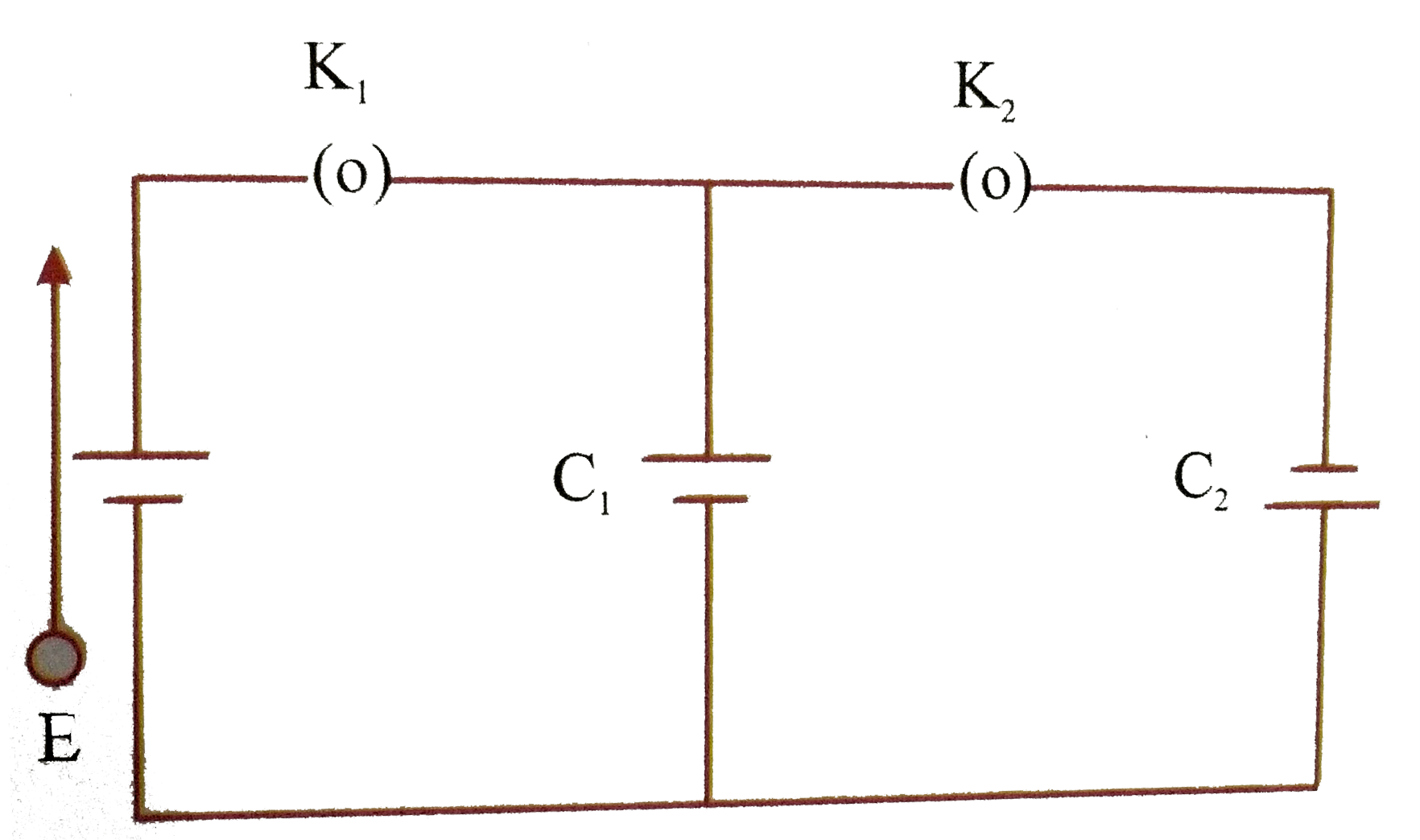
Then
View SolutionIn the given circuit, K_(1) and K_(2) are open initially and the capacotors are uncharged, After K_(1) and K_(2) are closed and steady state is attained. Now answer the following questions. The charge on 4 mu F capacitor is :
View SolutionIn the given circuit, K1 and K2 are open initially and the capacotors are uncharged, After K1 and K2 are closed and steady state is attained. Now answer the following questions.
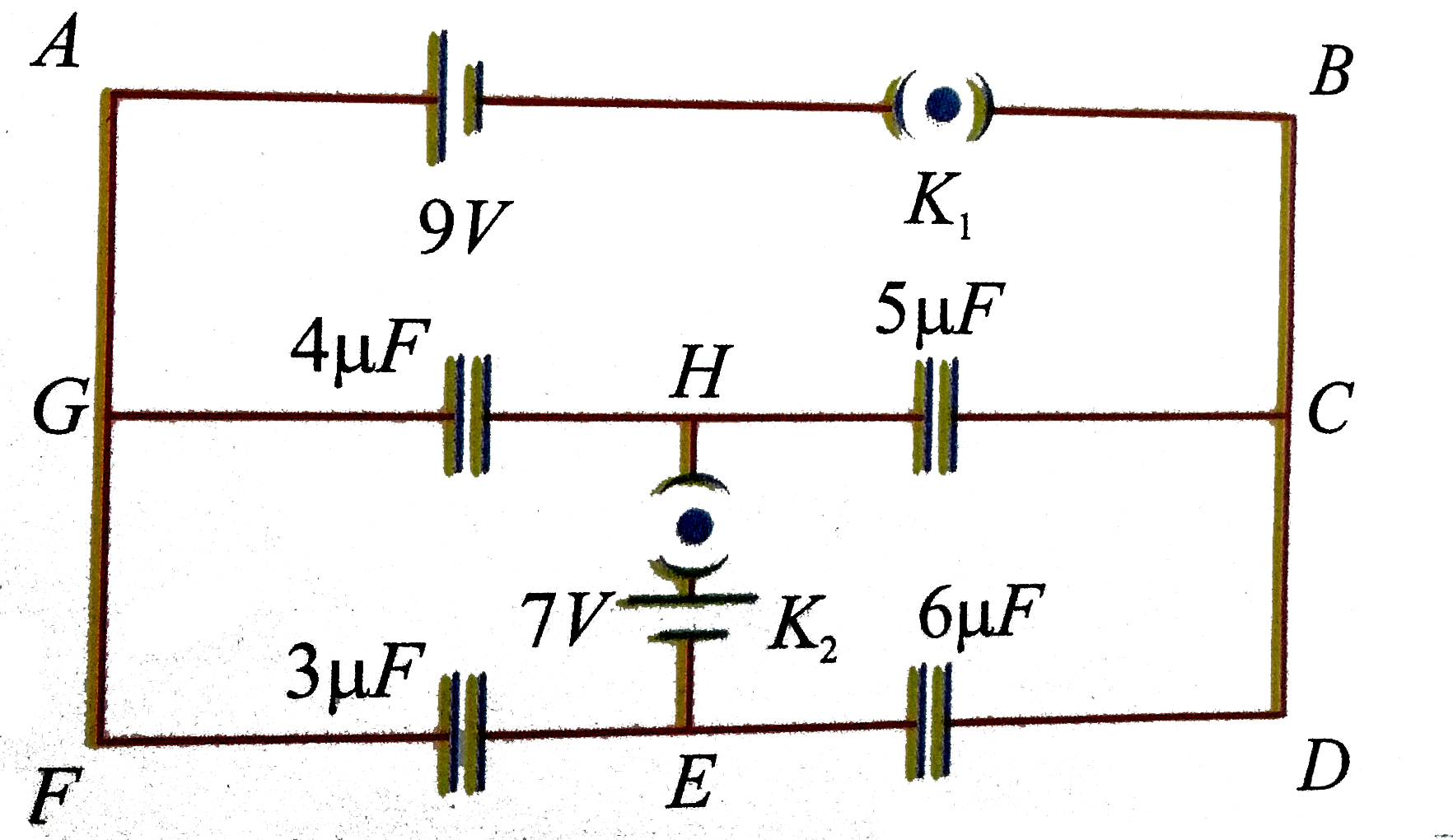
The charge on 5μc capacitor is :
View SolutionIn the given circuit, K_(1) and K_(2) are open initially and the capacotors are uncharged, After K_(1) and K_(2) are closed and steady state is attained. Now answer the following questions. The charge in 3 mu F capacitor is :
View SolutionIn the given circuit, K1 and K2 are open initially and the capacotors are uncharged, After K1 and K2 are closed and steady state is attained. Now answer the following questions.
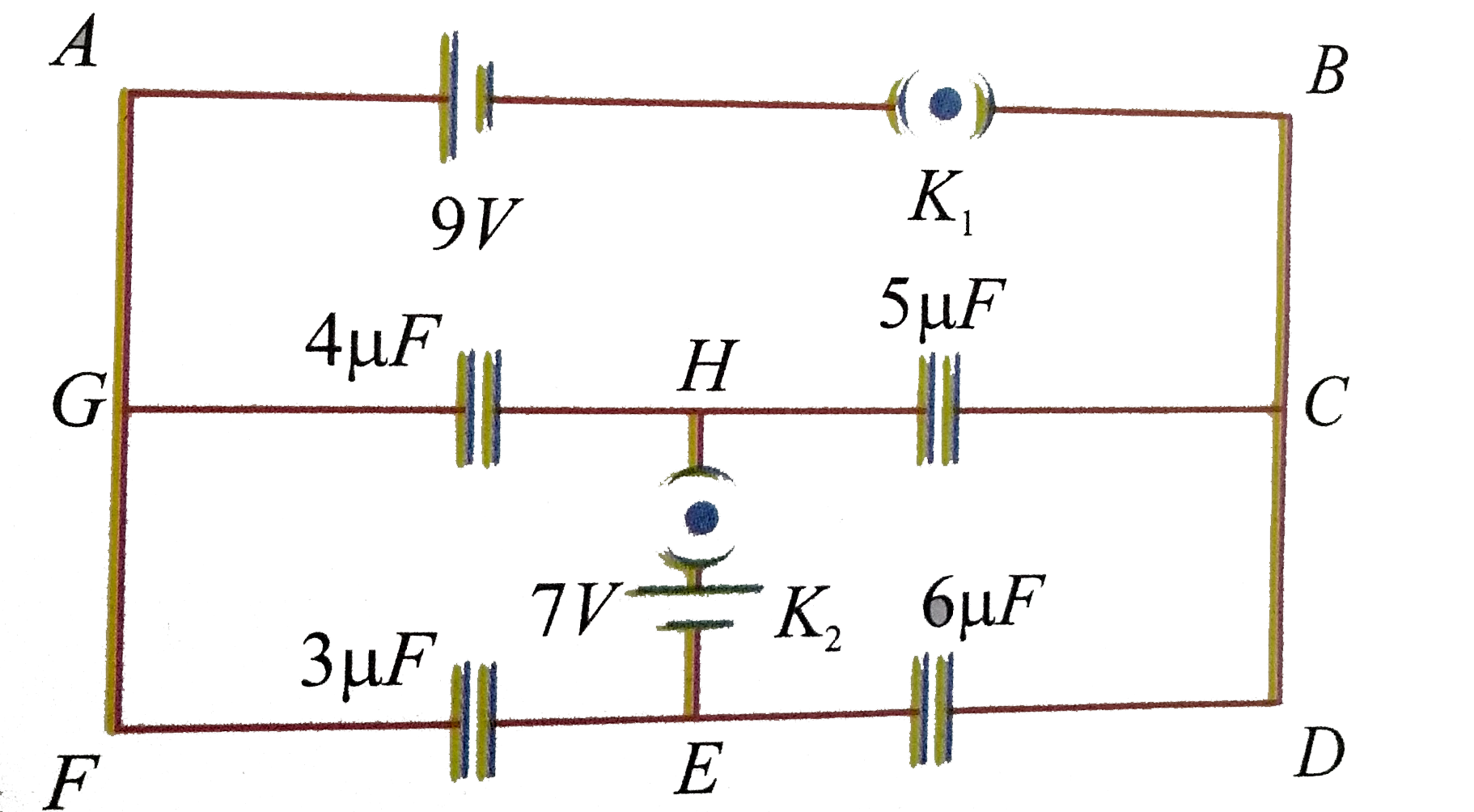
The charge on 6μF capacitor is :
View SolutionShown in the figure is a parallel R , L,C circuit with key K_(1) closed and K_(2) opened . When K_(1) is opened and K_(2) is closed simultaneously find the maximum potential difference across the capacitor and maximum charge stored in it .
View SolutionInitially key in the circuit shown K_(1) Is closed K_(2) Is open. Then K_(1) Is opened and K_(2) Is closed. (Order is important) Q_(1) and Q_(2) Respectively C_(1) and C_(2) Charge and V_(1) and V_(2) Potential, then
View SolutionIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].

Then
View SolutionIn the circuit shown in figure , initially key K_(1) is closed and key K_(2) is open. Then K_(1) is opened and K_(2) is closed (order is important). [Take Q_(1)^(') and Q_(2)^(') as charges on C_(1) and C_(2) and V_(1) and V_(2) as voltage respectively]. Then
View SolutionA circuit containing capacitors C_(1) and C_(2) shown in Fig. is in the steady state with key K_(1) closed. At the instant t = 0, K_(1) is opened and K_(2) is closed. The angular frequency of oscillation of the circuit is
View Solution
