In the circuit shown in Fig, initially K1 is closed and K2 is open . What are the charges on each capacitor.
Then K1 was opened and K2 was closed (order is important). What will be the charge on each capacitor now ? [C=1μF]
The correct Answer is:case I:Q1=18μC,Q2=9μCandQ3=0
"case I:" Q_(2) =9/2 mu C, Q_(3) = 9/2mu C
To solve the problem step by step, we will analyze the circuit in two parts: first when switch K1 is closed and K2 is open, and then when K1 is opened and K2 is closed.
Part 1: K1 Closed and K2 Open
1. Understanding the Circuit Configuration:
- Initially, K1 is closed, allowing current to flow through the circuit, while K2 is open, preventing any current from flowing through that branch.
- We have three capacitors: C1, C2, and C3.
2. Identifying Charges on Capacitors:
- Let the charge on capacitor C1 be Q1, on C2 be Q2, and on C3 be Q3.
- Since K2 is open, capacitor C3 will not have any charge, so we have:
Q3=0
3. Capacitors in Series:
- Capacitors C1 and C2 are in series. In a series configuration, the charge on each capacitor is the same:
Q1=Q2=Q
- Therefore, we can denote the charge on both C1 and C2 as Q.
4. Calculating Equivalent Capacitance:
- The equivalent capacitance (C_eq) for capacitors in series is given by:
1Ceq=1C1+1C2
- If we assume C1 = C2 = 1 µF, then:
Ceq=C1⋅C2C1+C2=1⋅11+1=12μF=0.5μF
5. Finding the Total Charge:
- If the voltage across the series combination is V (let’s assume V = 9V), the total charge Q can be calculated using:
Q=Ceq⋅V=0.5μF⋅9V=4.5μC
- Therefore, we find:
Q1=Q2=4.5μCandQ3=0
Part 2: K1 Opened and K2 Closed
1. Switching the Configuration:
- Now, K1 is opened, and K2 is closed. The charge on C1 will remain the same because it is isolated from the circuit:
Q1′=Q1=4.5μC
2. Redistributing Charge:
- Capacitors C2 and C3 are now in parallel since K2 is closed. The charge on C2 (Q2) will redistribute between C2 and C3.
- Since both capacitors have the same capacitance (1 µF), the charge will split equally:
Q2′=Q3′=Q22=4.5μC2=2.25μC
3. Final Charges:
- The final charges on each capacitor are:
Q1′=4.5μC,Q2′=2.25μC,Q3′=2.25μC
Summary of Charges
- Initially (K1 closed, K2 open):
- Q1=4.5μC
- Q2=4.5μC
- Q3=0
- After switching (K1 open, K2 closed):
- Q1′=4.5μC
- Q2′=2.25μC
- Q3′=2.25μC
- Initially, K1 is closed, allowing current to flow through the circuit, while K2 is open, preventing any current from flowing through that branch.
- We have three capacitors: C1, C2, and C3.
- Let the charge on capacitor C1 be Q1, on C2 be Q2, and on C3 be Q3.
- Since K2 is open, capacitor C3 will not have any charge, so we have:
Q3=0
- Capacitors C1 and C2 are in series. In a series configuration, the charge on each capacitor is the same:
Q1=Q2=Q
- Therefore, we can denote the charge on both C1 and C2 as Q.
- The equivalent capacitance (C_eq) for capacitors in series is given by:
1Ceq=1C1+1C2
- If we assume C1 = C2 = 1 µF, then:
Ceq=C1⋅C2C1+C2=1⋅11+1=12μF=0.5μF
- If the voltage across the series combination is V (let’s assume V = 9V), the total charge Q can be calculated using:
Q=Ceq⋅V=0.5μF⋅9V=4.5μC
- Therefore, we find:
Q1=Q2=4.5μCandQ3=0
- Now, K1 is opened, and K2 is closed. The charge on C1 will remain the same because it is isolated from the circuit:
Q1′=Q1=4.5μC
- Capacitors C2 and C3 are now in parallel since K2 is closed. The charge on C2 (Q2) will redistribute between C2 and C3.
- Since both capacitors have the same capacitance (1 µF), the charge will split equally:
Q2′=Q3′=Q22=4.5μC2=2.25μC
- The final charges on each capacitor are:
Q1′=4.5μC,Q2′=2.25μC,Q3′=2.25μC
- Initially (K1 closed, K2 open):
- Q1=4.5μC
- Q2=4.5μC
- Q3=0
- Q1′=4.5μC
- Q2′=2.25μC
- Q3′=2.25μC
Similar Questions
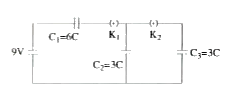
In the ciruit shown in figure, Initially K1 is closed and K2 is open, let charge on capacitor C2 is Q2 Then K1 was opened while K2 kept closed, let charge on capacitor C2 is Q2 (Take, C=1μF ) Then ratio Q2Q1 is
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
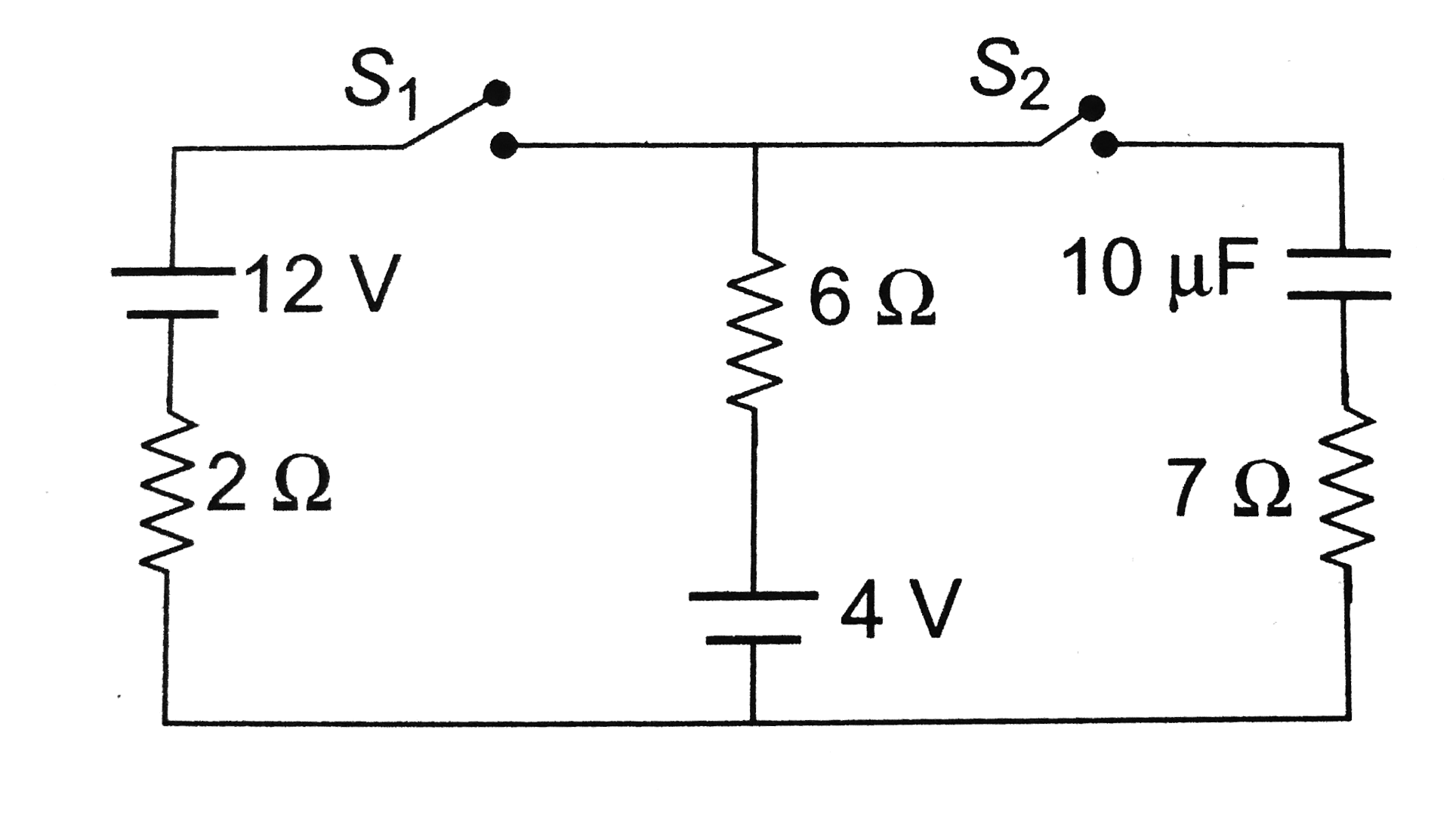
View SolutionIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].
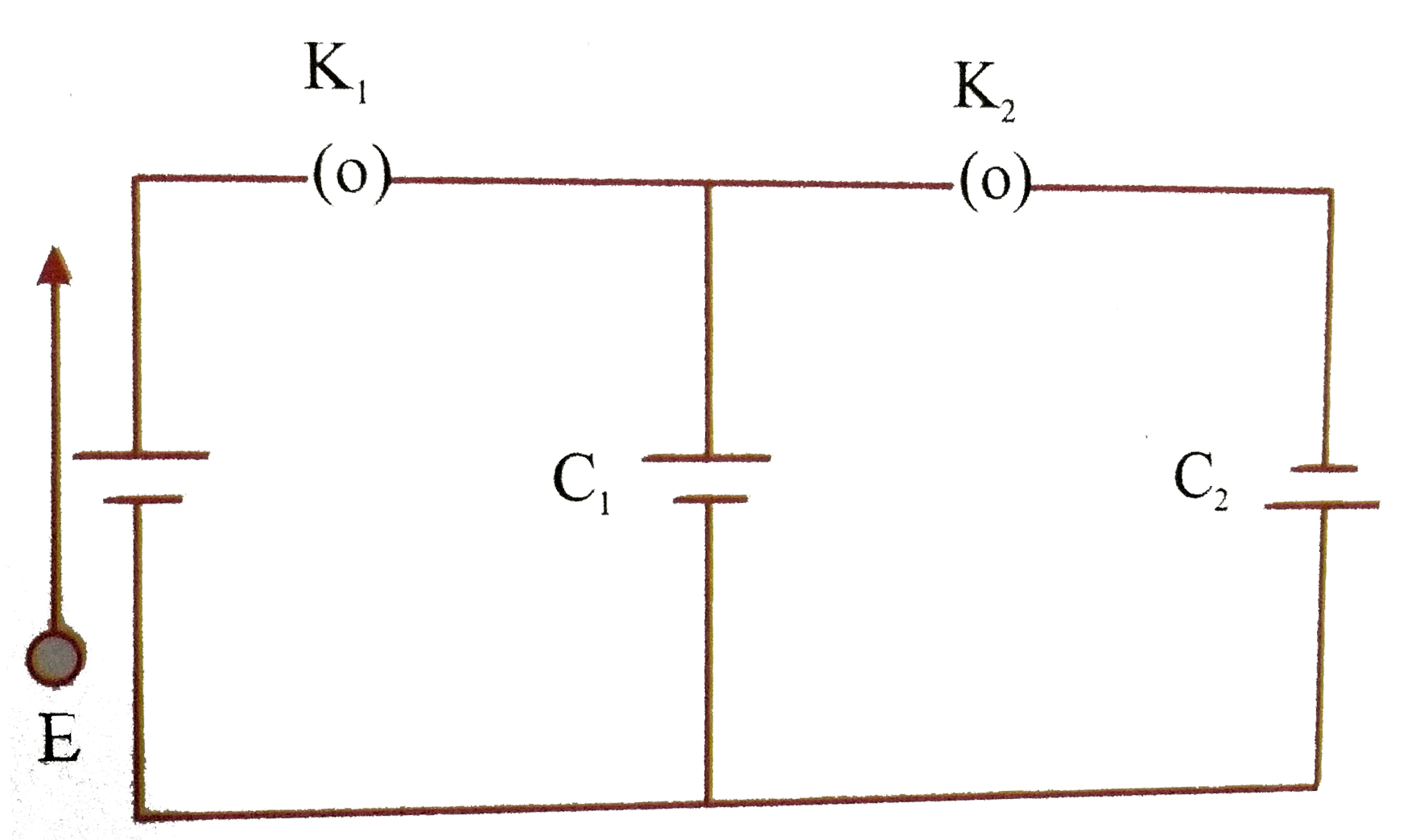
Then
View SolutionIn the circuit shown in figure , initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed (order is important). [Take Q′1 and Q′2 as charges on C1 and C2 and V1 and V2 as voltage respectively].

Then
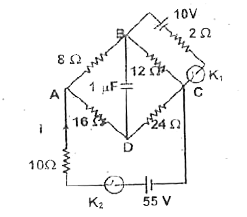
View SolutionConsider the circuit shown in the figure.
(a) Find the current i flowing through the circuit when the keyK1is open and K2 is closed.
(b) Find the net charge on the capacitor when K1 is open & K2 is.closed and also when K1&K2 both are closed.
(c) What is the change in the current'i, when K1 is closed
View SolutionIn the circuit shown in figure initially the switch is opened. The switch is closed now.
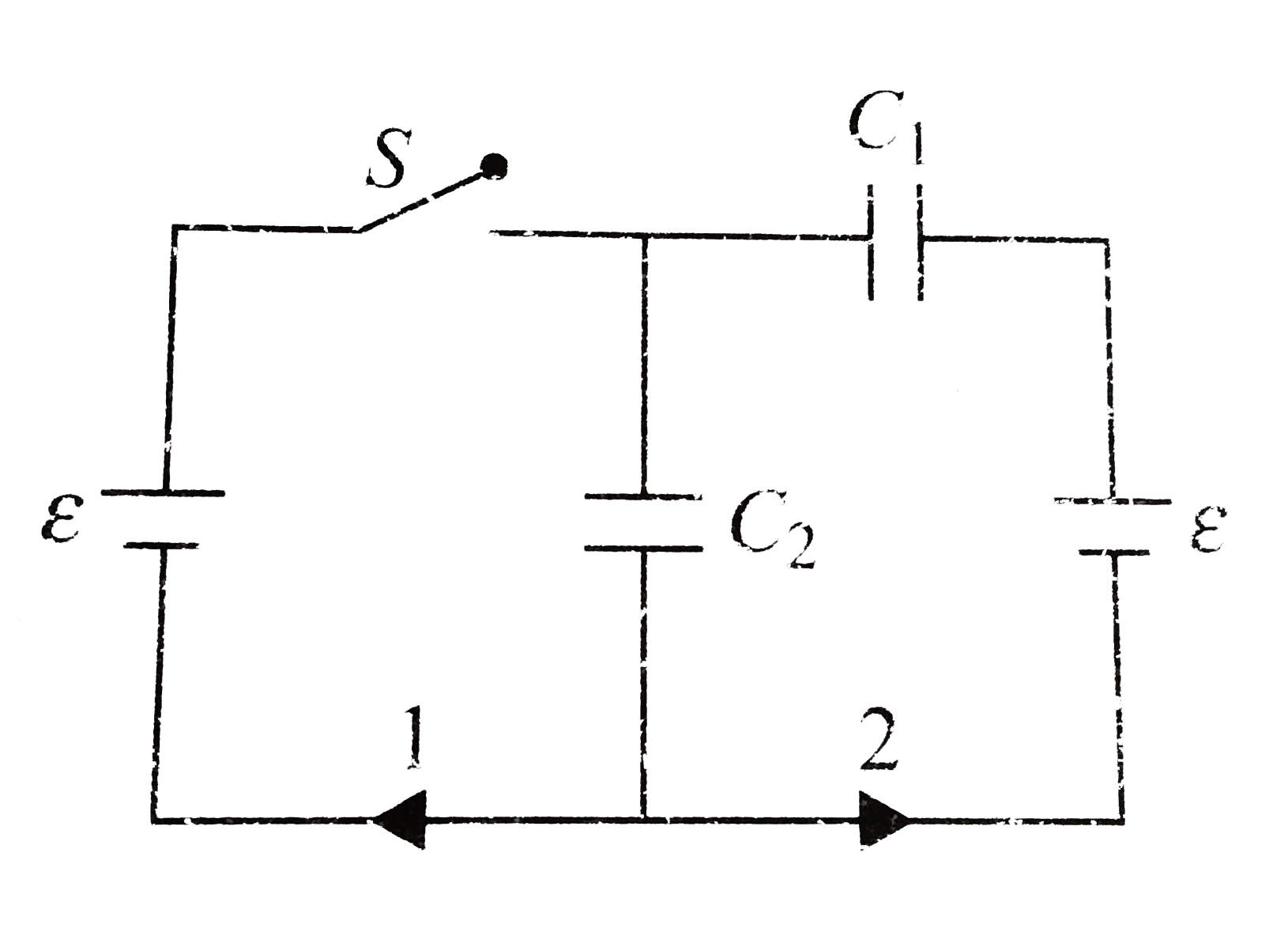
The charge that will flow in direction 1 is
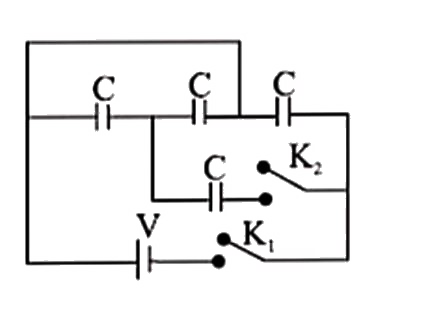
View SolutionInitially K1 is closed, now if K2 is also closed, find heat dissipated in the resistances of connecting wires
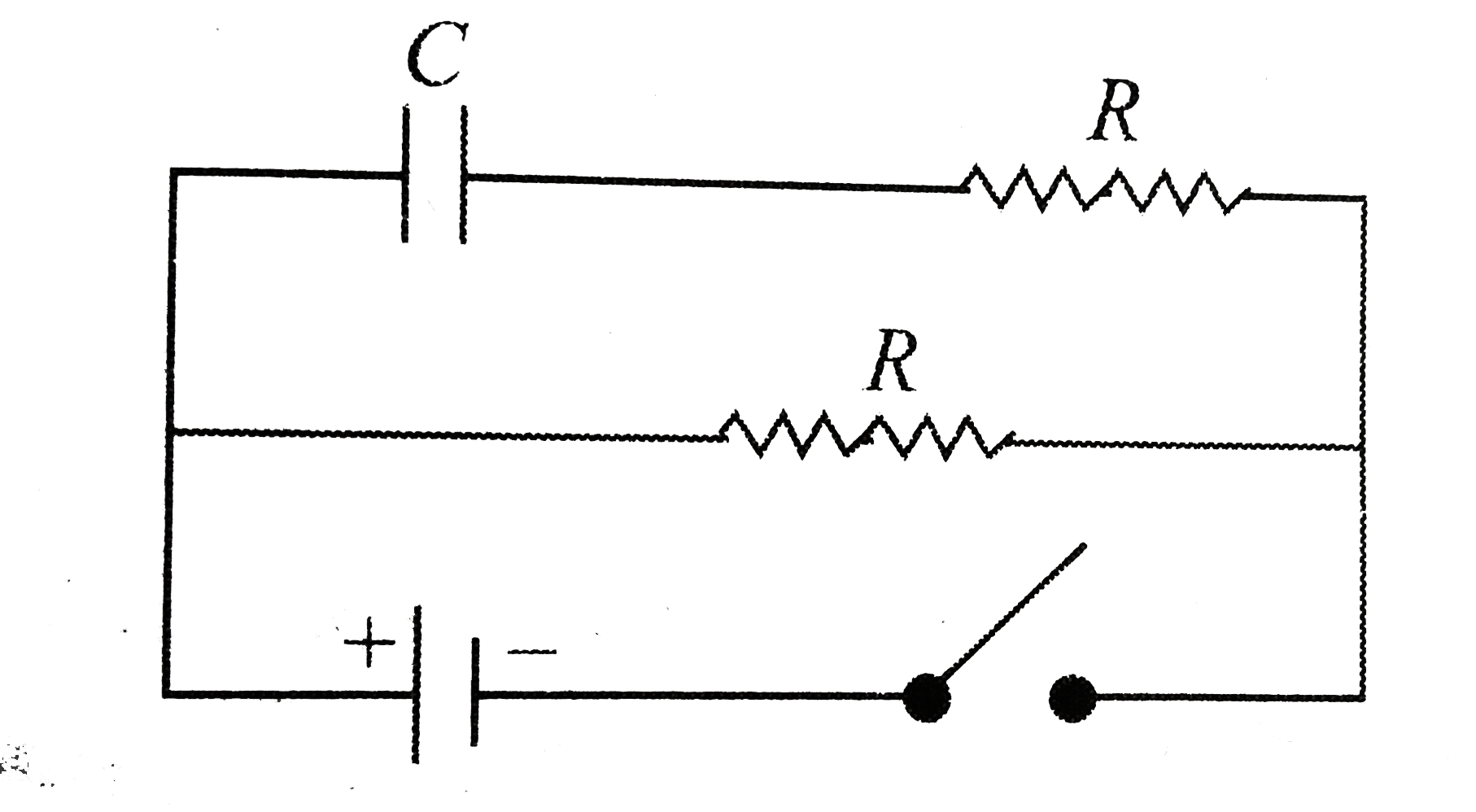
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
View SolutionIn the circuit shown in figure initially the switch is opened. The switch is closed now.

The charge that will flow in direction 2 is
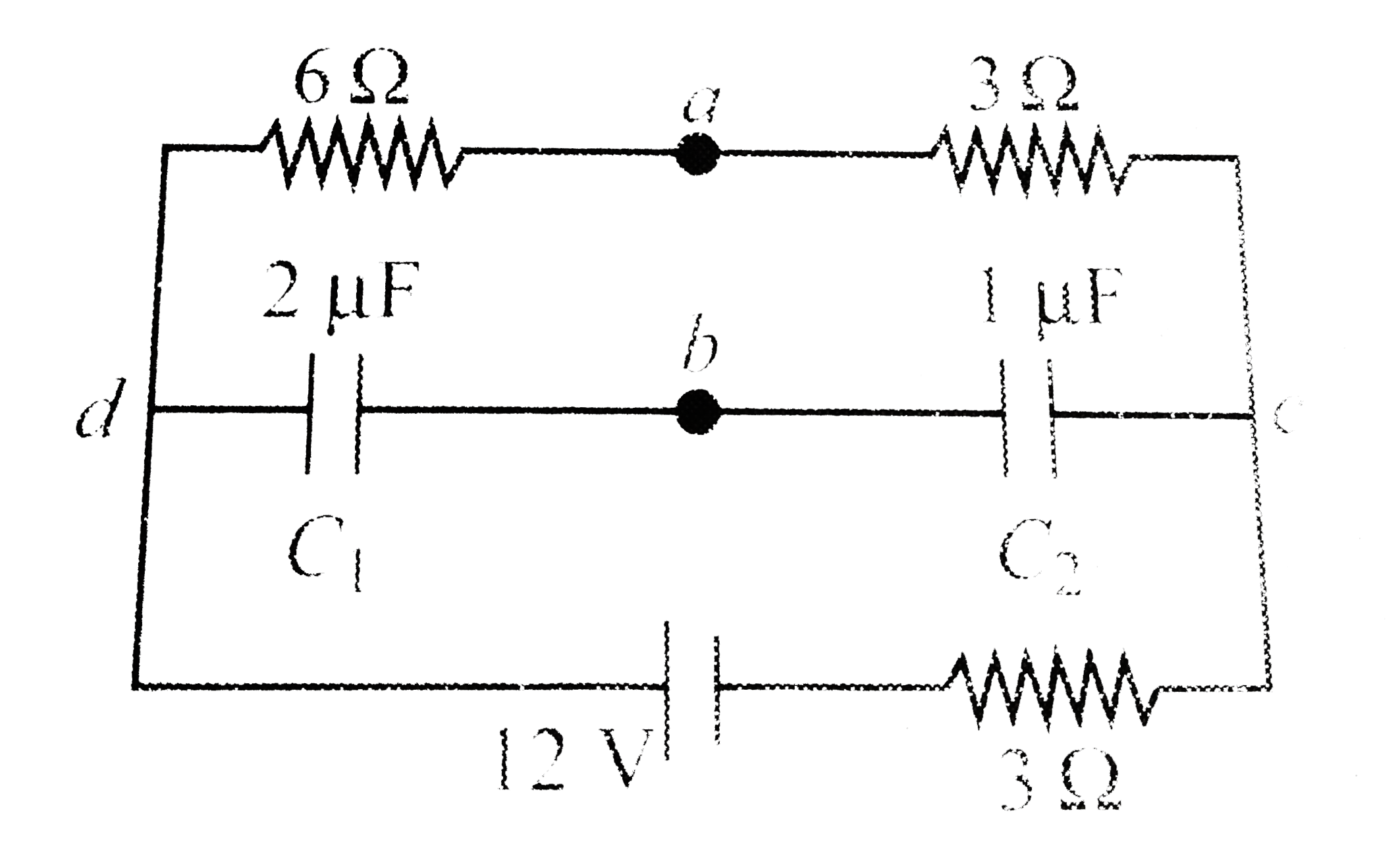
View Solutionwhat is the charge stored on each capacitor C1andC2 in the circuit shown in fig.
View Solution
