In the fig shown, a block of mass M is attached to the spring and another block of mass 2M has been placed over it. The system is in equilibrium. The block are pushed down so that the spring compresses further by . System is released
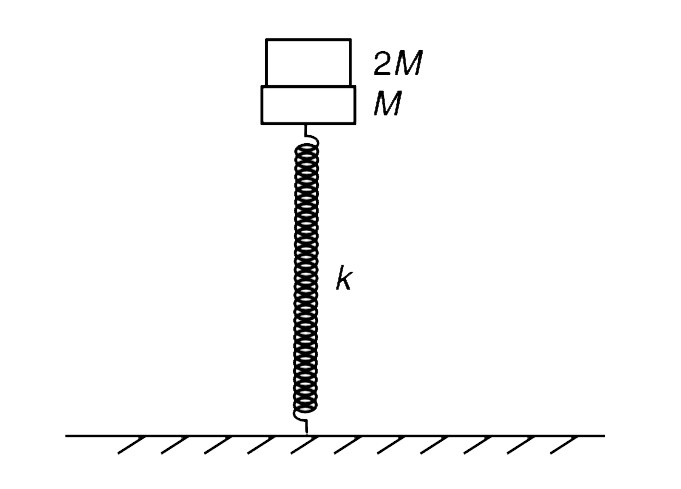
(a) At what height above the position of release, the block of mass 2M will lose contact with the other block? (b) What is maximum height attained by 2M above the point of release?
The correct Answer is:(a)
(b)
Topper's Solved these Questions
Similar Questions
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate.

View SolutionThe block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?

View Solution
Knowledge Check
A bob of mass 2m hanges by a string attached to the block of mass m of a spring blocks syetem. The whole arrangement is in a state of equilibrium. The bob of mass 2m is pulled down slowely by a distance x0 and released.
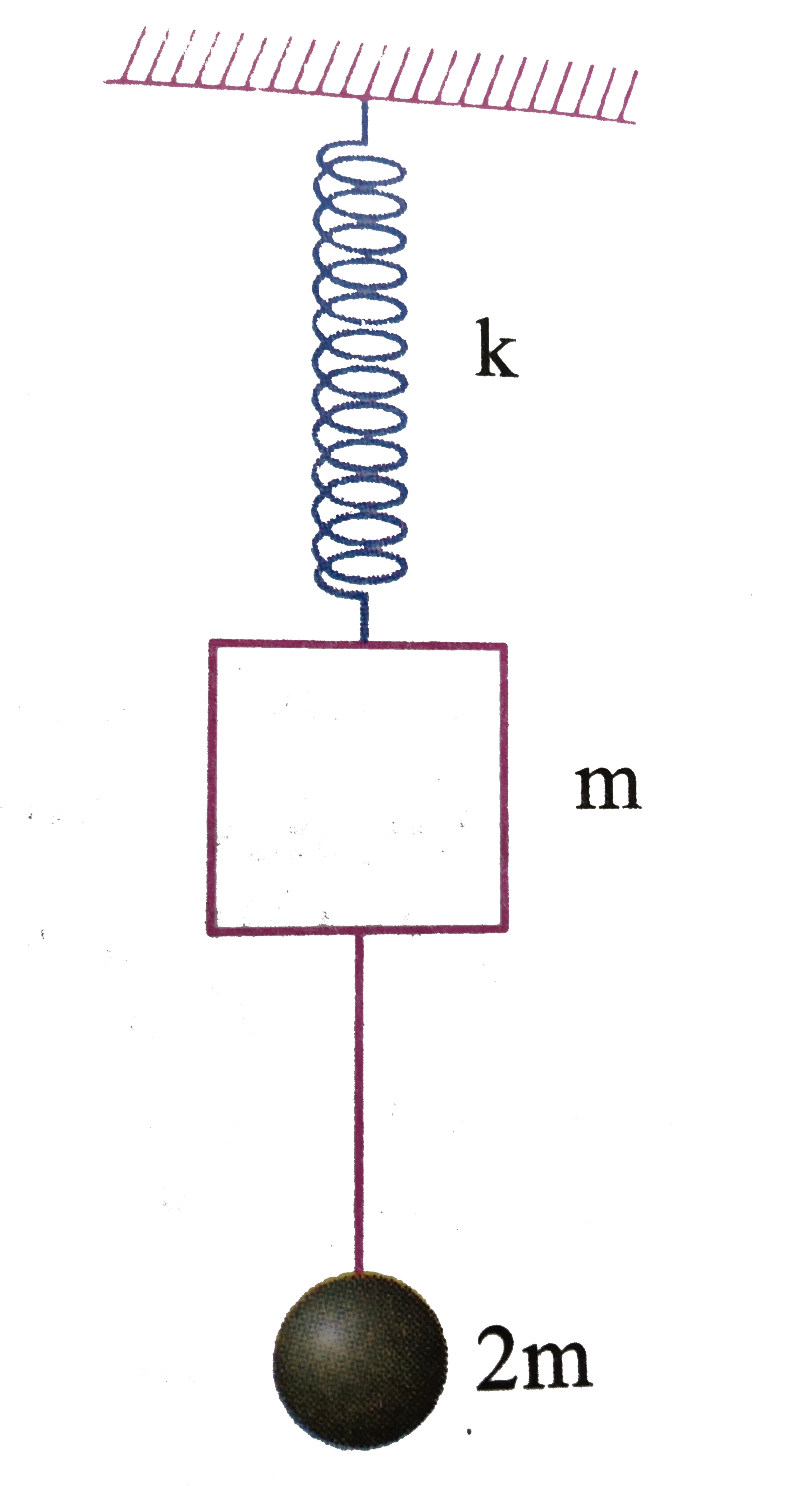 AFor x0=3mgk, maximum tension in string is 4mgBFor x0>3mgk, minimum tension in string is mgCFrequency of oscillation of system is 12π√k3m, for all non-zero values of x0DThe motion will remain simple harmonic for x0≥3mgk
AFor x0=3mgk, maximum tension in string is 4mgBFor x0>3mgk, minimum tension in string is mgCFrequency of oscillation of system is 12π√k3m, for all non-zero values of x0DThe motion will remain simple harmonic for x0≥3mgkIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
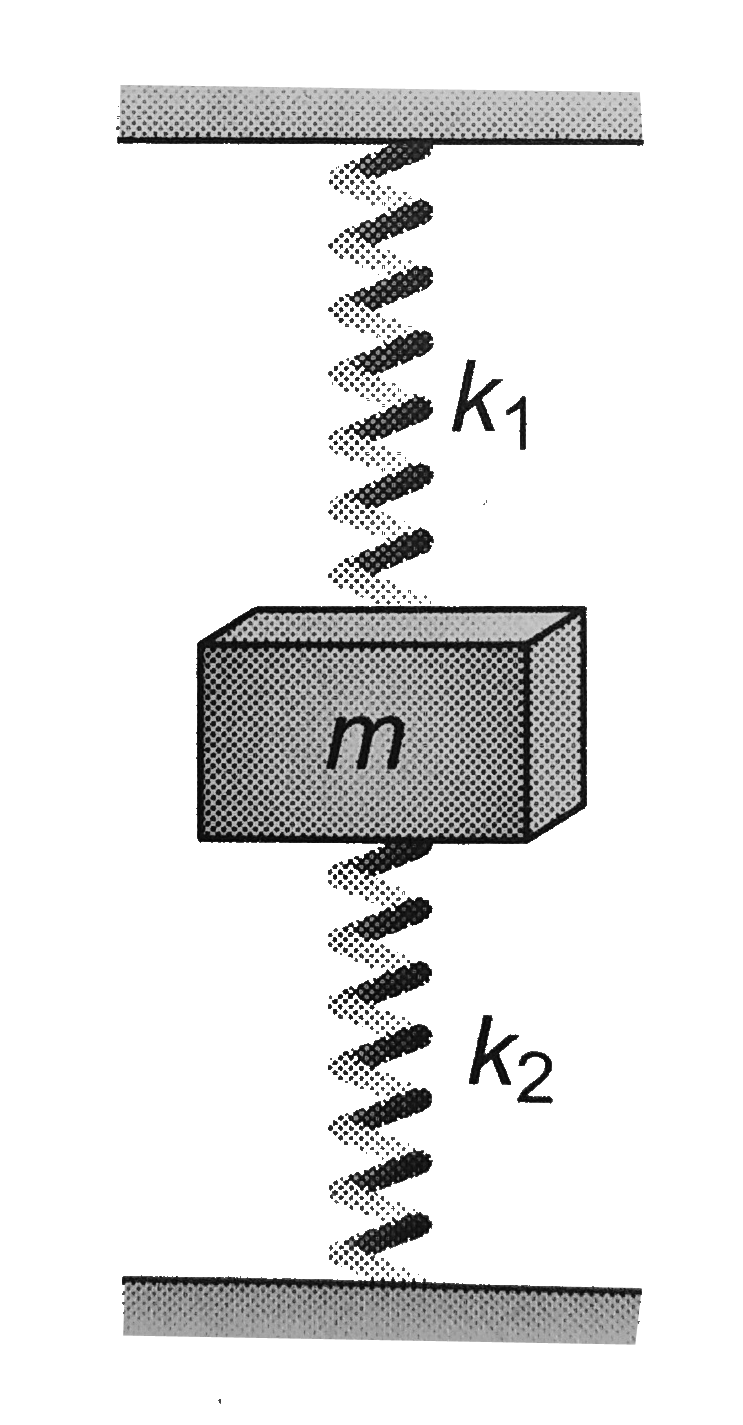 Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
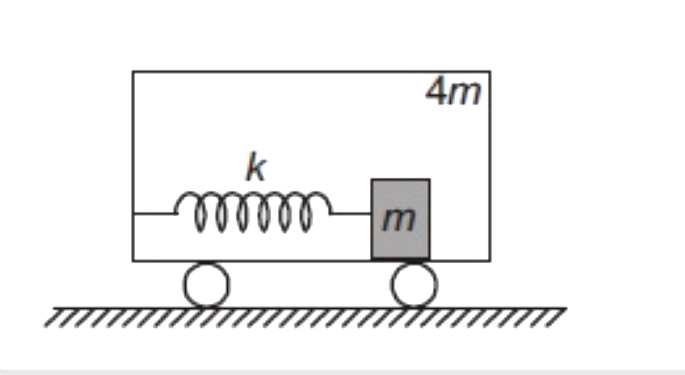
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :

View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View Solution
