A physics student writes the elastic potential energy stored in a spring as U=12KL2+12Kx2, where L is the natural length of the spring, x is extension or compression in it and K is its force constant. A block of mass M travelling with speed V hits the spring and compresses it.
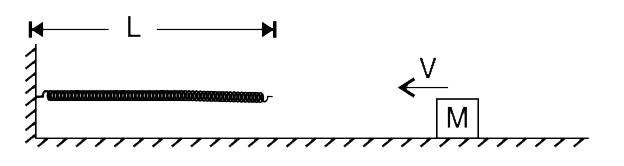
Find the maximum compression caused.
The correct Answer is:√MK.V
Step by step video, text & image solution for A physics student writes the elastic potential energy stored in a spring as U=1/2KL^(2)+1/2Kx^(2), where L is the natural length of the spring, x is extension or compression in it and K is its force constant. A block of mass M travelling with speed V hits the spring and compresses it. Find the maximum compression caused. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
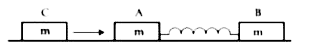 View Solution
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0 - Question 2 - Select One

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2 - Question 3 - Select One
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2k
The ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)
 View Solution
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
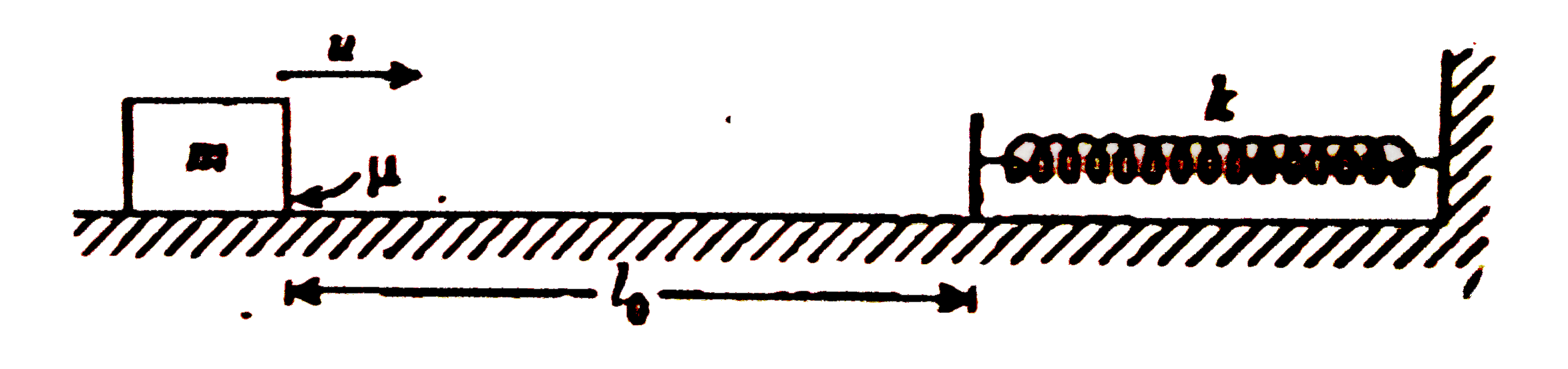 View Solution
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 View Solution
View Solution

