In the figure ABC is the cross-section of a right angled prism and BCDE is the cross-section of a glass slab. The value of theta so that light incident normally on the face AB does not cross the face BC is (Givensin−13/5=37∘)

θ<37∘
θ<53∘
θ≥37∘
θ≥53∘
The correct Answer is:A
sinθC=μRμD=6/53/2=45
r1=0∘⇒r2=<B=90∘−θ
Now, r2>θc
or sinr2>sinθC
∴Sin(90∘−θ)>45
or cosθ>45…(i)
cos37∘=45
From Eq. (i), we see that
θ<37∘
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option3videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions8videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
Calculate the value of θ, for which light incident normally on face AB grazes along the face BC.
μglass=3/2andμwater=4/3
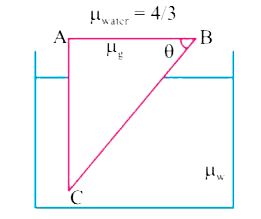 View Solution
View SolutionWhat is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
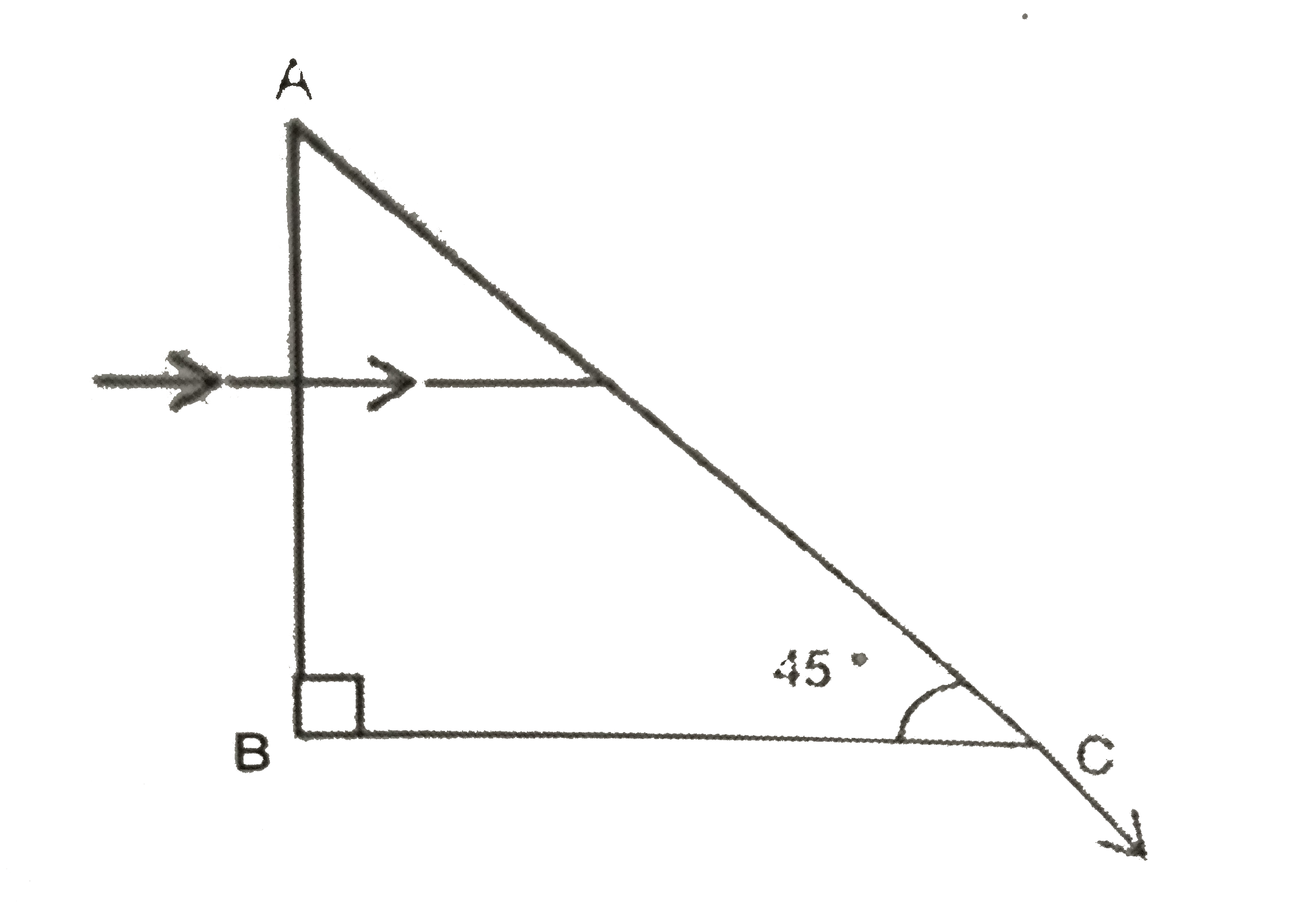 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In figure, ABC is the cross section of a right-angled prism and ACDE is the cross section of a gless slab. The value of θ so that light incident normally on the face AB does not cross the face AC is (given sin−1(3/5)=37∘).
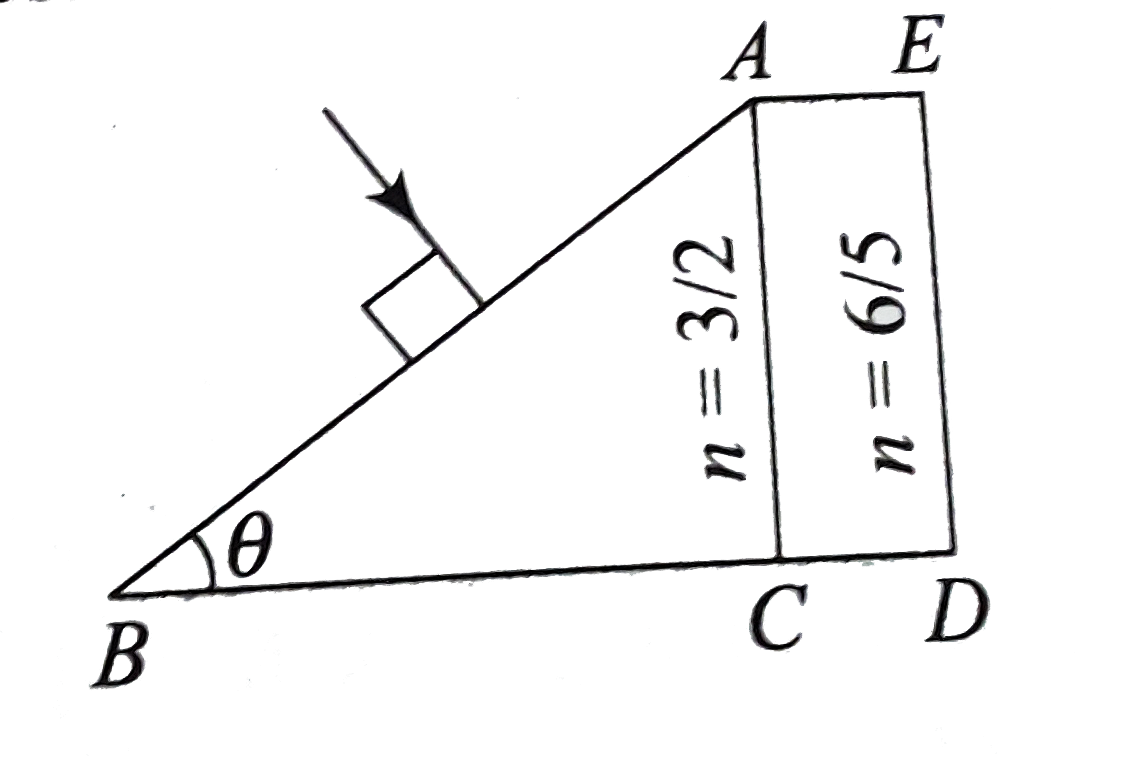 Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘
Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘ - Question 2 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if
 Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these
Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these - Question 3 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.
 Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
What should be the value of angle θ so that light entering normally through the surface AC of a prism (n=3/2) does not cross the second refracting surface AB?
 View Solution
View SolutionWhat should be the value of angle so that light entering normally through the surface AC of a prism (n = 3/2) does not cross the second refracting surface AB.
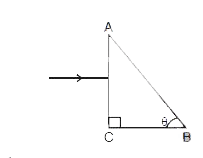 View Solution
View SolutionFigure shows a right angled prism ABC having refractive μg=32 lowered into water (μω43). Find angle α so that the incident ray normal to face AB will be reflected at face BC completely.
 View Solution
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
 .View Solution
.View SolutionAn equilateral triangular prism is made of glass (μ=1.5). A ray of light is incident normally on one of the faces. The angle between the incident and emergent ray is
View Solution

