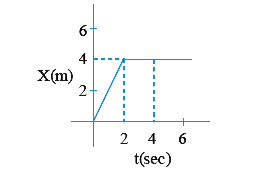
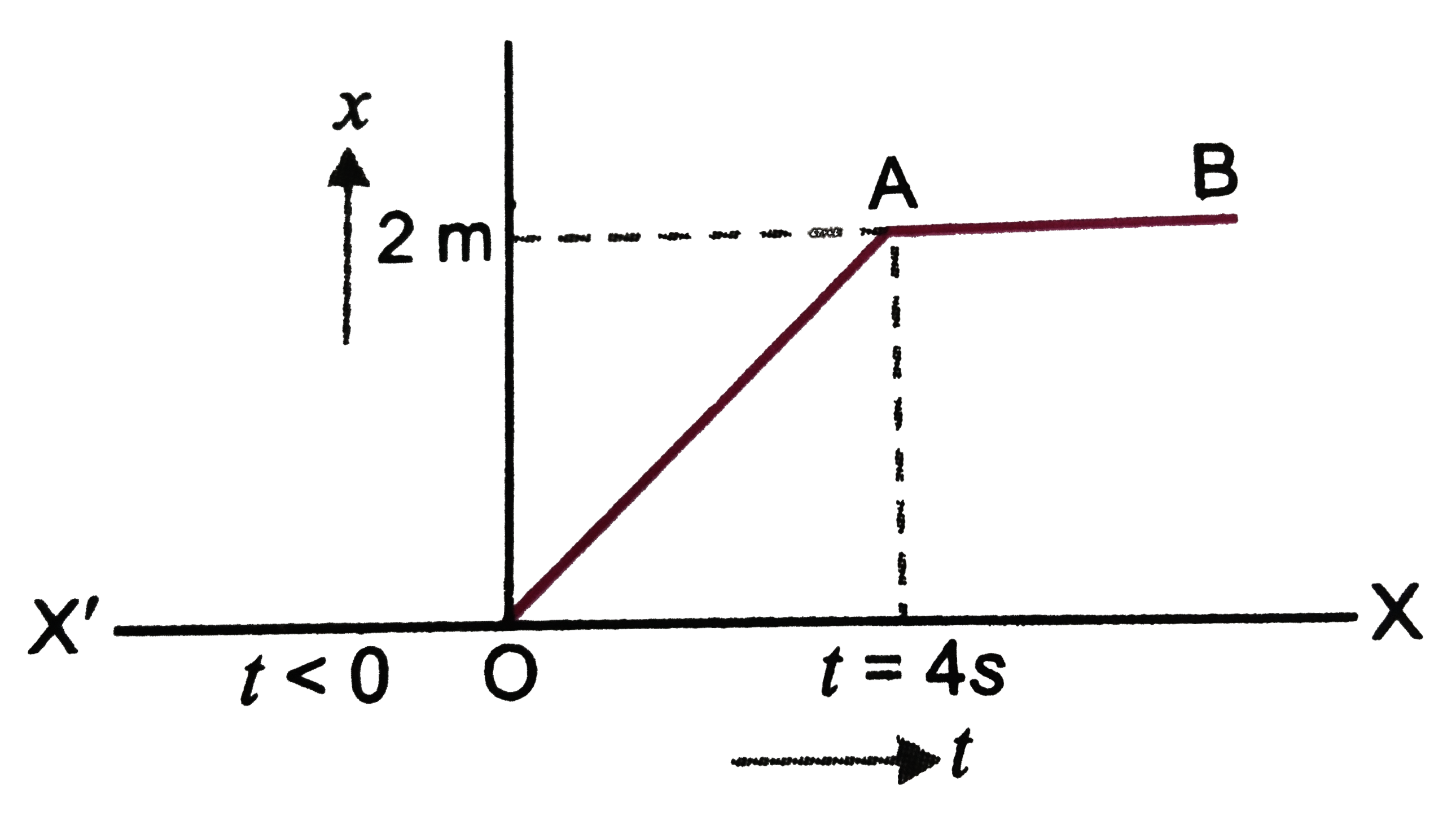
In the figure given below, the position-time graph of a particle of mass $0.1 k g$ is shown. The impuslse at $t = 2$ sec is

A

$0.2 k g m s^{- 1}$

B

$- 0.2 k g m s^{- 1}$

C

$0.1 k g m s^{- 1}$

D

$- 0.4 k g m s^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

If a constant force $F$ is applied on a body for a short interval of time $Δ t$ , then impulse of this force is $F \times Δ t$ . From Newton's second law.
$F = m a = m \frac{Δ v}{Δ t}$
$\Rightarrow F Δ t = m Δ v = Δ p$
$∴$ Impulse, $I = Δ_{p} = m \frac{Δ x}{Δ t}$
Given, $m = 0.1 k g, \frac{Δ x}{Δ t} = \frac{4}{2} m / s$
$∴ I = 0.1 \times \frac{4}{2} = 0.2 k g m s^{- 1}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS MOCK TEST

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
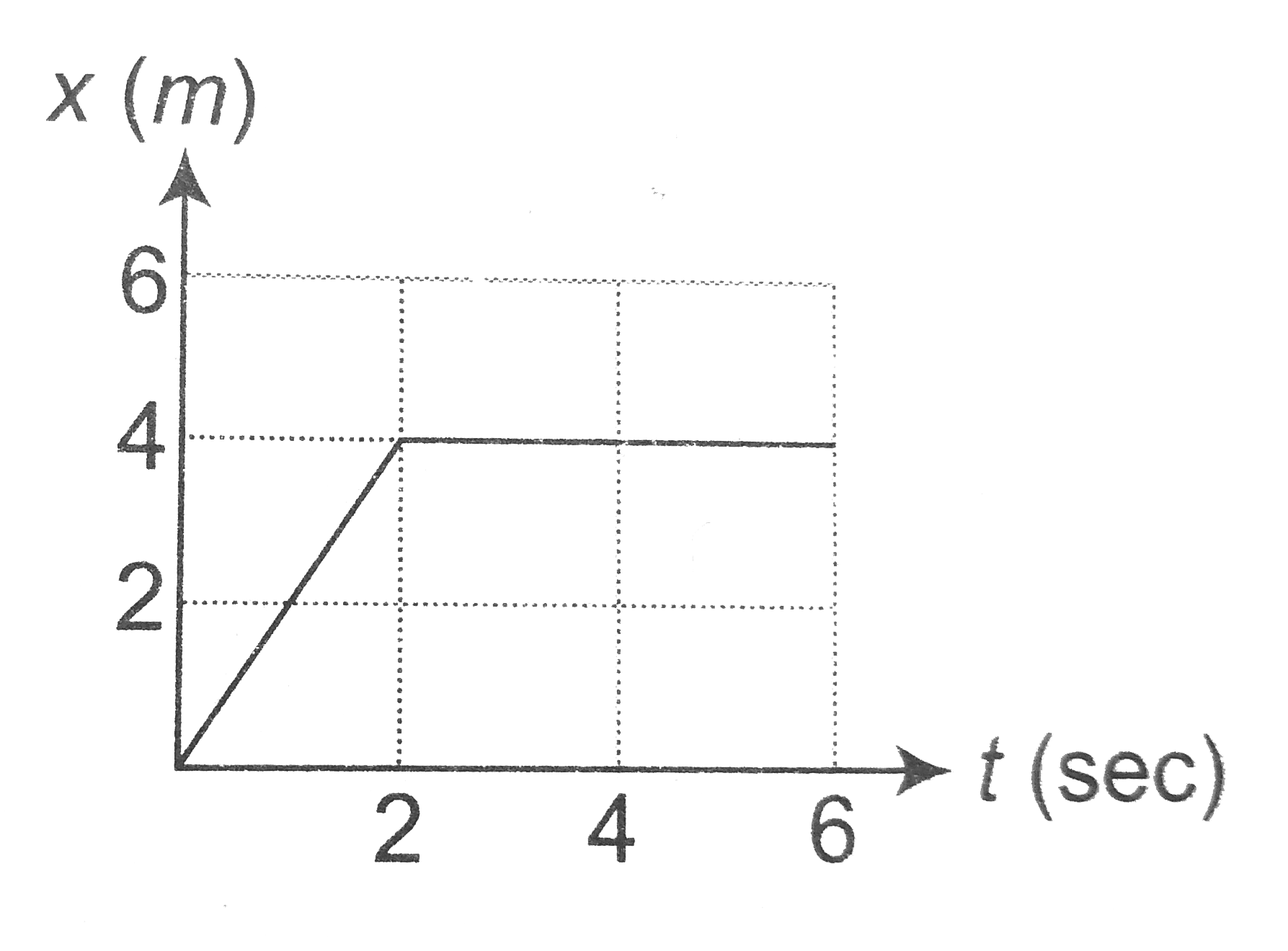
In the figure given below, the position time graph of a particle of mass 0.1kg is shown. The impulse at t=2 sec is

A $0.2 g k m / sec$
B $- 0.2 k g m {sec}^{- 1}$
C $0.1 k g m {sec}^{- 1}$
D $- 0.1 k g m / sec$
Question 2 - Select One
In the figure given below, the position–time graph of a particle of mass 0·1 kg is shown. The impulse at $t = 2 sec$ is

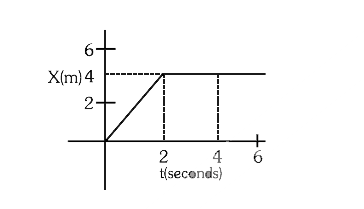A $0 \cdot 2 {kgmsec}^{- 1}$
B $- 0 \cdot 2 {kgmsec}^{- 1}$
C $0 \cdot 1 {kgmsec}^{- 1}$
D $- 0 \cdot 4 {kgmsec}^{- 1}$
Question 3 - Select One
In the figure given, the position-time graph of a particle of mass 0.1 kg is shown the impulse at t = 2s is
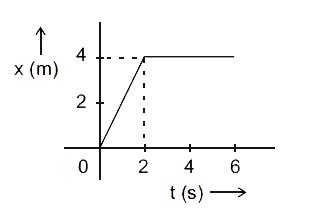A0.2 kg m/s
B $- 0.2$ kg m/s
C0.1 kg m/s
D $- 0.4$ kg m/s

A2Z-MOCK TEST-General Kinematics

Home
Ask Doubt
Profile