In the figure shown A, B and C are three points on the circumference of a disc. Let vA,vB and vc are speeds of these three points then
vc>vB>vA
Reason: In case of rotaional plus translational motion of a rigid body, net speed of any point (other than centre of mass) is greater than, less than or equal to the speed of centre of mass.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If assertion is true, but the reaction is false.
If assertion is false but the reason is true.
At C two terms v and Rωare 0∘ at A they are at 180∘ and a B they are at 90∘
∴vC=v+Rω
vA=v−Rω
and vB=√v2+(Rω)2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.11
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
Two particles A and B (both initially at rest) start moving towards each other under a mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2v, the speed of the centre of mass is
AzeroBvC3v2D−3v2For the network shown in figure, points A, B and C are at potentials of 70 V, zero and 10 V respectively
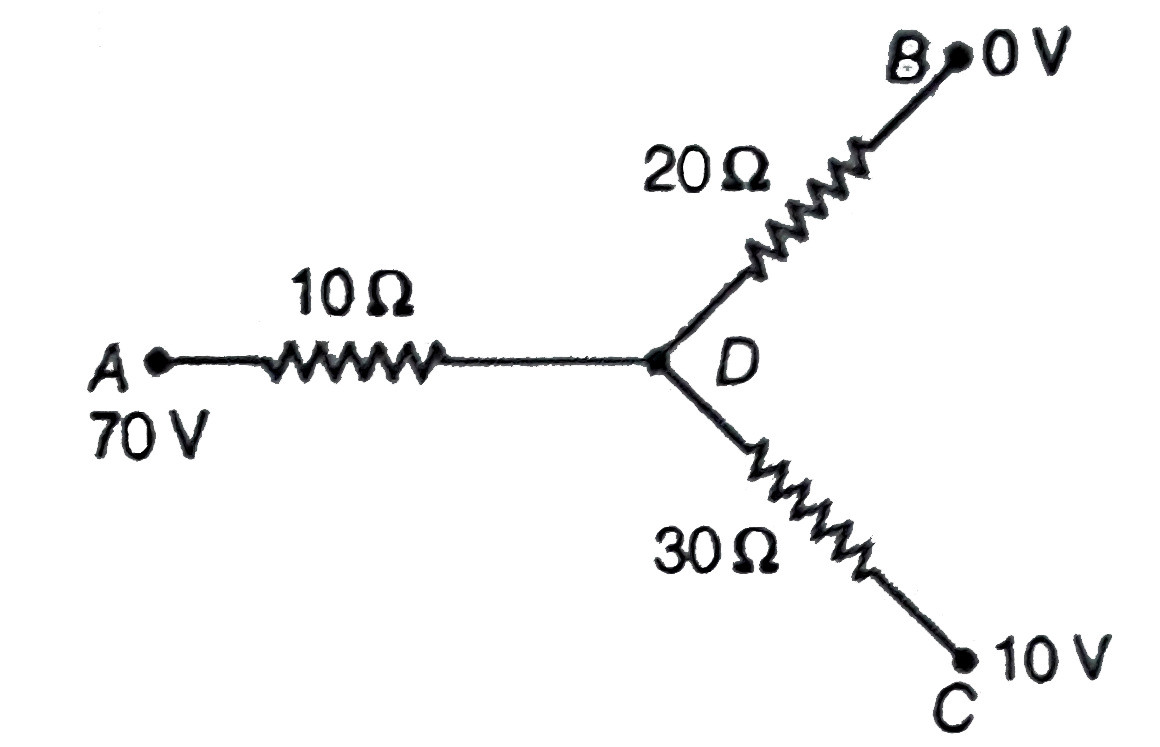 Apoint D is at a potential of 40 VBthe currents in the sections AD, DB and DC are in the ratio 4:3:2Cthe current in the sections AD, DB and DC are in the ratio 1:2:3Dthe network draws a total power of 100 W
Apoint D is at a potential of 40 VBthe currents in the sections AD, DB and DC are in the ratio 4:3:2Cthe current in the sections AD, DB and DC are in the ratio 1:2:3Dthe network draws a total power of 100 W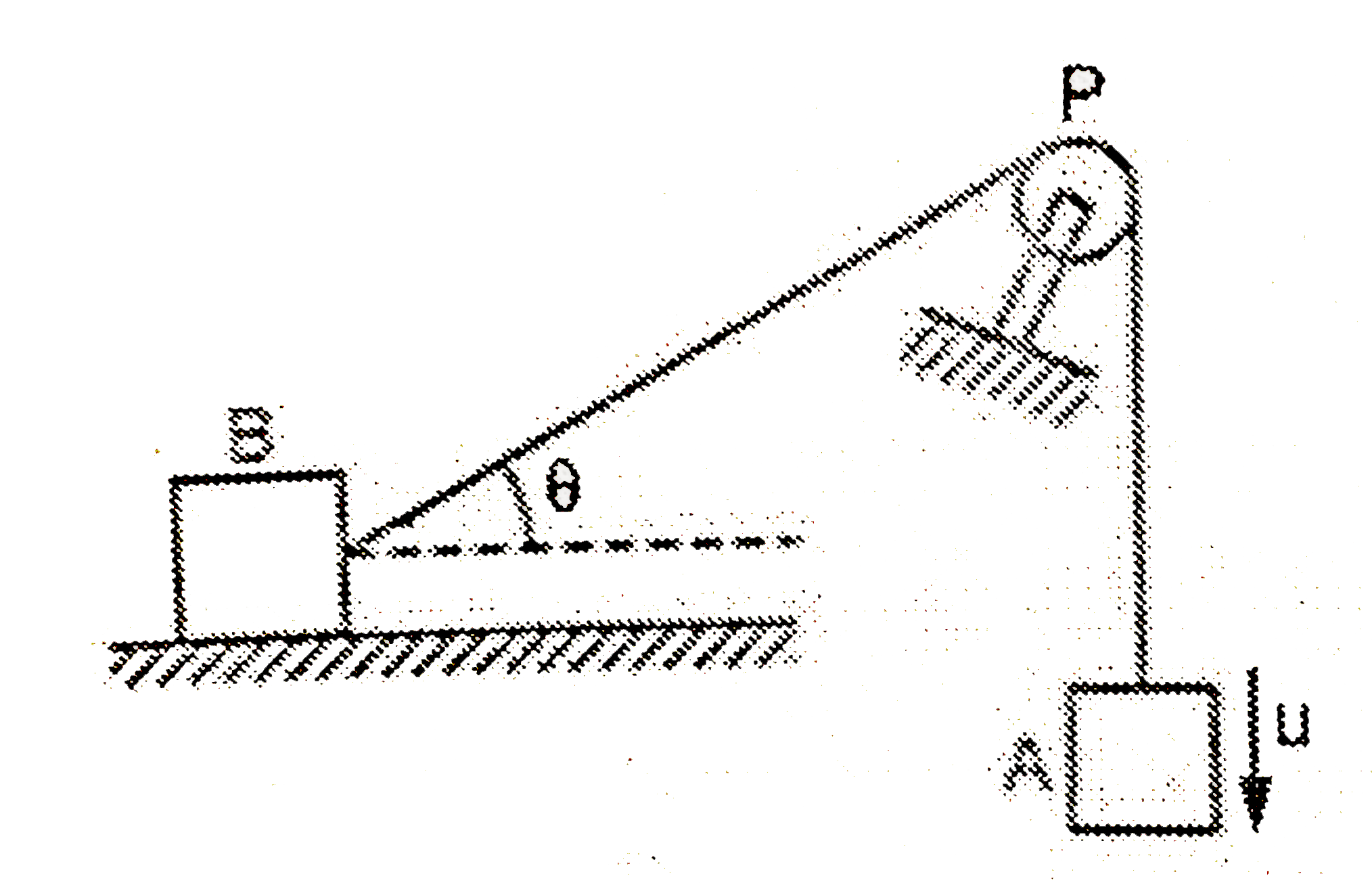
In the figure, the blocks are of equal mass. The pulley is fixed. In the position shown, A moves down with a speed u, and vB= the speed of B.AB will never lose contact with the groundBThe downward acceleration of A is equal in magnitude to the horizontal acceleration of BCvB=ucosθDuB=u/cosθ
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
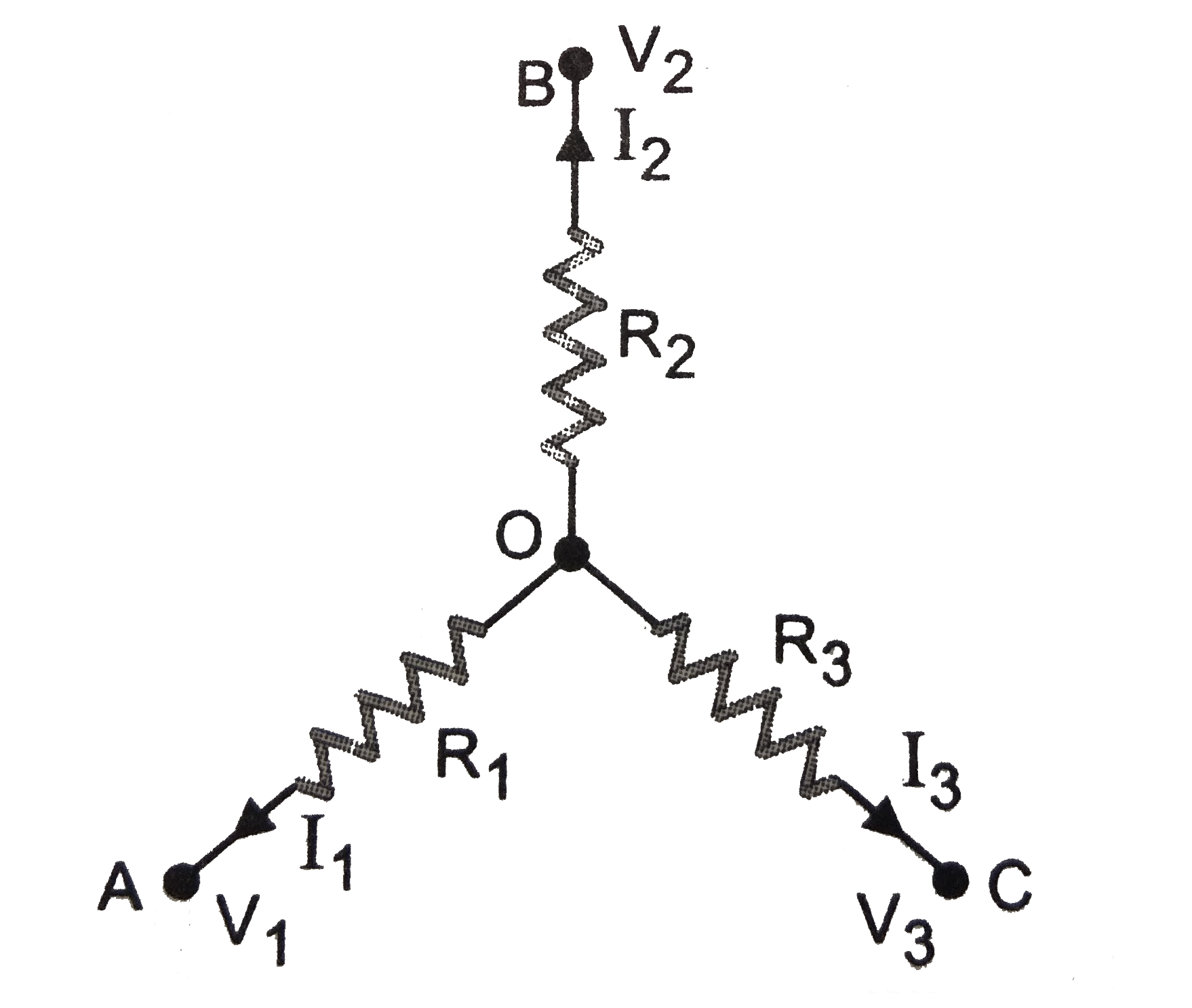
View Solution
Point C is the centre of mass of the rigid body shown in figure. Find the total torque acting on the body about point C.
View SolutionA wheel is rolling uniformly along a level road (see figure). The speed of transitional motion of the wheel axis is V. What are the speeds of the points A and B on the wheel rim relative to the road at the instant shown in the figure?
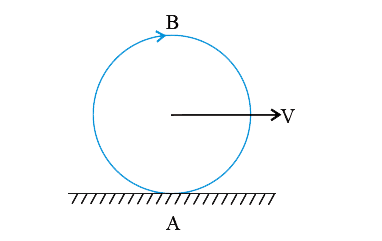
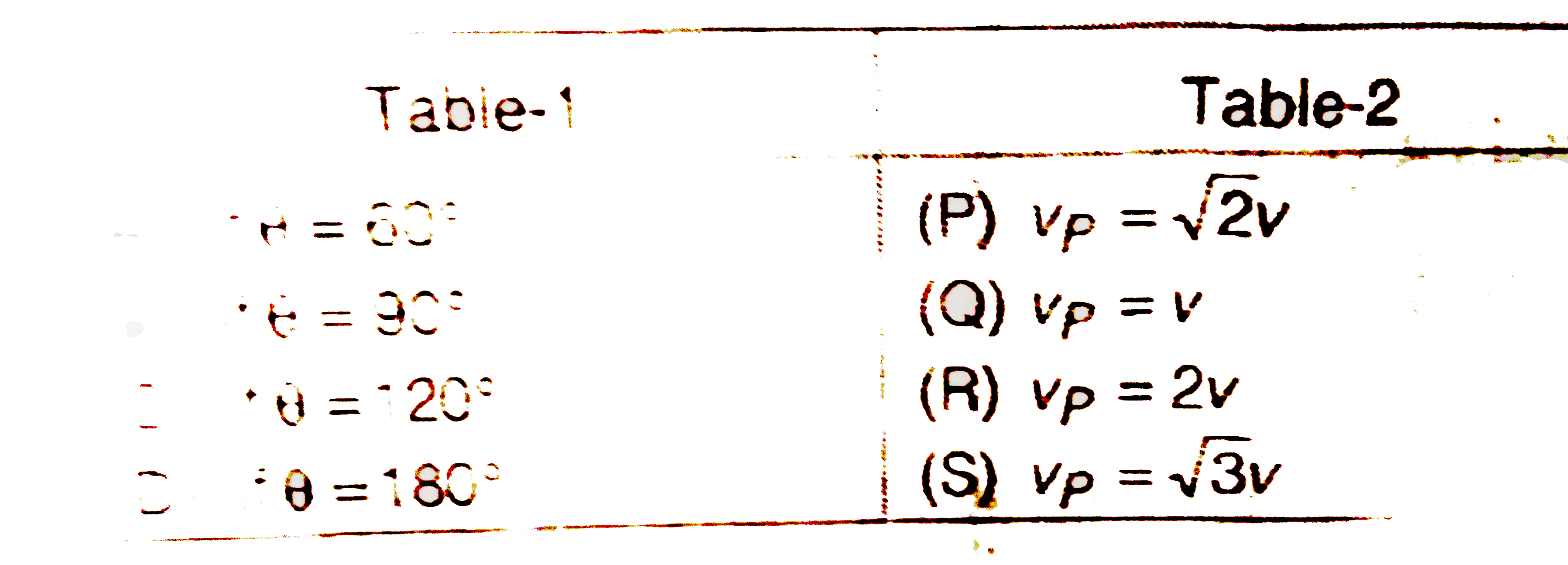
View SolutionA disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View Solution