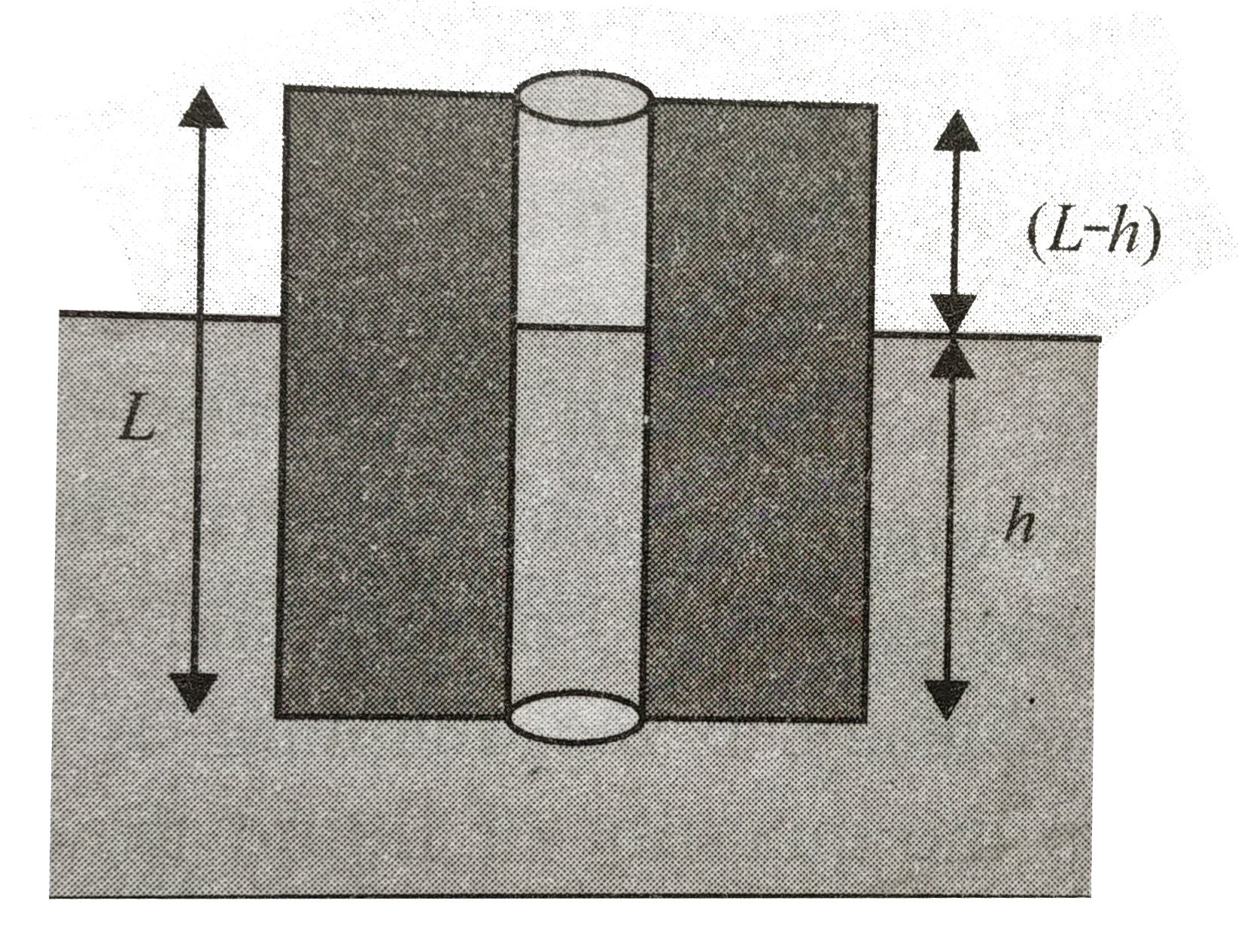
In the middle of a pond, a large ice block of 10 m thickness of floating. Let a vertical hole is drilled in this block. The minimum length (in cm) of a rope required to lift a bucket full of water through the hole is x×10cm? (Specify gravity of ice =0.91).
To solve the problem, let's break it down step by step:
Step 1: Understand the Problem
We have a large ice block floating in a pond with a thickness of 10 meters. A vertical hole is drilled in this block, and we need to find the minimum length of a rope required to lift a bucket full of water through this hole.
Step 2: Define Variables
- Let t be the thickness of the ice block, which is given as t=10 m.
- Let y be the height of the ice block above the water surface.
- The specific gravity of ice is given as 0.91.
Step 3: Use the Concept of Buoyancy
In equilibrium, the weight of the ice block is equal to the buoyant force acting on it. The buoyant force is equal to the weight of the water displaced by the submerged part of the ice.
Step 4: Write the Equilibrium Condition
The weight of the ice block W can be expressed as:
W=ρice⋅Vice⋅g=ρice⋅A⋅t⋅g
The buoyant force FB can be expressed as:
FB=ρwater⋅Vdisplaced⋅g=ρwater⋅A⋅(t−y)⋅g
Setting these two equal gives:
ρice⋅A⋅t⋅g=ρwater⋅A⋅(t−y)⋅g
Step 5: Cancel Common Terms
Since A and g are common on both sides, we can cancel them out:
ρice⋅t=ρwater⋅(t−y)
Step 6: Rearrange the Equation
Rearranging gives:
ρwater⋅t−ρwater⋅y=ρice⋅t
ρwater⋅y=ρwater⋅t−ρice⋅t
y=t⋅(1−ρiceρwater)
Step 7: Substitute Specific Gravity
The ratio of densities can be expressed in terms of specific gravity:
ρiceρwater=Specific Gravity of Ice=0.91
Thus,
y=t⋅(1−0.91)=t⋅0.09
Step 8: Calculate y
Substituting t=10 m:
y=10⋅0.09=0.9 m
Step 9: Convert to Centimeters
To find the minimum length of the rope required in centimeters:
y=0.9 m=0.9×100 cm=90 cm
Step 10: Final Answer
The minimum length of the rope required to lift the bucket full of water through the hole is 90 cm. In the form x×10 cm, we have x=9.
We have a large ice block floating in a pond with a thickness of 10 meters. A vertical hole is drilled in this block, and we need to find the minimum length of a rope required to lift a bucket full of water through this hole.
- Let t be the thickness of the ice block, which is given as t=10 m.
- Let y be the height of the ice block above the water surface.
- The specific gravity of ice is given as 0.91.
In equilibrium, the weight of the ice block is equal to the buoyant force acting on it. The buoyant force is equal to the weight of the water displaced by the submerged part of the ice.
The weight of the ice block W can be expressed as:
W=ρice⋅Vice⋅g=ρice⋅A⋅t⋅g
The buoyant force FB can be expressed as:
FB=ρwater⋅Vdisplaced⋅g=ρwater⋅A⋅(t−y)⋅g
Setting these two equal gives:
ρice⋅A⋅t⋅g=ρwater⋅A⋅(t−y)⋅g
Since A and g are common on both sides, we can cancel them out:
ρice⋅t=ρwater⋅(t−y)
Rearranging gives:
ρwater⋅t−ρwater⋅y=ρice⋅t
ρwater⋅y=ρwater⋅t−ρice⋅t
y=t⋅(1−ρiceρwater)
The ratio of densities can be expressed in terms of specific gravity:
ρiceρwater=Specific Gravity of Ice=0.91
Thus,
y=t⋅(1−0.91)=t⋅0.09
Substituting t=10 m:
y=10⋅0.09=0.9 m
To find the minimum length of the rope required in centimeters:
y=0.9 m=0.9×100 cm=90 cm
The minimum length of the rope required to lift the bucket full of water through the hole is 90 cm. In the form x×10 cm, we have x=9.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Matching Type Questions )
2 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum length of the rope required to scoop out a bucket full of water through the hole is (0.2x)m. Find the value of x. Take density of ice =0.9 g/cm3
View SolutionA large block of ice 5m thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice =0.9.
View Solution
Knowledge Check
A large block of ice 4 m thick has a vertical hole drilled through it and is floating in the middle of water in a lake. The minimum length of rope required to scoop up a bucket full of the through the hole is (density of ice =0.9CGS unit, density of water =1CGS unit)
A40 cmB24 cmC20 cmD360 cmThe thickness of the ice layer on the surface of lake is 20 m. A hole is made in the ice layer. What is the minimum length of the rope required to take a bucket full of water out ? (Take density of ice =0.9×103kg/m3)
A2 mB5 mC9 mD18 mA large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice =0.9gcm−3)
A0.5 mB1.0 mC1.2 mD1.8 m
A large block of ice cuboid of height 'l' and density ρice=0.9ρw' has a large vertical hole along its axis. This block is floating in a lake. Find out the length of the rope required to raise a bucket of water through the hole.
View SolutionDue to cold weather a 1 m water pipe of cross-sectional area 1cm2 is filled with ice at −10∘C. Resistive heating is used to melt the ice. Current of 0.5 A is passed through 4kΩ resistance. Assuming that all the heat produced is used for melting, what is the minimum time required ?
(Given latent heat of fusion for water/ice =3.33×105Jkg−1,
specific heat of ice =2×103Jkg−1 and
density of ice =103kg/m3)
View SolutionDue to cold weather a 1 m water pipe of cross-sectional area 1cm2 is filled with ice at −10∘C. Resistive heating is used to melt the ice. Current of 0.5 A is passed through 4kΩ resistance. Assuming that all the heat produced is used for melting, what is the minimum time required ?
(Given latent heat of fusion for water/ice =3.33×105Jkg−1,
specific heat of ice =2×103Jkg−1 and
density of ice =103kg/m3)
View SolutionA large block of ice cuboid of edge length 'l' and density ρice−0.9ρw, has a larger vertical hole along its axis. This block is floating in a lake. Find out length of the rope required to raise a bucket of water through the hole.
View SolutionAn ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
View Solution
