In the previous problem , if the collision is head - on elastic , find (a) the velocities of balls immediately after the collision and (b) the maximum height attained by eacl ball.
(a) 
By the momentum conservation
m√2gL+2m×0=mv1+2mv2 (i)
v1+√2gL=v2+0 (ii)
Solving , v1=−13√2gL,v2=2m√2gL
(b) 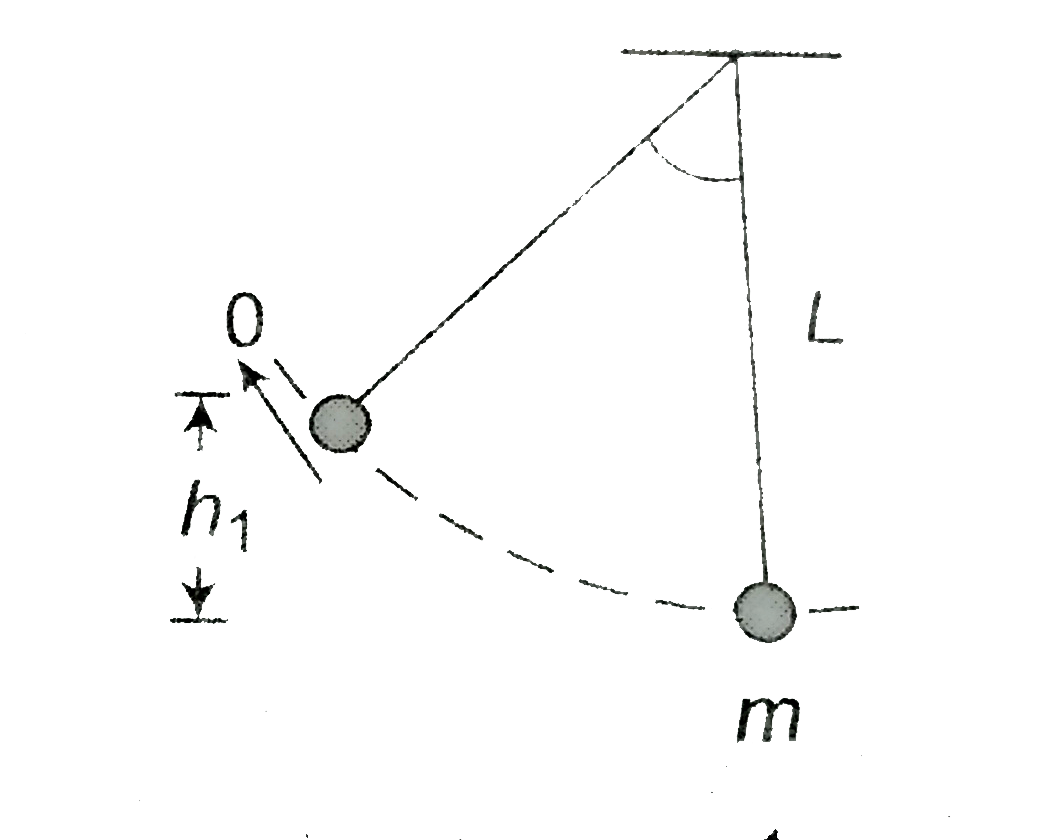
0=v21−2gh1⇒0=19×2gL−2gh1
⇒h1=L9
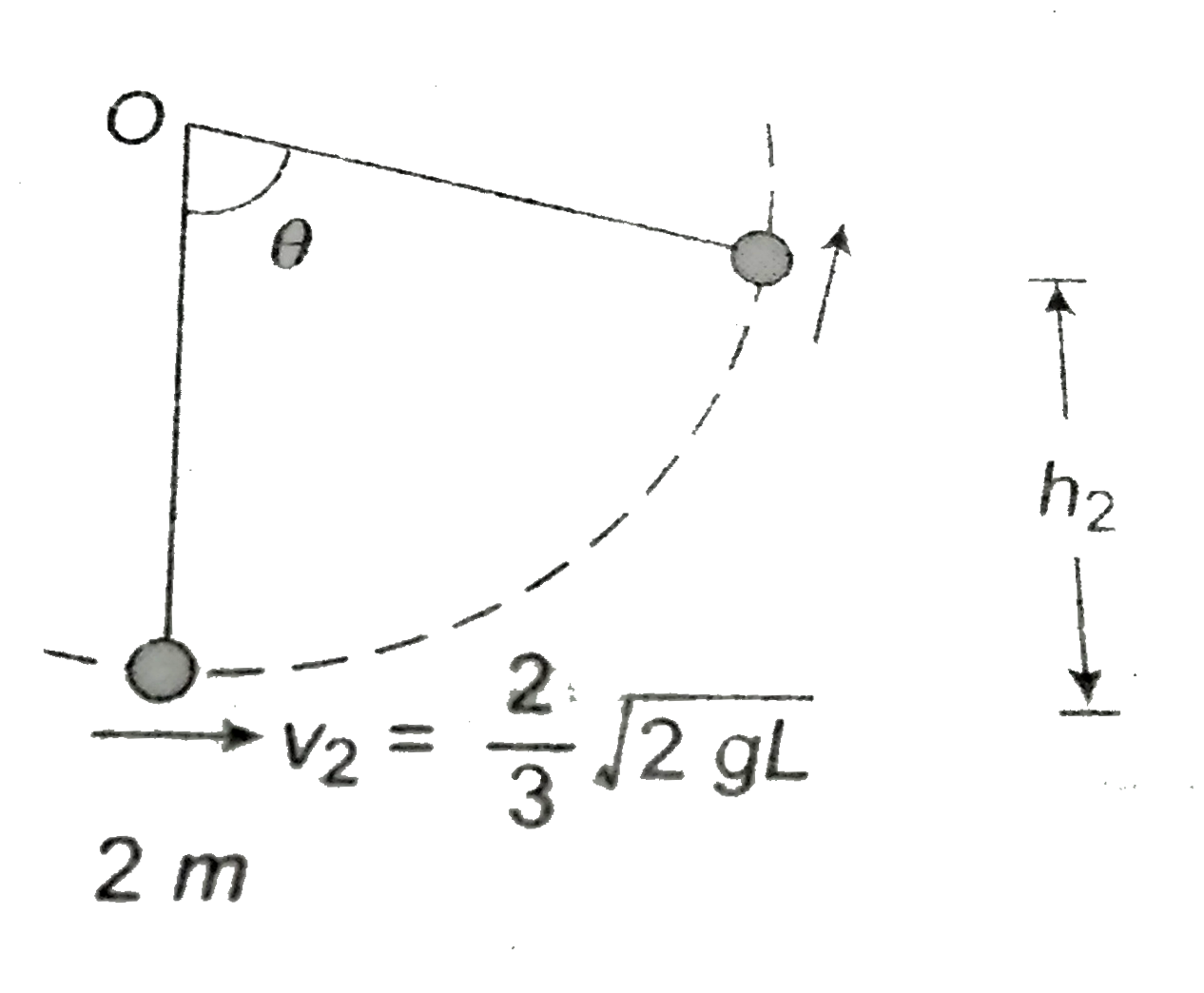
0=v22−2gh2⇒0=49×2gL−2gh2
⇒h2=4L9
Topper's Solved these Questions
Similar Questions
A ball is dropped from a height h on a floor if the coefficient of restitution ise. Find the
(a). Speed of ball after the first second … nth collision.
(b). Maximum height attained by the ball, after the first, second … nth collision.
(c). Time taken by the ball to reach the highest point after the first, second, ...nth collision.
(d). total distance covered by the ball.
(e). totol time of journey.
View SolutionThe velocities in a head on elastic collision be interchanged"
View Solution
Knowledge Check
In the previous problem , time taken by the ball up to the third collision
A3sB4sC5sD6sIn the previous problem , the maximum height attained by the ball and the distance traveled by the block , after collision will be
A2L9,4L9B4L3,L3C4L9,L9DL9,2L9The ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision
 A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
A ball of mass m moving with velocity u strikes another identical ball at rest. Find the velocities of the balls after the collision if the coefficient of restitution is e and the collision is head -on. Also , calculate the loss in K.E.
View SolutionA smooth ball of mass M and radius R is lying on a smooth horizontal table. A smaller ball of radius r and mass m travelling horizontally on the table with velocity u hits the larger ball. Collision is elastic. During the interaction of the balls the larger ball does not lose contact with the table at any instant

(i) Calculate the velocity of the balls after collision.
(ii) Calculate the maximum possible interaction force between the balls during collision.
View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionRod can rotate about hinge point 'P'. A ball of mass 'm' is projected with a velocity 5v0 in a gravity free space as shown in figure. Collision between the rod and the ball is perfectly elastic. Then find the magnitude of velocity of ball after the collision ( neglect the friction between the ball and the rod during the collision ).
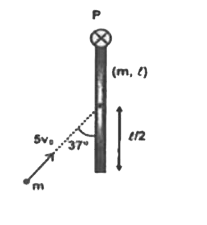
View SolutionConsider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
View Solution
