Consider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
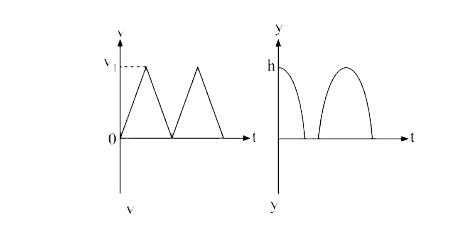
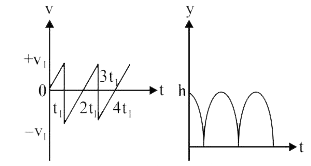
The correct Answer is:C
To solve the problem of a rubber ball falling from a height of 4.9 m onto a horizontal elastic plate, we need to determine the velocity and height of the ball as functions of time. We will consider the motion of the ball before and after the collision with the plate.
1. Determine the time taken to fall to the plate:
The ball is dropped from a height h=4.9m. Using the equation of motion:
h=12gt2
where g is the acceleration due to gravity (approximately 9.8m/s2). Rearranging gives:
t2=2hg=2×4.99.8=1⟹t=1s
Hint: Use the equation of motion for free fall to find the time taken to reach the ground.
2. Calculate the velocity just before impact:
The velocity of the ball just before it hits the plate can be calculated using:
v=gt
Substituting t=1s:
v=9.8×1=9.8m/s
Hint: Use the formula for velocity under constant acceleration to find the speed just before impact.
3. Analyze the collision:
Since the collision is perfectly elastic, the ball will rebound with the same speed but in the opposite direction. Thus, the velocity after the collision will be:
vafter=−9.8m/s
Hint: Remember that in a perfectly elastic collision, the speed remains the same, but the direction reverses.
4. Determine the height as a function of time after the collision:
After the collision, the ball will ascend back to the height of 4.9 m. The time taken to reach the maximum height can be found using:
v=u+at
where u=−9.8m/s (upward), v=0 (at the maximum height), and a=−g:
0=−9.8−9.8t⟹t=1s
Thus, it takes another 1 second to reach the maximum height.
5. Height as a function of time:
The height h(t) can be modeled as:
- For 0≤t<1:
h(t)=4.9−12gt2
- For 1≤t<2:
h(t)=4.9+12g(t−1)2
Hint: Use the equations of motion to describe the height during both the falling and rising phases.
6. Velocity as a function of time:
The velocity v(t) can be described as:
- For 0≤t<1:
v(t)=−gt
- For 1≤t<2:
v(t)=−9.8+g(t−1)
Hint: Use the equations of motion to describe the velocity during both the falling and rising phases.
Summary:
- Velocity as a function of time:
v(t)={−9.8tfor 0≤t<19.8(t−1)for 1≤t<2
- Height as a function of time:
h(t)={4.9−12gt2for 0≤t<14.9+12g(t−1)2for 1≤t<2
The ball is dropped from a height h=4.9m. Using the equation of motion:
h=12gt2
where g is the acceleration due to gravity (approximately 9.8m/s2). Rearranging gives:
t2=2hg=2×4.99.8=1⟹t=1s
The velocity of the ball just before it hits the plate can be calculated using:
v=gt
Substituting t=1s:
v=9.8×1=9.8m/s
Since the collision is perfectly elastic, the ball will rebound with the same speed but in the opposite direction. Thus, the velocity after the collision will be:
vafter=−9.8m/s
After the collision, the ball will ascend back to the height of 4.9 m. The time taken to reach the maximum height can be found using:
v=u+at
where u=−9.8m/s (upward), v=0 (at the maximum height), and a=−g:
0=−9.8−9.8t⟹t=1s
Thus, it takes another 1 second to reach the maximum height.
The height h(t) can be modeled as:
- For 0≤t<1:
h(t)=4.9−12gt2
- For 1≤t<2:
h(t)=4.9+12g(t−1)2
The velocity v(t) can be described as:
- For 0≤t<1:
v(t)=−gt
- For 1≤t<2:
v(t)=−9.8+g(t−1)
- Velocity as a function of time:
v(t)={−9.8tfor 0≤t<19.8(t−1)for 1≤t<2
h(t)={4.9−12gt2for 0≤t<14.9+12g(t−1)2for 1≤t<2
Similar Questions
A ball falls from a height 20m on to a horizontal plane and rebound to a height of 5/64m after 4 collisions.Find the coefficient of restitution.
View SolutionA ball falls from a height of 5m on to a horizontal plane.If the coefficient of restitution is 0.4, the height to which it rebounds after 2 collisions is approximately
View Solution
Knowledge Check
- Question 1 - Select One
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
A12sB1sC32sD34s - Question 2 - Select One
A plastic ball falling from a height 4.9m rebounds number of times. If total time for second collision is 2.4sec, then coefficient of restitution is
A0.3B0.4C0.7D0.6 - Question 3 - Select One
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
A rubber ball dropped from a height of 20m(g=10ms2) falls on the roof of an elevator going up at 2m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of?
View SolutionA rubber ball dropped from a height of 20m (g=10ms2) falls on the roof of an elevator going up at 2m/s .If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of
View SolutionA steel ball of mass 0.5 kg is dropped from a height of 4 m on to a horizontal heavy steel slab. The collision is elastic and the ball rebounds to its original height.
Calculate the impulse delivered to the ball during impact.View SolutionA metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
View SolutionA ball falls from a height of 10m on to a horizontal plane. If the coefficient of restitution is 0.4, then the velocity with which it rebounds from the plane after second collision is
View Solution

