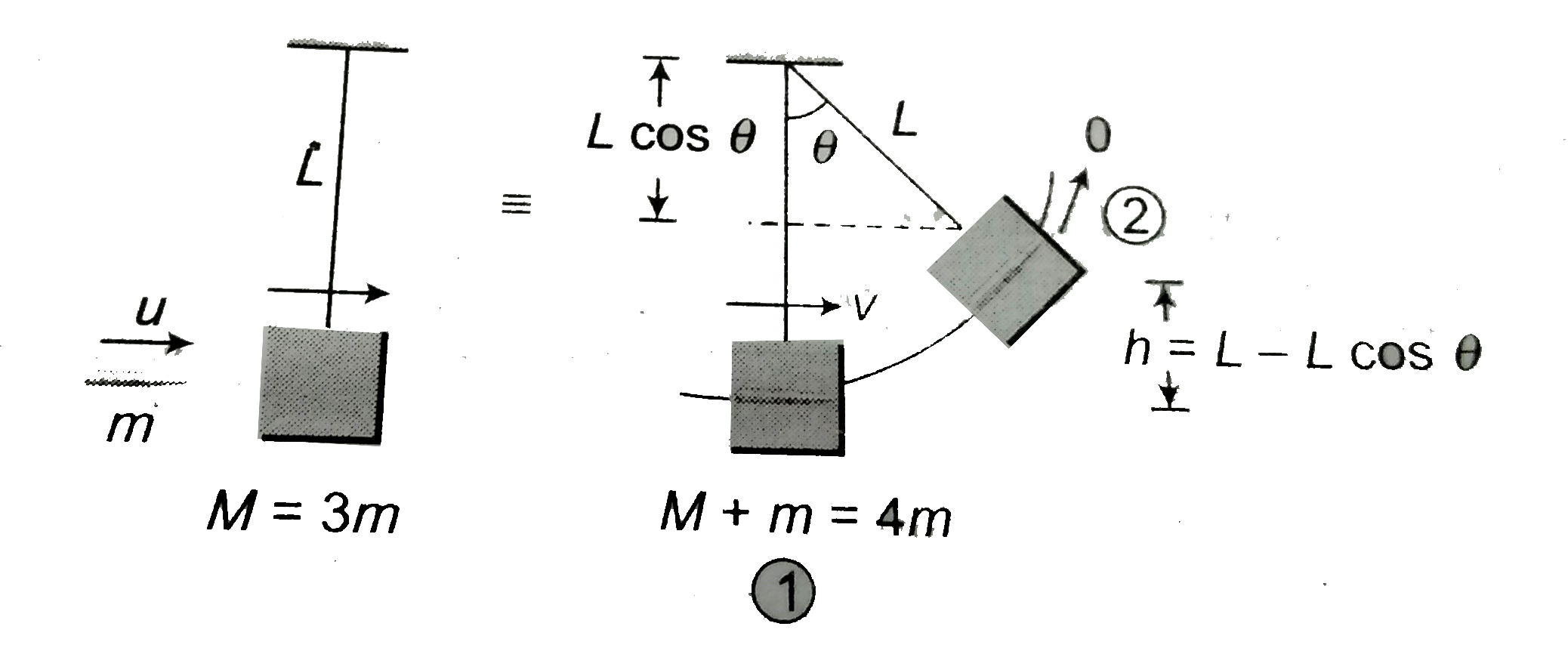
In the previous problem , the block of massM is attached to a string of length L. Find the maximum angle made by the string with vertical . Take veloctiy of buller u=4√gL. Take M=3m.
By the momentum conservation
mu+M×0=(m+M)V
V=muM+m=u4=4√gL4=√gL
Since V<√2gL
Therefore , the combined mass will oscillate like a simple pendulum , hence , the maximum angle θ<90∘.
Between (1) and (2)
0=V2−2gh
h=V22g
L(1−cosθ)=gL2g=L2⇒cosθ=12⇒θ=60∘
Topper's Solved these Questions
Similar Questions
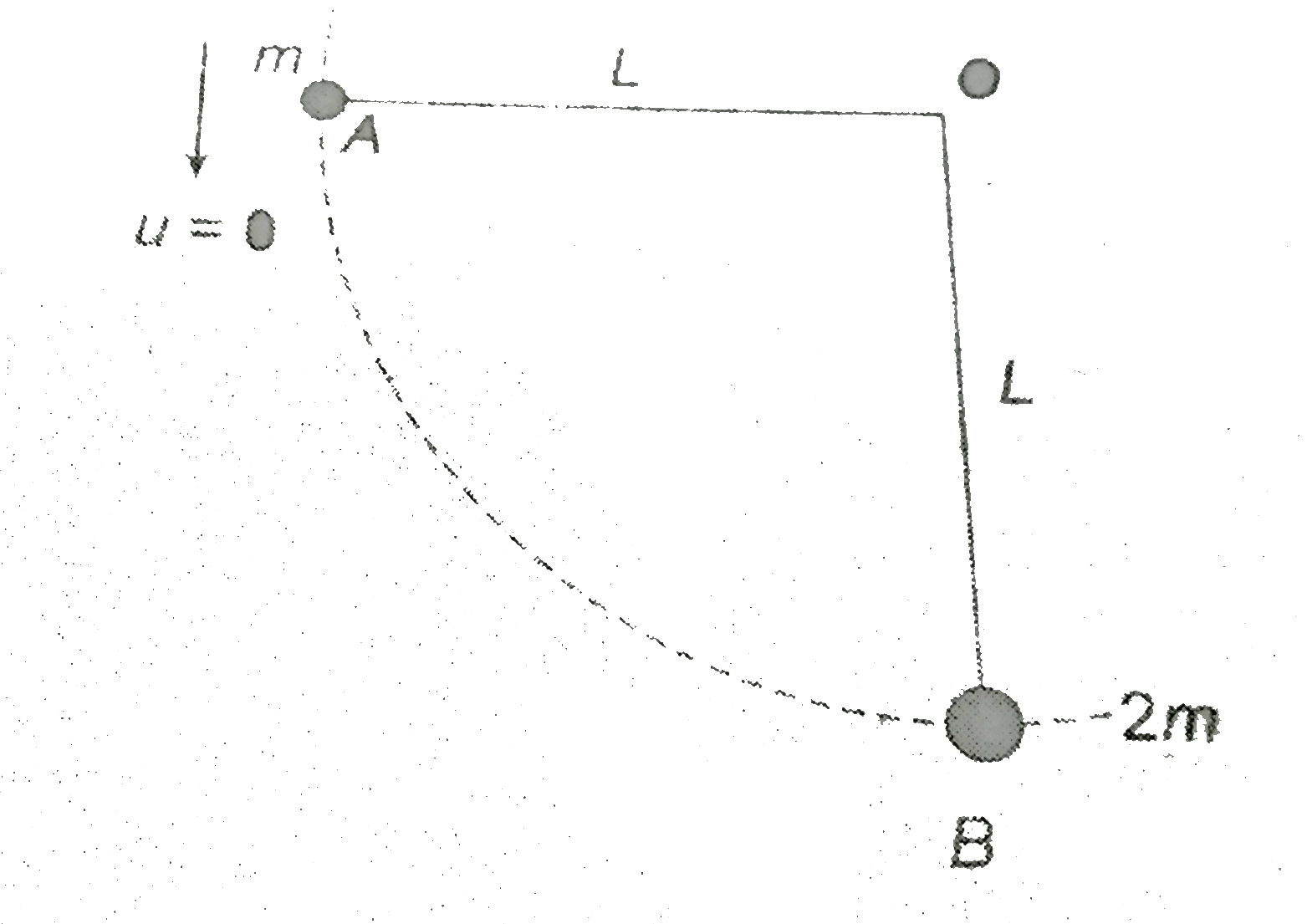
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
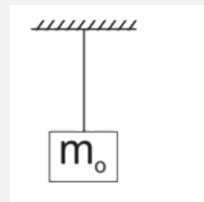
View SolutionThe block of mass m0=μL is attached to a uniform string of mass M=μL and length L as shown in the figure. If a wave pulse is produced near the block, then the time it taken to reach the ceiling is
View Solution
Knowledge Check
- Question 1 - Select One
In the previous problem. If the bullet is moving with velocity 50√2m/s, the maximum angle made by string with vertical is
A60∘B45∘Csin−1(45)Dcos−1(45) - Question 2 - Select One
The block of mass m is at rest. Find the tension in the string A .
AmgB2 mgC3 mgD4 mg - Question 3 - Select One
A stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
ARadially outwardBRadialy inwardCTangentially outwardDWith acceleration mv2l
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA ball of mass M is rotating in a conical pendulum by a string of length L. If radius of circular path is L√2, find the velocity of mass
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
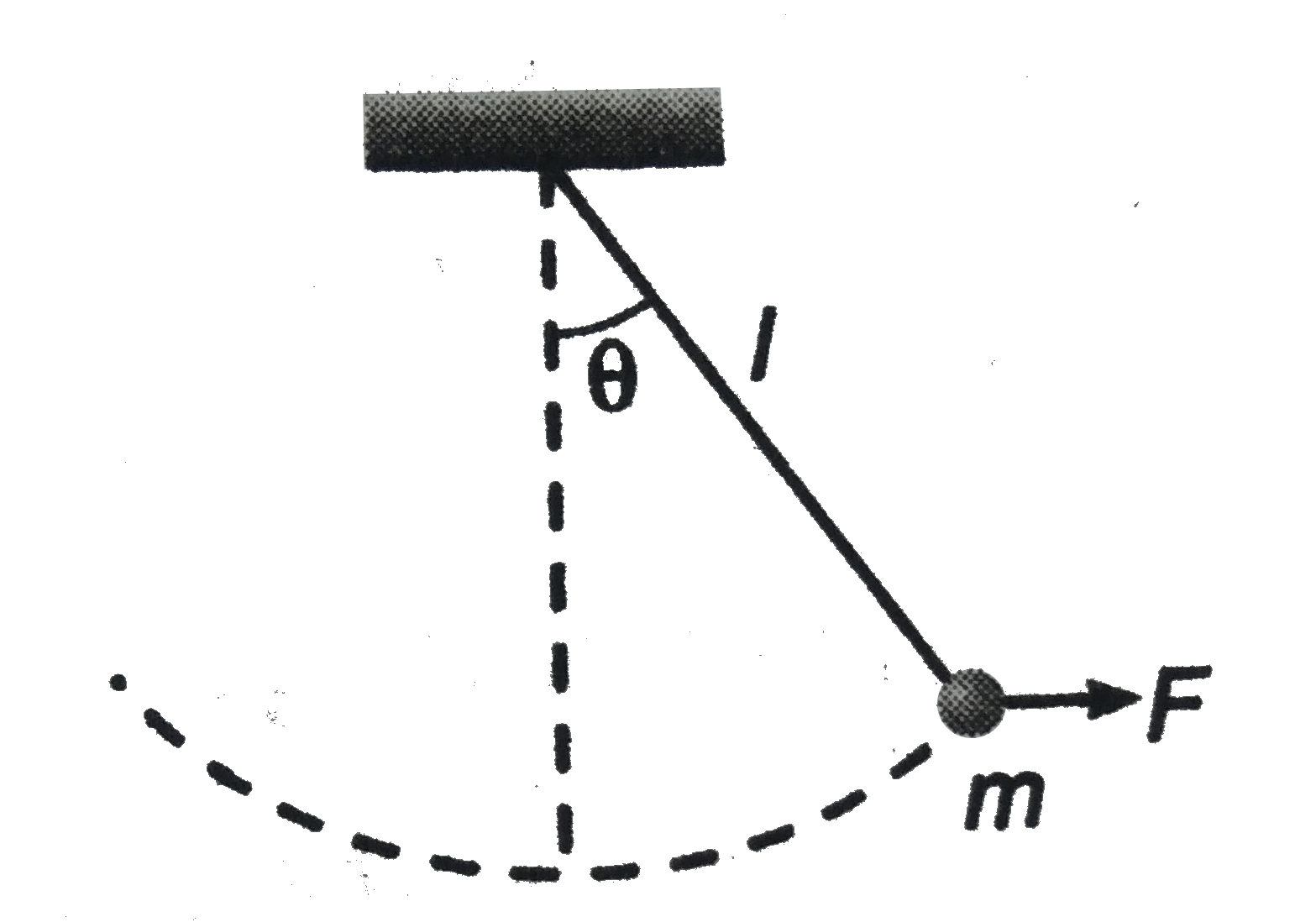
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
. View Solution