In the previous question, if a>μsg, find the work done by friction on the block during time t.
To find the work done by friction on the block during time t, we can follow these steps:
Step 1: Identify the forces acting on the block
The block experiences a kinetic friction force when it slides over the surface. The frictional force can be expressed as:
Ffriction=μkmg
where μk is the coefficient of kinetic friction, m is the mass of the block, and g is the acceleration due to gravity.
Step 2: Determine the net acceleration of the block
The net force acting on the block can be expressed as:
Fnet=Ffriction−Fapplied=μkmg−ma
where a is the acceleration of the block relative to the ground. Rearranging gives:
μkmg=ma+ma1
where a1 is the acceleration of the block with respect to the plank.
Step 3: Calculate the acceleration of the block
From the previous equation, we can express the acceleration a2 (the net acceleration of the block with respect to the ground) as:
a2=μkg−am
Step 4: Calculate the displacement of the block during time t
The displacement s of the block during time t can be calculated using the formula for displacement under uniform acceleration:
s=12a2t2
Step 5: Calculate the work done by friction
The work done W by the friction force on the block is given by:
W=Ffriction×s
Substituting the expressions for Ffriction and s:
W=μkmg×(12a2t2)
Substituting a2 into the equation:
W=μkmg×(12(μkg−am)t2)
Step 6: Simplify the expression for work done
After simplifying, we get:
W=12μkgt2(μkg−a)
Final Expression
Thus, the work done by friction on the block during time t is:
W=12μkmgt2
The block experiences a kinetic friction force when it slides over the surface. The frictional force can be expressed as:
Ffriction=μkmg
where μk is the coefficient of kinetic friction, m is the mass of the block, and g is the acceleration due to gravity.
The net force acting on the block can be expressed as:
Fnet=Ffriction−Fapplied=μkmg−ma
where a is the acceleration of the block relative to the ground. Rearranging gives:
μkmg=ma+ma1
where a1 is the acceleration of the block with respect to the plank.
From the previous equation, we can express the acceleration a2 (the net acceleration of the block with respect to the ground) as:
a2=μkg−am
The displacement s of the block during time t can be calculated using the formula for displacement under uniform acceleration:
s=12a2t2
The work done W by the friction force on the block is given by:
W=Ffriction×s
Substituting the expressions for Ffriction and s:
W=μkmg×(12a2t2)
Substituting a2 into the equation:
W=μkmg×(12(μkg−am)t2)
After simplifying, we get:
W=12μkgt2(μkg−a)
Thus, the work done by friction on the block during time t is:
W=12μkmgt2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Work done by frictional force
View SolutionWork done by a frictional force is
View SolutionWork done by a frictional force is
View SolutionThe work done by kinetic friction on a body :
View SolutionWork done by friction in case of pure rolling
View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?
View SolutionWork done by static friction on an object :
View SolutionFind the net work done during the cycle abc.
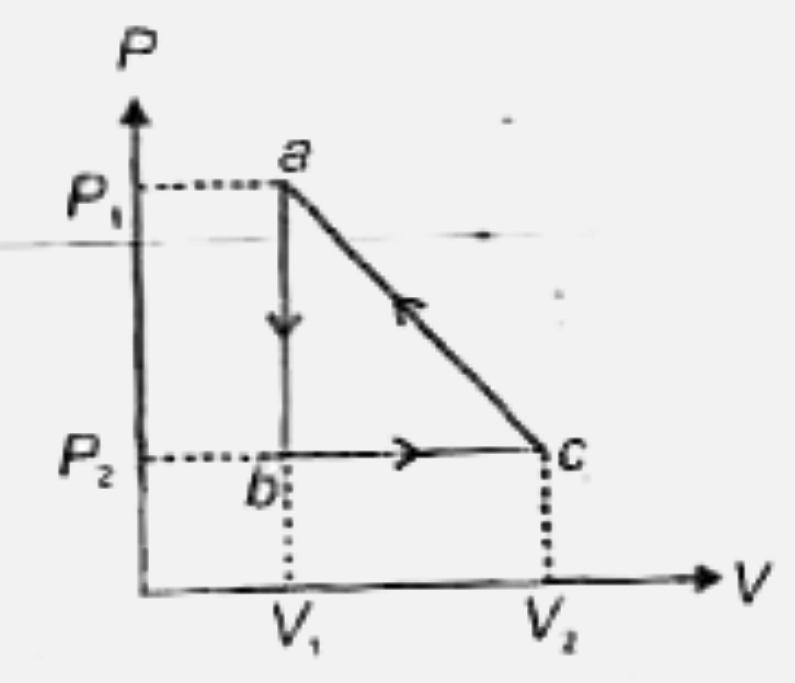
View SolutionA block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
View SolutionA block of mass m is placed on the block of mass M as shown in figure. The horizontal force →F acts on M during time interval t. If the horizontal surface is smooth, assuming no relative sliding between the blocks, find the
a. work done by friction on the blocks
b. work done by →F on the lower block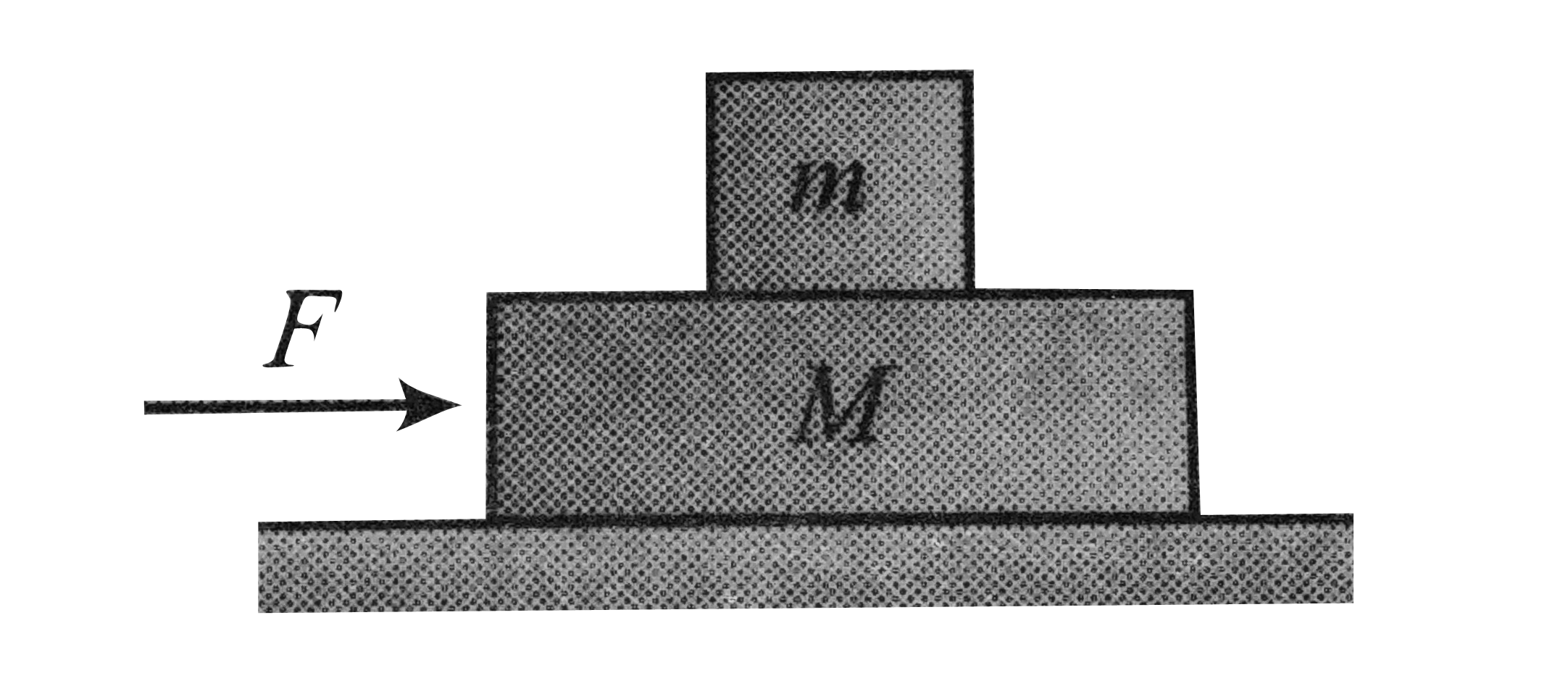
View Solution
