In the proscess T∝ W, pressure of the gas increase from po to to Match the columns.
ColumnIColumnII(A)Temperature of teh gas(p)Pssitive(B)Volume of the gas(q)Nagative(C)work done by the gas(r)Two times(D)Heat supplies to the gas(s)Cannot say anything
The correct Answer is:(A→q,B→t,C→s,D→t)
T∝TVorT∝1T/porT∝√P
p has become four times. Therefore. T has becomes two times or V will have become 12 times.
Since V is decreasing, work done by the gas is negative. Further. T is increasing, hence ΔU will be connot say abour ΔQ. negative and ΔU is positive Hence, ew cannot say about ΔQ
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions14videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective8videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective9videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
Similar Questions
ColumnIColumnII(A)Gas A is ... and gas B is ...(p)Monoatomic, diatomic(B)pA/pBis(q)Diatomic, monoatomic(C)nA/nBis(r)>1(s)<1(t)cannot say anything
View SolutionFor a monotomic gas at temperature T, match the following columns.
ColumnIColumnII(A)Speed of sound(p)√2RT/M(B)RMS speed of gas molecules(q)√8RT/πM(C)Average speed of gas molecules(r)√3RT/M(D)Most probable speed of gas molecules(s)√5RT/3MView SolutionThe straight lines in the figure depict the variations in temperature ΔT as a function of the amount of heat supplied Q is different process involving the change of state of a monoatomic and a diatomic ideal gas . The initial states, (P,V,T) of the two gases are the same . Match the processes as described, with the straight lines in the graph as numbered.
_E01_155_Q01.png)
Column-IColumn-II(A)Isobaric process of monoatomic gas.(p)1(B)Isobaric process of diatomic gas(q)2(C)Isochoric process of monoatomic gas(r)Minimum at section B(D)Isochoric process of diatomic gas(s)x-axis (i.e.'Q' axis)View SolutionIn a process V∝T2, temperature of 2 moles of a gas is increased by 200K. Work done by the gas in this process will be
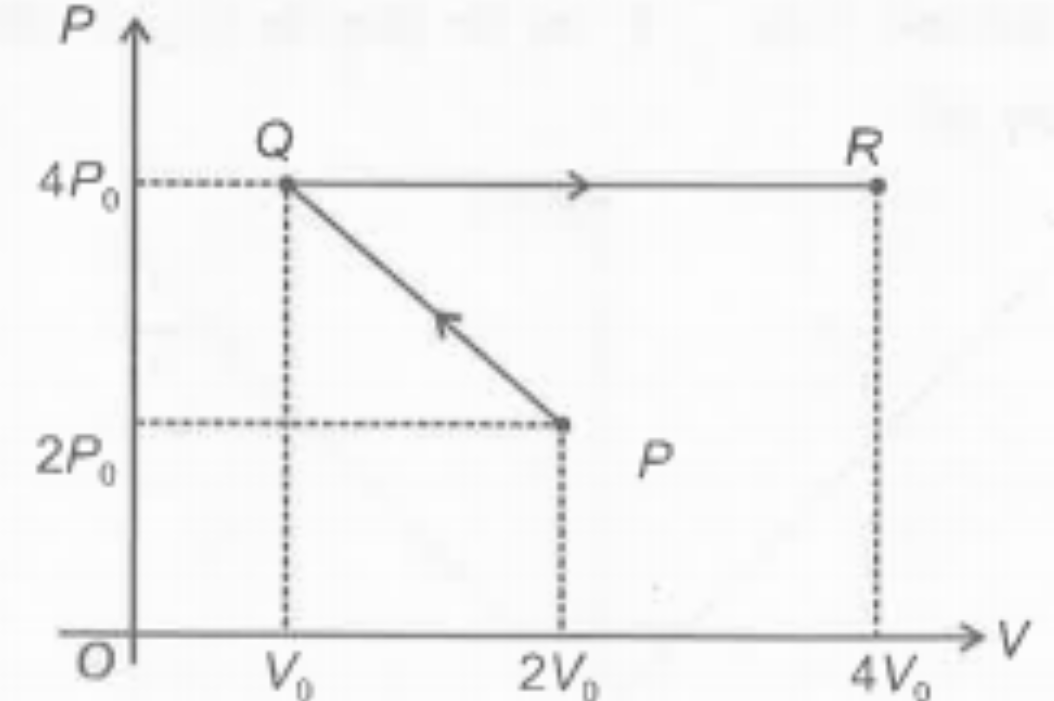
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
View SolutionThe volume of a monatomic ideal gas increases linearly with pressure, as shown in Fig. Calculate (a) increase in internal energy, (b) work done by the gas and (c ) heat supplied to the gas.
View SolutionOne mole of a gas is enclosed in a cylinde in a cyclinder and occupies a volume of 1.5L at a pressure 1.5 atm. It is subjected to strong heating due to which temperature of the gas increase according to the relation T=αV2, where α is a positive constant and V is volume of the gas.
a. Find the work done by air in increasing the volume of gas to 9L.
b. Draw the P−V diagram of the process.
c. Determine the heat supplied to the gas (assuming γ=1.5).View SolutionThree moles of an ideal gas at a pressure PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original , volume. Finally the gas is compressed at constant volume to its original pressure PA
(a) Sketch the P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.View SolutionA monoatomic gas at a temperature T has pressure P and heat energy per unit volume E. then
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
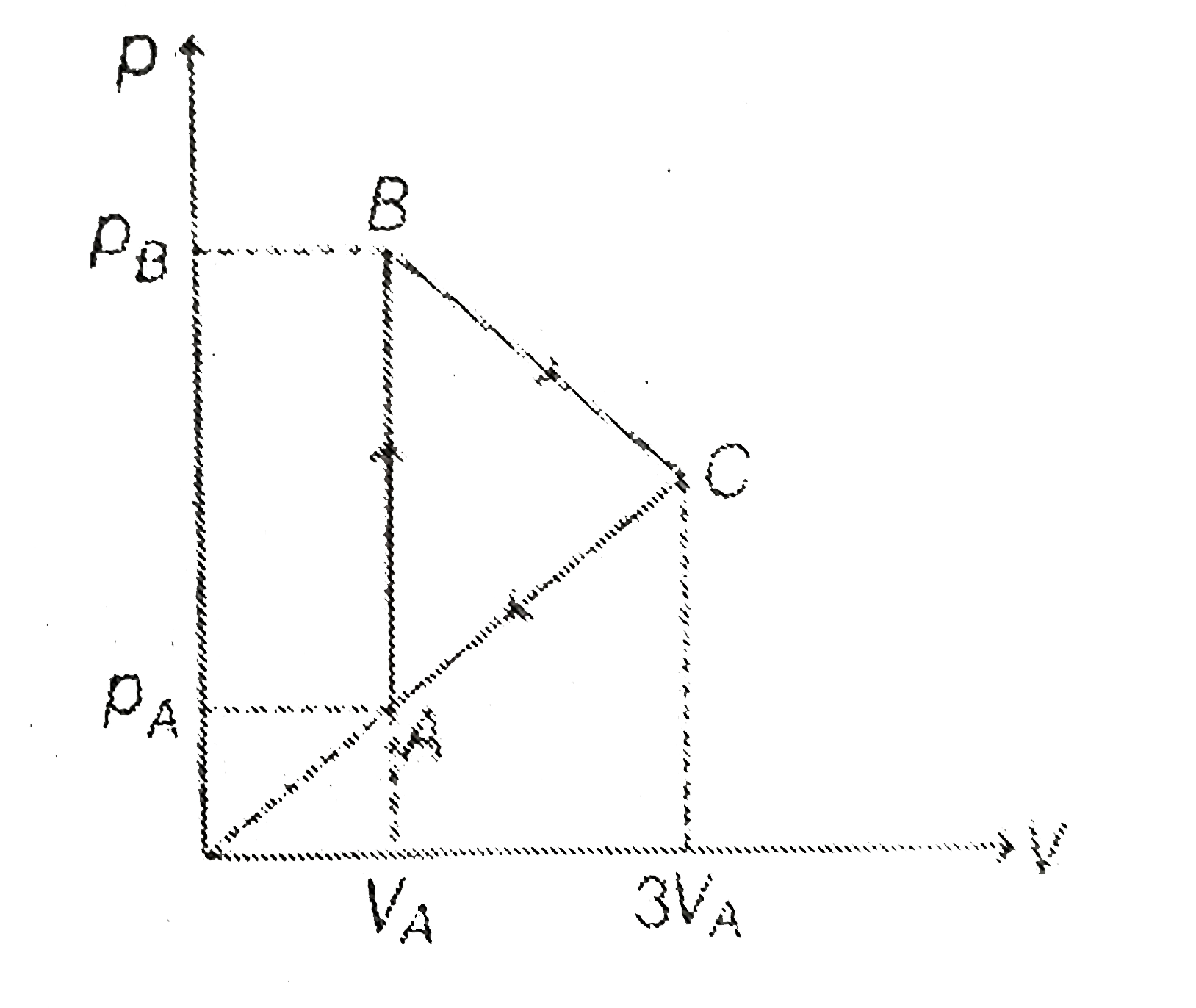
Net work done by the gas in the process isView Solution