In the question number 62, the distance from the thrower to the point where the ball returns to the same level is
58 m
68 m
78 m
88 m
The correct Answer is:C
To solve the problem of finding the distance from the thrower to the point where the ball returns to the same level, we will use the formula for the range of a projectile. Here are the steps:
1. Identify the given values:
- Initial velocity (u) = 30 m/s
- Angle of projection (θ) = 30 degrees
- Acceleration due to gravity (g) = 10 m/s²
2. Use the range formula for projectile motion:
The range (R) of a projectile is given by the formula:
R=u2sin(2θ)g
3. Calculate sin(2θ):
- First, calculate 2θ:
2θ=2×30∘=60∘
- Now, find sin(60∘):
sin(60∘)=√32
4. Substitute the values into the range formula:
R=(30m/s)2⋅sin(60∘)10m/s2
R=900⋅√3210
5. Simplify the expression:
R=900⋅√3210=900√320=45√3
6. Calculate the numerical value:
- Using √3≈1.732:
R≈45×1.732≈77.94m
7. Round to the nearest whole number:
R≈78m
Final Answer:
The distance from the thrower to the point where the ball returns to the same level is approximately 78 meters.
- Initial velocity (u) = 30 m/s
- Angle of projection (θ) = 30 degrees
- Acceleration due to gravity (g) = 10 m/s²
The range (R) of a projectile is given by the formula:
R=u2sin(2θ)g
- First, calculate 2θ:
2θ=2×30∘=60∘
- Now, find sin(60∘):
sin(60∘)=√32
R=(30m/s)2⋅sin(60∘)10m/s2
R=900⋅√3210
R=900⋅√3210=900√320=45√3
- Using √3≈1.732:
R≈45×1.732≈77.94m
R≈78m
The distance from the thrower to the point where the ball returns to the same level is approximately 78 meters.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS
9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
A cricket ball is thrown at a speed of 28ms−1 in a direction 30∘ above the horizontal. Calculate (a)the maximum height (b) the time taken by ball to return to the same level, and (c )the distance from the thrower to the point where the ball returns to the same level.
View SolutionA ball is throw from the top of a tower of 61 m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizon. What is the distance from the foot of the tower to the point where the ball hits the ground ?
View Solution
Knowledge Check
In the question number 62, the linear acceleration of the rope is
A5ms−2B10ms−2C15ms−2D20ms−2In the question number 62. the maximum height attained by the ball is
A11.25 mB48.2 mC23. 5 mD68 mIn the question number 56, the maximum horizontal distance covered by the ball will be
A160√3 mB140√3 mC120√3 mD100√3 m
A ball is thrown with the velocity u at an angle of α to the horizon. Find (i) the height of which the ball will rise to (ii) the distance x from the point of projection to the point where it reaches to the ground and (iii) the time during which the ball will be in motion (neglect the air resistance ).
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

View SolutionA cylindrical hall has a horizontal smooth floor. A ball is projected along the floor from A point on the wall in a direction making an angle θ with the radius through the point the ball returns bak to the initial point after two impacts with the wall. if the coefficient of restitution is e than tan2θ will be
View SolutionA ball swings back and forth in front of a concave mirror. The motion of the ball is described approximately by the equation x=fcos(ω)t, where f is the focal length of the mirror and x is measured along the axis of mirror. The origin is taken at the centre of curvature of the mirror.
(a) Derive an expression for the distance from the mirror of the image of the swinging ball.
(b) At what point does the ball appear to coincide with its image?
(c) What will be the lateral magnifiaction of the image of the ball at time t=T2, where T is time period of oscillation?
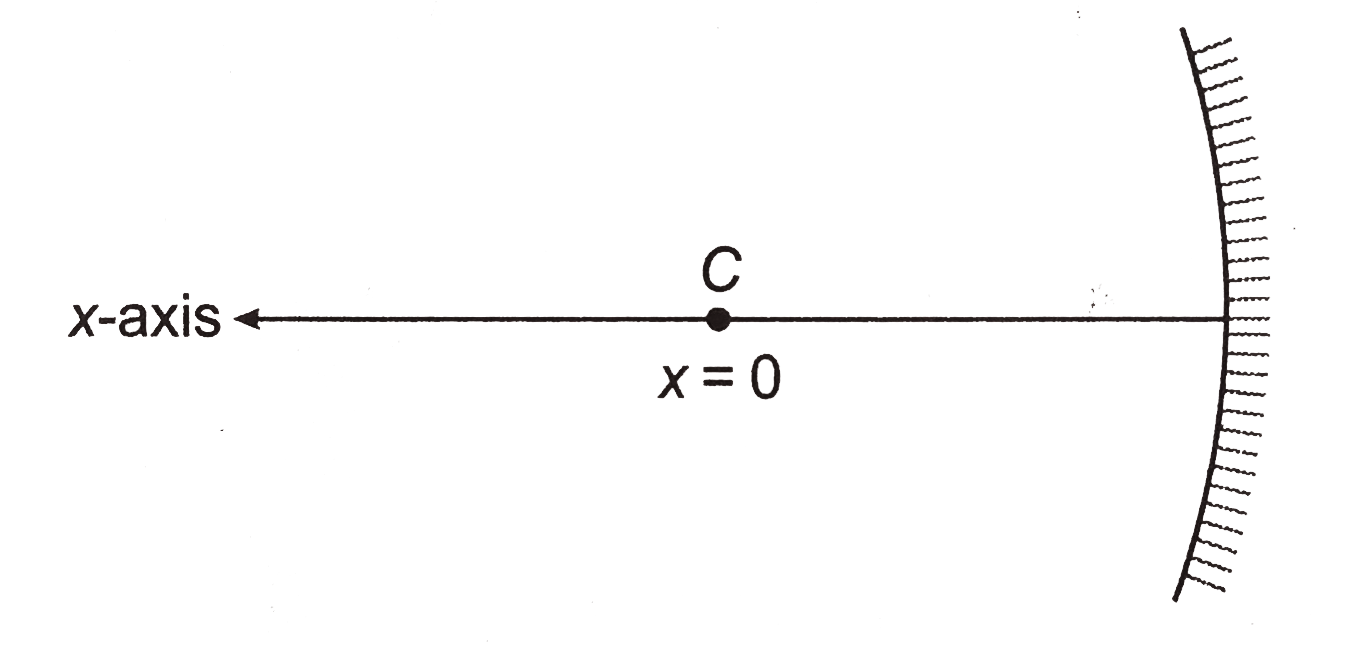
View SolutionA cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
View Solution
