In the regular hexagon shown in Fig. 3.51, →AB+→BC+→CD+→DE+→EF+→AF can be expressed as :
−2→FA
zero
2→FA
→FA
The correct Answer is:A
Step by step video, text & image solution for In the regular hexagon shown in Fig. 3.51, vecAB + vecBC + vecCD+ vecDE + vecEF+ vecAF can be expressed as : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - MORE THAN ONE CHOICE IS CORRECT15videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - ASSERTION- REASON1videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - PROBLEMS FOR PARCTICE23videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression6videos
UNITS AND DIMENSIONS
Similar Questions
.Knowledge Check
- Question 1 - Select One
In the regular hexagon shown in fig.3.51, →AO+→BO+→CO+→DO+→EO+→FO can be expressed as :
AzeroB−2→OCC−2→OFD→OF - Question 2 - Select One
In a regular hexagon ABCDEF,
→AB+→AC+→AD+→AE+→AF=A4→ADB3→ADC2→ADD0 - Question 3 - Select One
Let ABCDEF be a regular hexagon. If →AD=x→BC and →CF=y→AB, then xy =
A−4B−2C2D4
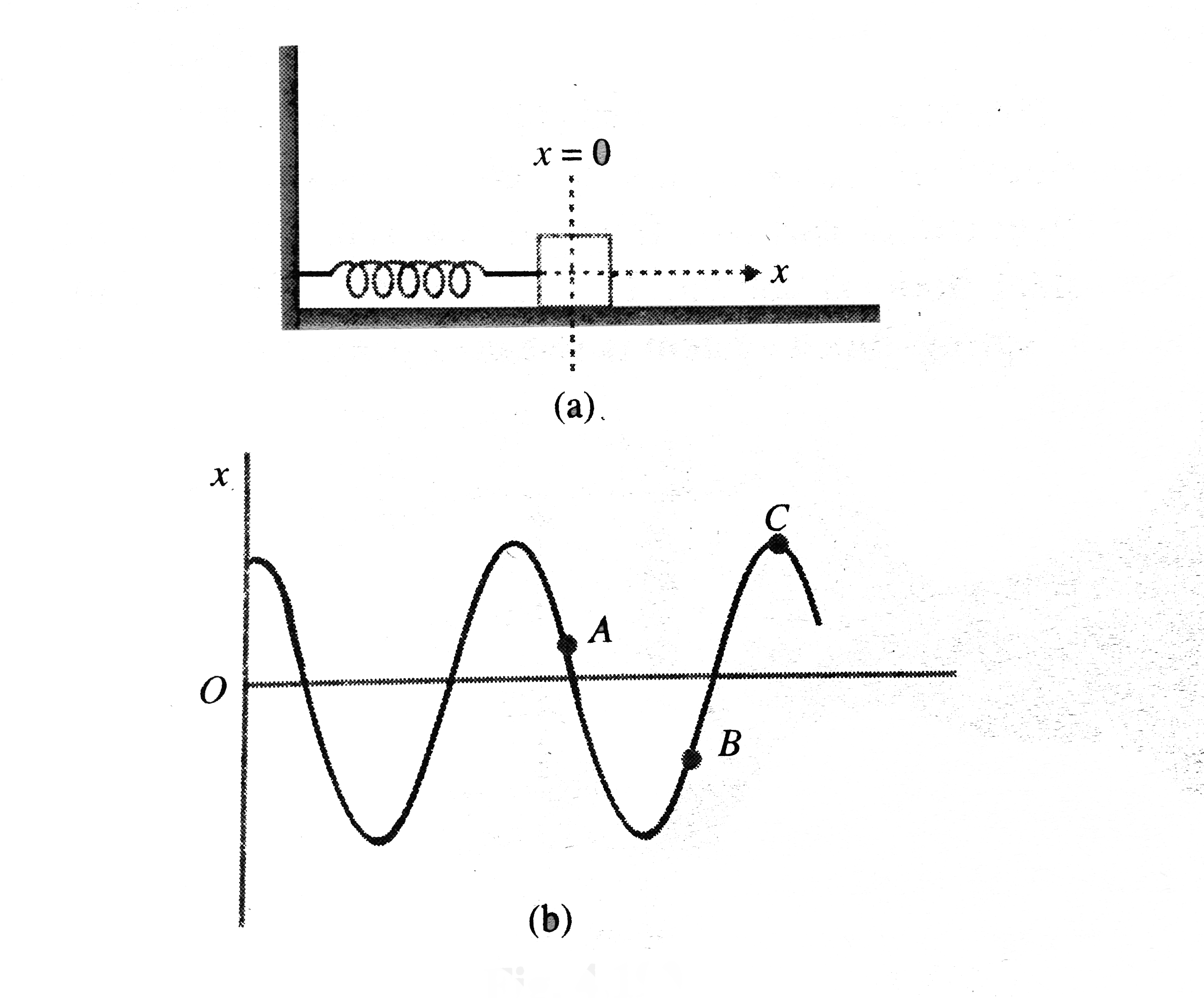
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed asView Solution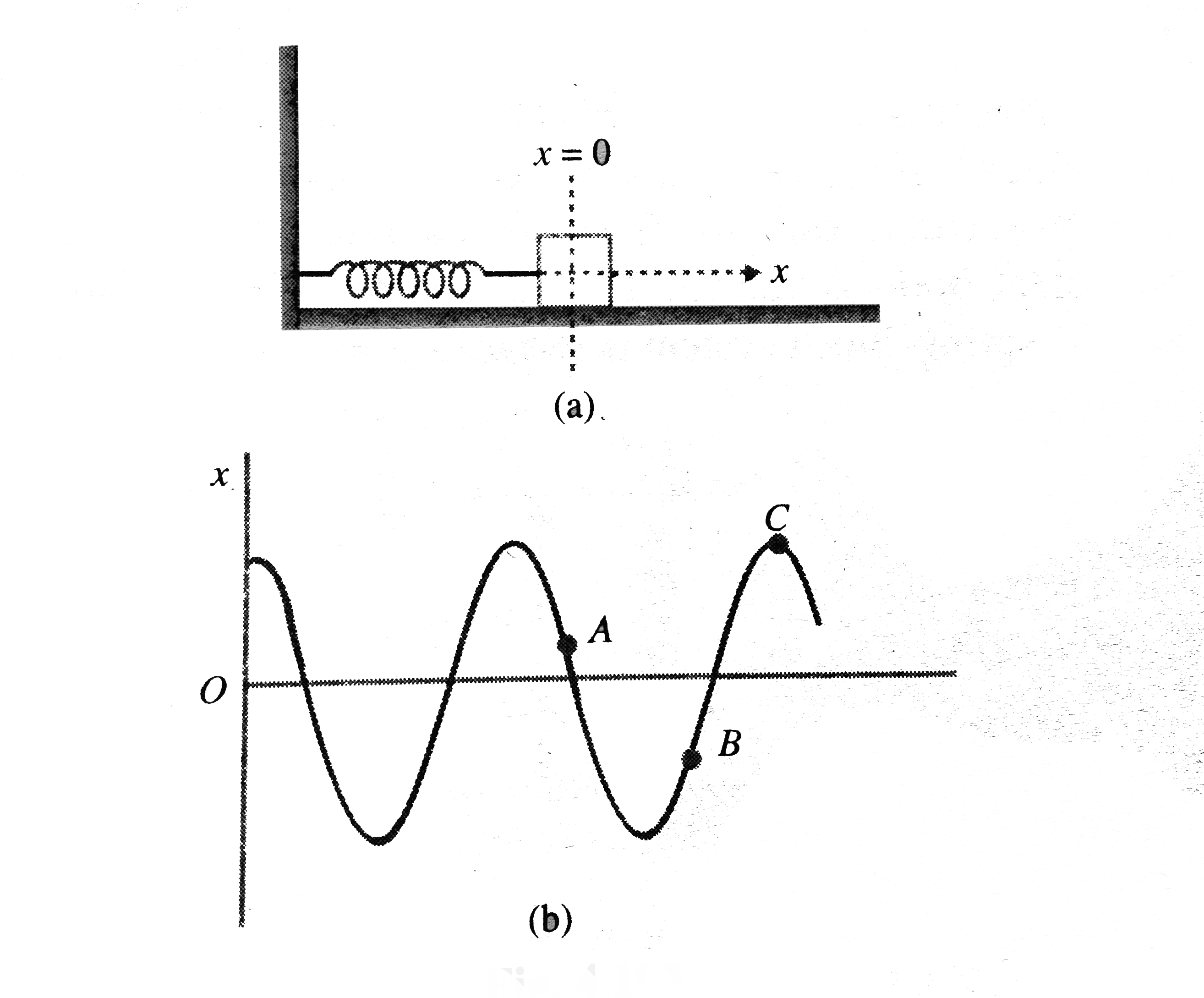
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
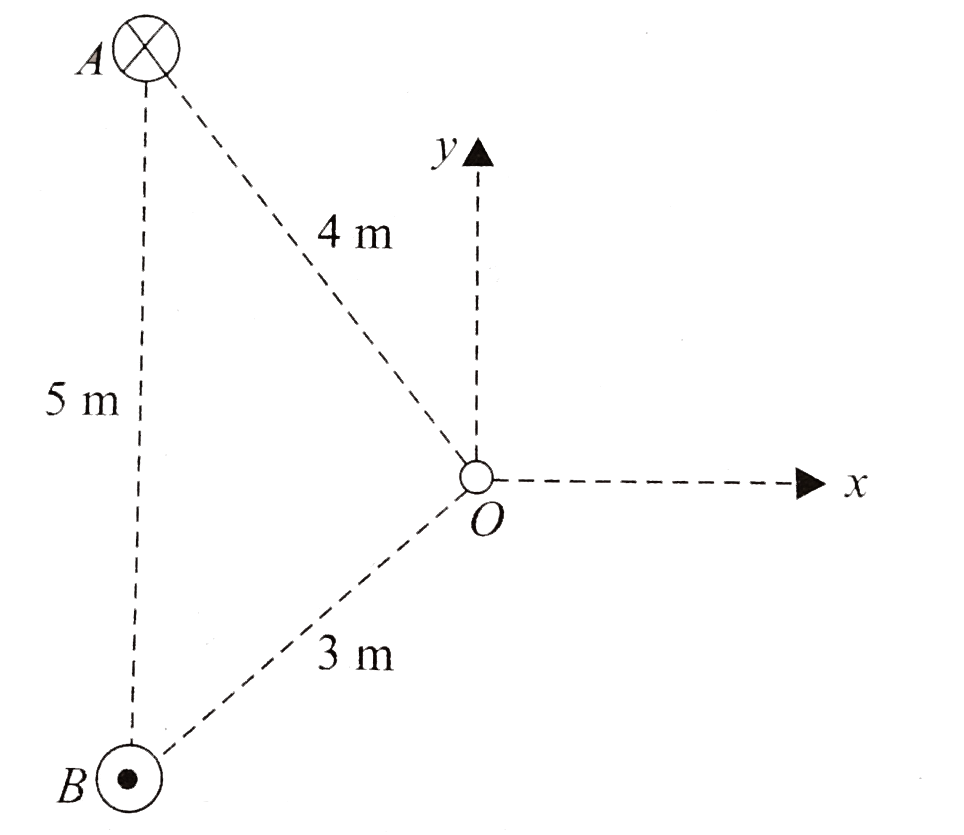
Position of the block as a function of time can now be expressed asView SolutionTwo infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
View SolutionA small metal sphere, carrying a net charge q1=−2μC, is held in a stationary position by insulating supports. A second small metal sphere, with a net charge of q2=−8μC and mass 1.50g, is projected toward q1. When the two spheres are 0.800m apart, q2 is moving toward q1 with speed 20ms−1 as shown in (Fig. 3.151). Assume that the two spheres can be treated as point charges. You can ignore the force of gravity.
.
How close does q2 get to q1 ?View SolutionA small metal sphere, carrying a net charge q1=−2μC, is held in a stationary position by insulating supports. A second small metal sphere, with a net charge of q2=−8μC and mass 1.50g, is projected toward q1. When the two spheres are 0.800m apart, q2 is moving toward q1 with speed 20ms−1 as shown in (Fig. 3.151). Assume that the two spheres can be treated as point charges. You can ignore the force of gravity.
.
The speed of q2 when the spheres are 0.400m apart is.View Solution