In the regular hexagon shown in fig.3.51, →AO+→BO+→CO+→DO+→EO+→FO can be expressed as :
zero
−2→OC
−2→OF
→OF
The correct Answer is:B
Topper's Solved these Questions
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - MORE THAN ONE CHOICE IS CORRECT
15 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - ASSERTION- REASON
1 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - PROBLEMS FOR PARCTICE
23 Videos
- UNITS AND DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression
6 Videos
Similar Questions
In the regular hexagon shown in figure −−→AB+−−→BC+−−→CD+−−→DE+−−→EF+−−→AF can be expressed as :
View Solution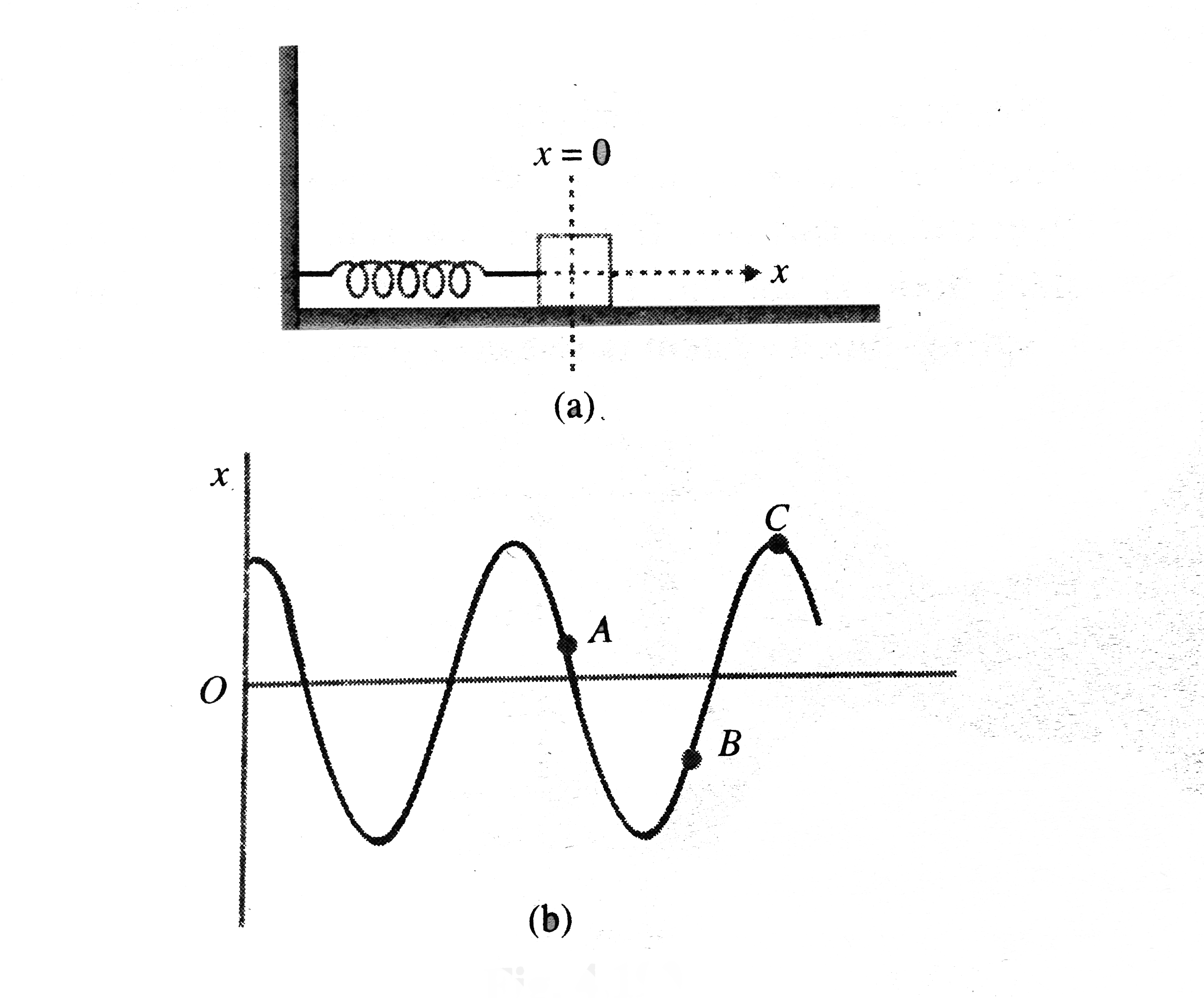
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
View Solution
Knowledge Check
In the regular hexagon shown in Fig. 3.51, →AB+→BC+→CD+→DE+→EF+→AF can be expressed as :
A−2→FABzeroC2→FAD→FA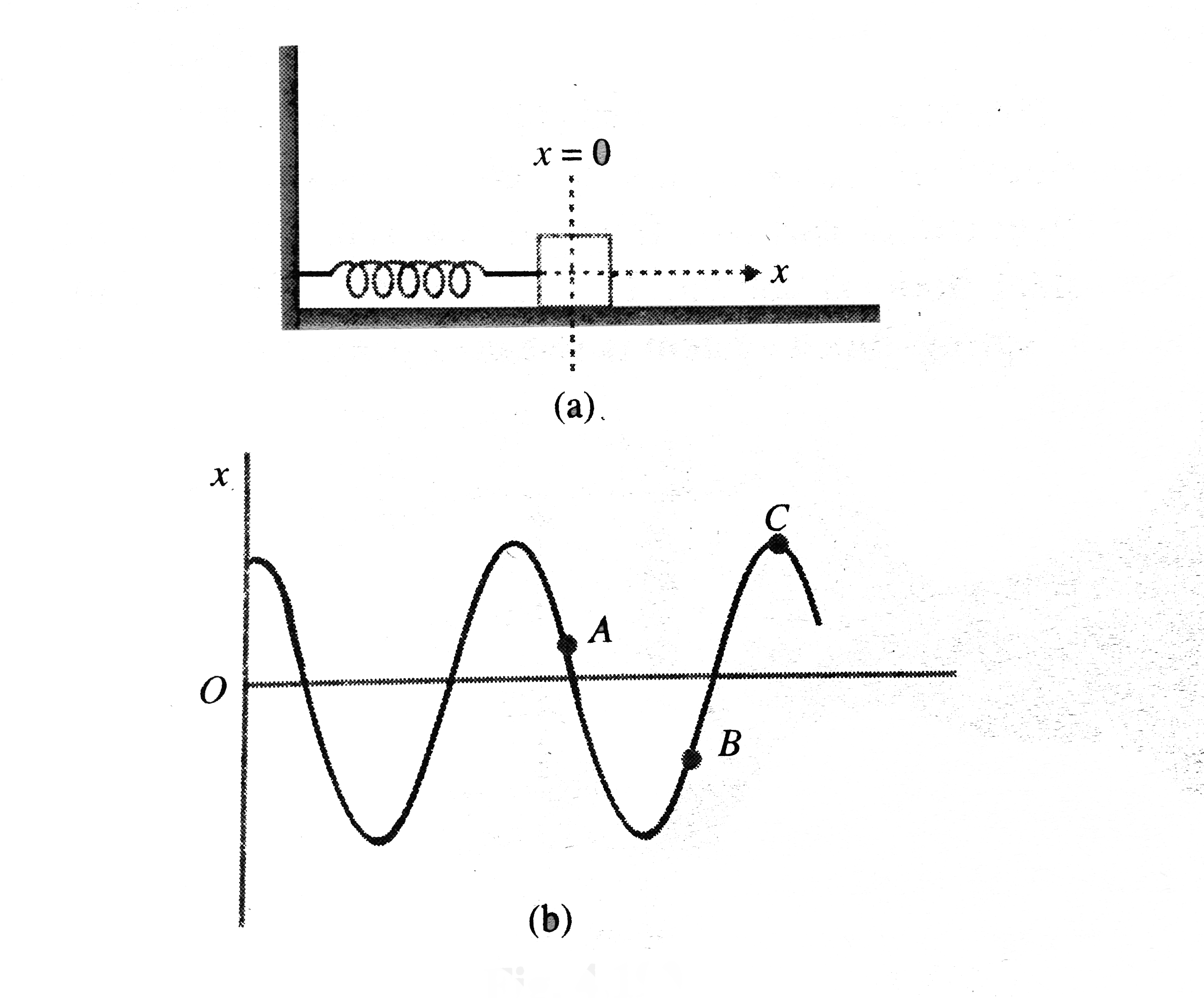
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed asAv=−sin48(16tπ2)cmsBv=−48sin(16tπ3)cmsCv=−56sin(16tπ4)cmsDv=−56(16tπ6)cms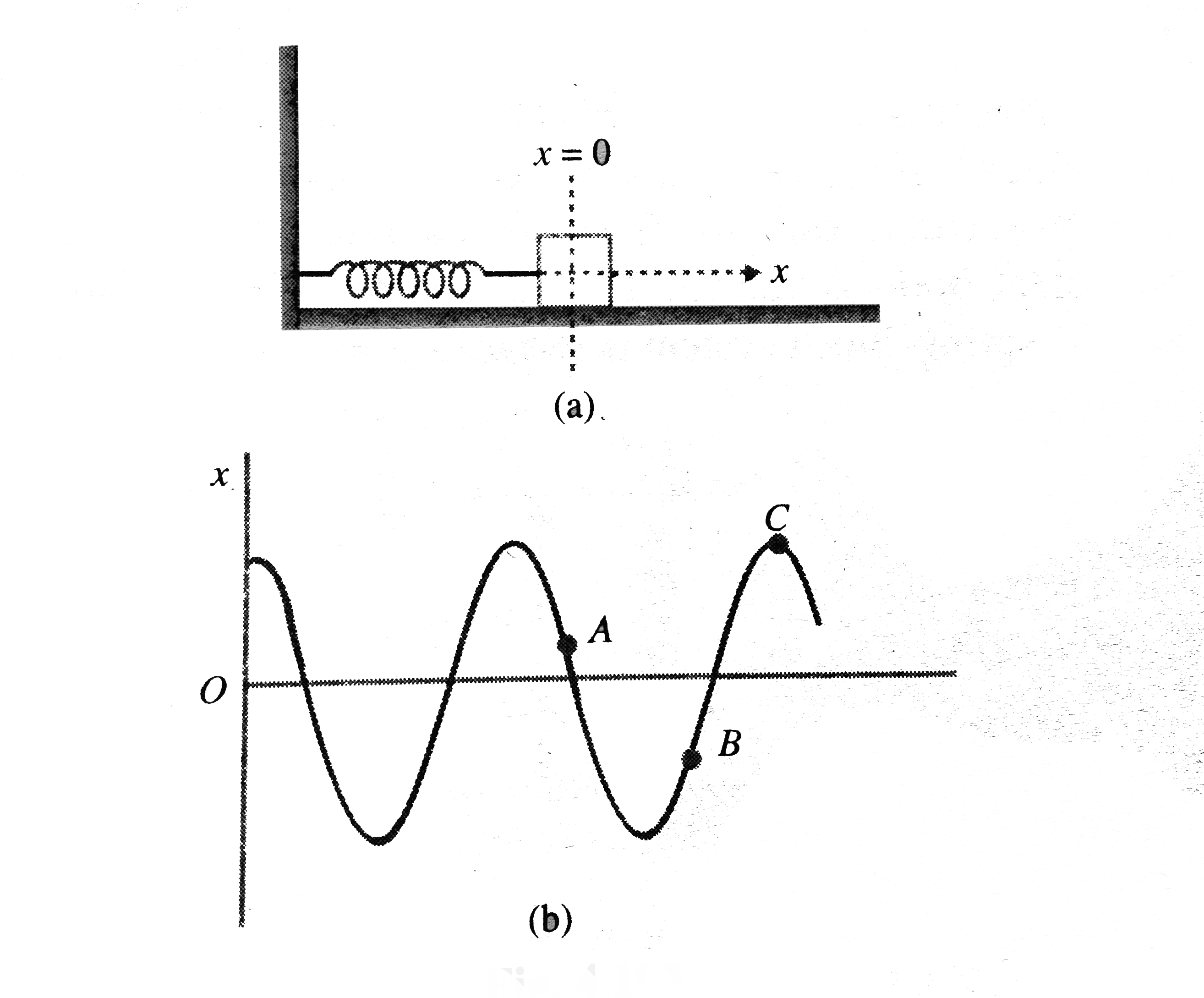
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Position of the block as a function of time can now be expressed asAx=3cos(16t+π2)cmBx=3cos(16t+π3)cmCx=3.5cos(16t+π6)cmDx=3.2cos(16t+π4)cm
In the circuit shown in (fig. 3.51), find the current recorded by ammeter (A).
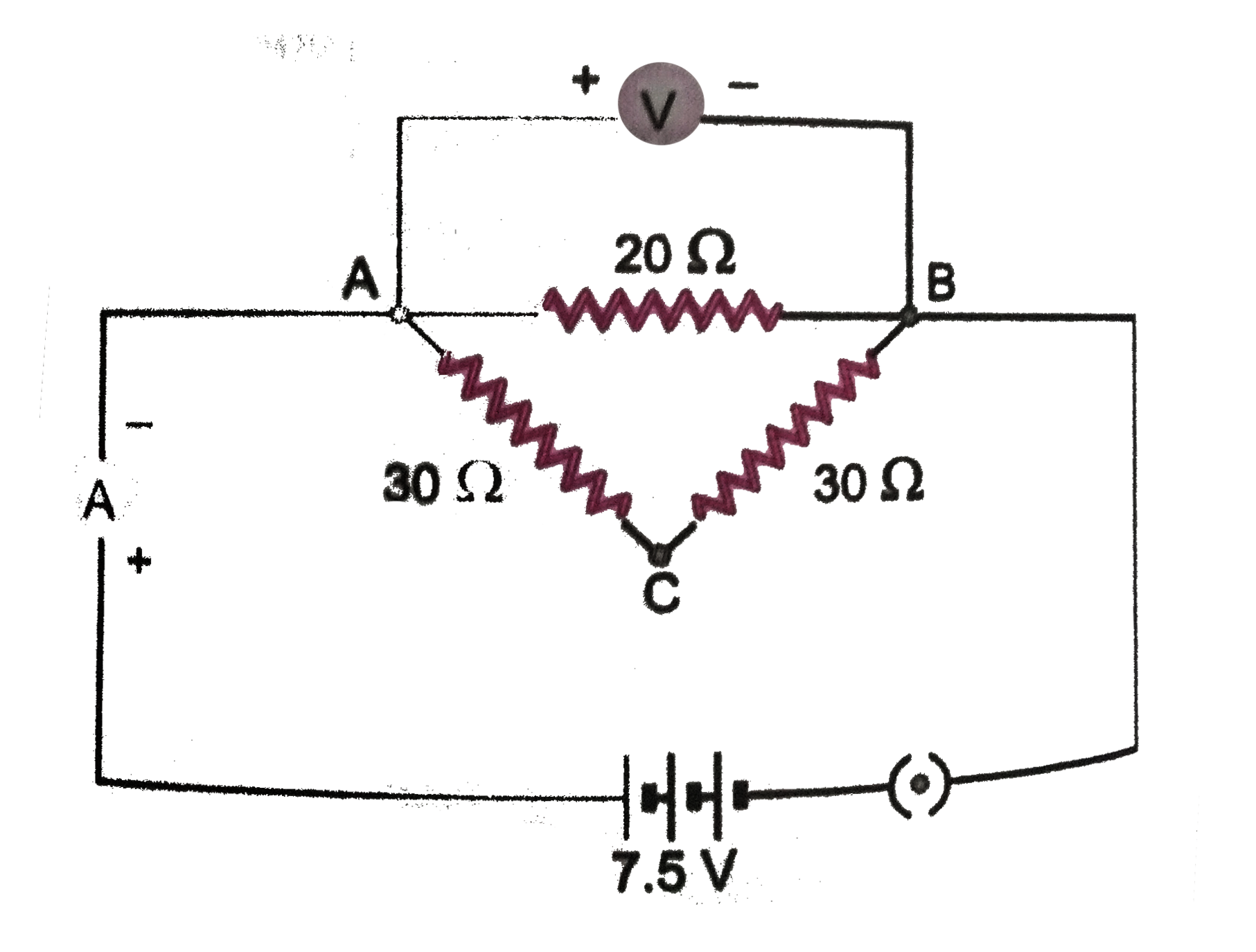 .
.
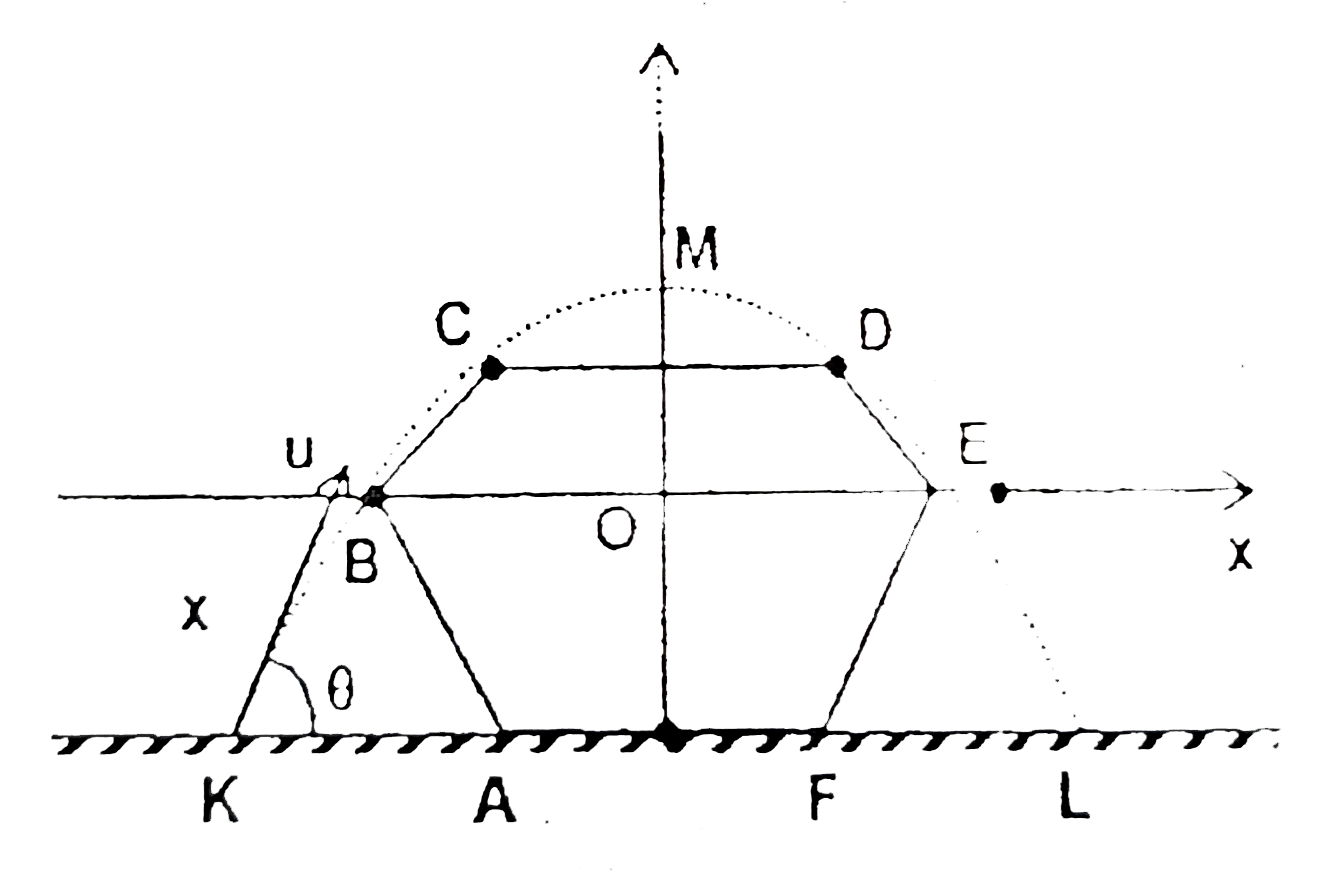
View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The maximum height from horizontal surface attained by projectile is

View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The time required to move the particle from D to E is
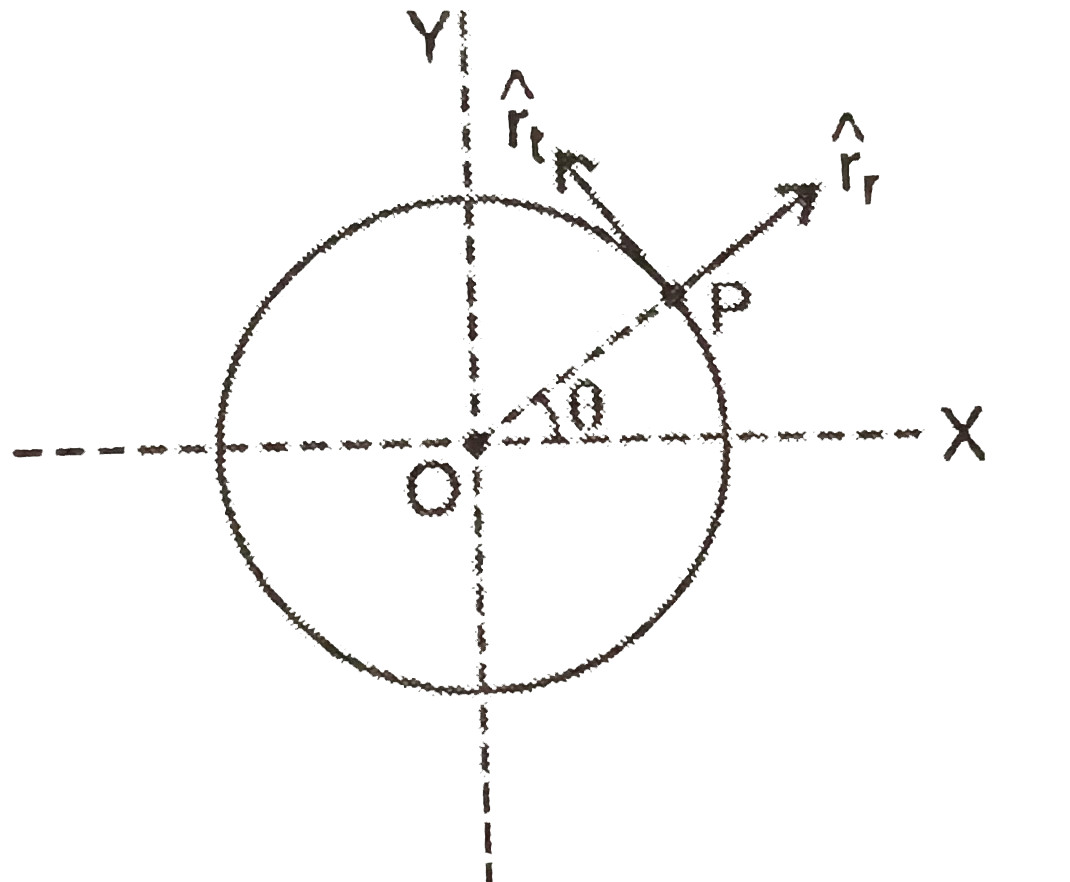
View SolutionConsider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
Answer the following questions :
For any position of the objected P, the tangential unit vector can be expressed as :
View SolutionAn oscillator of frequency 680Hz drives two speakers . The speakers are fixed on a vertical pole at a distance 3m from each other as shown in Fig. 7.103. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that there is no reflection of sound from the ground and speed of sound is v=340m/s , answer the following questions.

At some instant , when the person is at a distance 4m from the pole , the wave function ( at the person's location) that describes the waves coming from the lower speaker y=Acos(kx−ωt) , where A is the amplitude , ω=2πv with v=680Hz (given) and k=2π/λ
Wave function ( at the person's location) that describes waves coming from the upper speaker can be expressed as :
View Solution
