In the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

The maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)
The maximum possible speed of the blocks is g(μm1)√k(m1+m2)
The maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)
The maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
The correct Answer is:A, C
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions18videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions10videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct42videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
Two blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
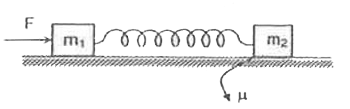 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Block A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-
 Am/2Bm/3C2m/3Dm/√3
Am/2Bm/3C2m/3Dm/√3 - Question 2 - Select One
Consider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
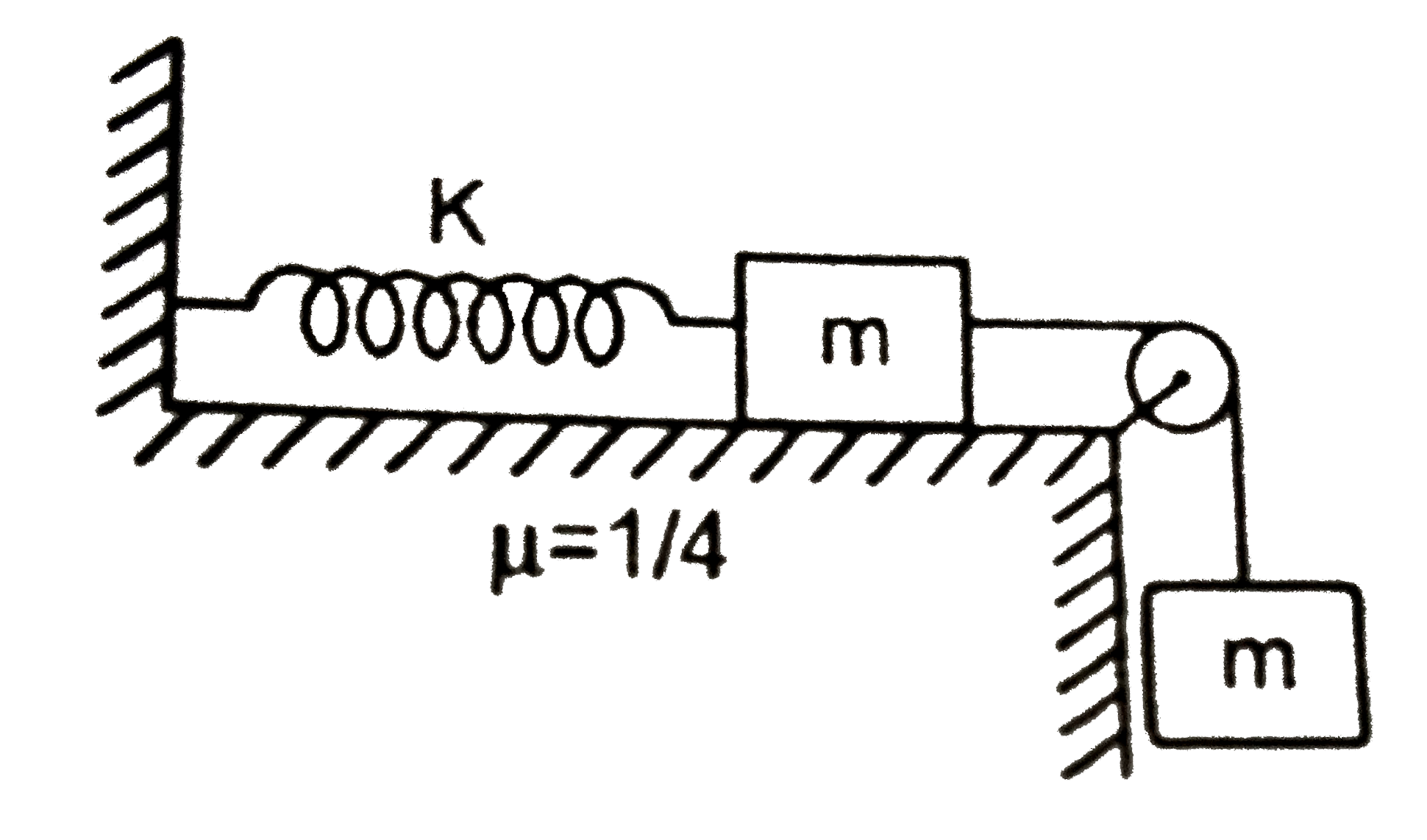
If the string connecting both the masses is cut just at the instant both masses came to momentary rest for the first time in question 5, then maximum compression of spring during resulting motion is (Take μ=1/4)A2mg3KBmg2KCmgKD1mg3K - Question 3 - Select One
Two blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)g
Two blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
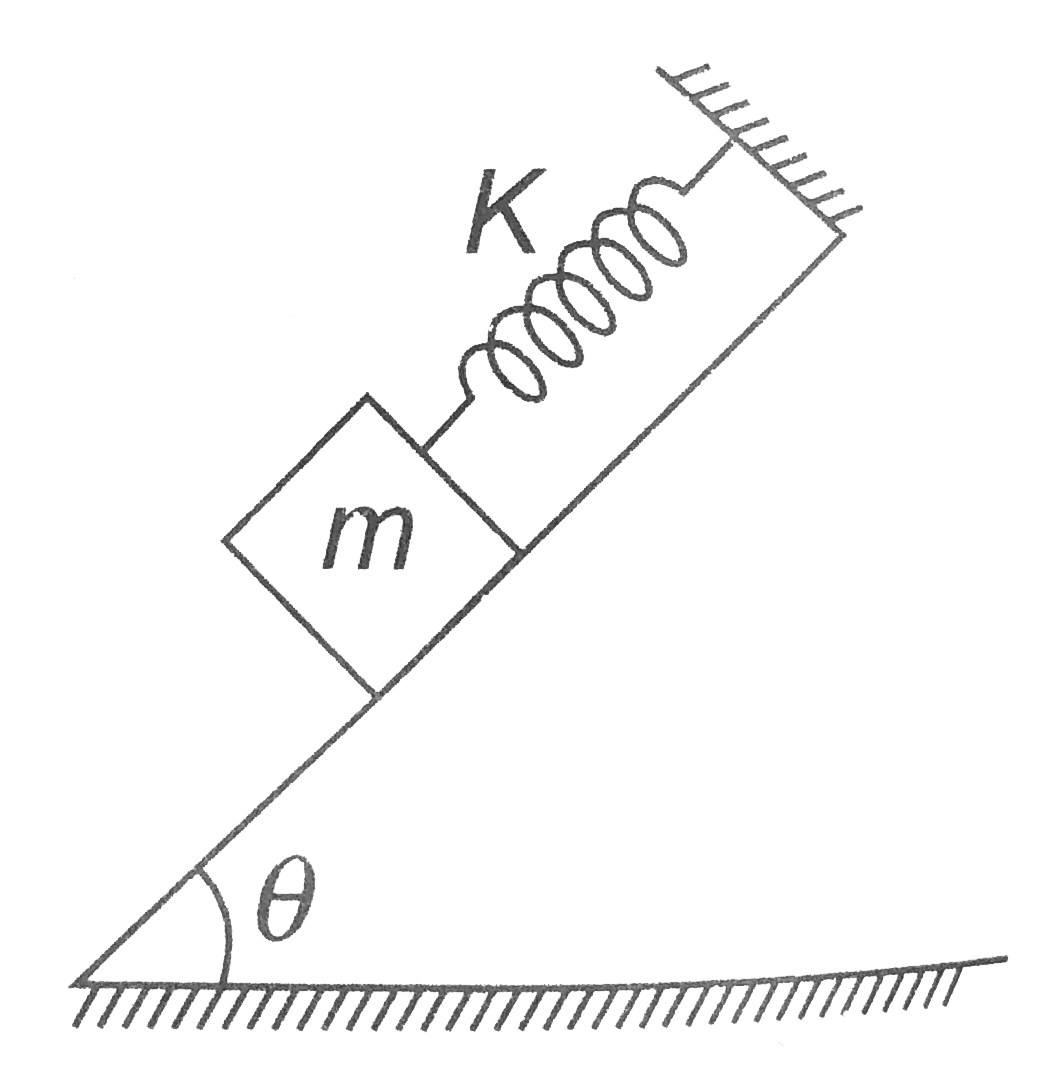 View Solution
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
 View Solution
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution

