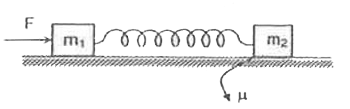
Two block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
8 N
15 N
10 N
25 N
The correct Answer is:A
To solve the problem of determining the minimum constant force F that must be applied to block m1 in order to shift block m2, we can follow these steps:
1. Understanding the Forces:
- Block m1 is connected to block m2 by a light spring. The coefficient of friction between both blocks and the surface is μ.
- The force F is applied to block m1 in the horizontal direction.
2. Identifying the Condition for Block m2 to Move:
- For block m2 to start moving, the force exerted by the spring on block m2 (let's denote it as kx, where k is the spring constant and x is the extension of the spring) must overcome the frictional force acting on block m2.
- The limiting frictional force ffriction on block m2 is given by:
ffriction=μm2g
3. Setting Up the Equation:
- For block m2 to start moving, we need:
kx≥μm2g
4. Applying Work-Energy Principle:
- The work done by the applied force F must equal the work done against friction and the work done on the spring. The work-energy theorem states:
F⋅x=ffriction⋅x+12kx2
- Substituting ffriction:
F⋅x=μm2g⋅x+12kx2
5. Simplifying the Equation:
- Dividing through by x (assuming x≠0):
F=μm2g+12kx
6. Finding Minimum Force F:
- To find the minimum force F, we need to minimize the term kx. The minimum value of kx occurs when kx=μm2g (from step 3).
- Substituting this back into the equation for F:
Fmin=μm2g+12μm2g=32μm2g
7. Final Expression:
- Therefore, the minimum constant force F that must be applied to block m1 to shift block m2 is:
Fmin=μ(m1+m2)g
- Block m1 is connected to block m2 by a light spring. The coefficient of friction between both blocks and the surface is μ.
- The force F is applied to block m1 in the horizontal direction.
- For block m2 to start moving, the force exerted by the spring on block m2 (let's denote it as kx, where k is the spring constant and x is the extension of the spring) must overcome the frictional force acting on block m2.
- The limiting frictional force ffriction on block m2 is given by:
ffriction=μm2g
- For block m2 to start moving, we need:
kx≥μm2g
- The work done by the applied force F must equal the work done against friction and the work done on the spring. The work-energy theorem states:
F⋅x=ffriction⋅x+12kx2
- Substituting ffriction:
F⋅x=μm2g⋅x+12kx2
- Dividing through by x (assuming x≠0):
F=μm2g+12kx
- To find the minimum force F, we need to minimize the term kx. The minimum value of kx occurs when kx=μm2g (from step 3).
- Substituting this back into the equation for F:
Fmin=μm2g+12μm2g=32μm2g
- Therefore, the minimum constant force F that must be applied to block m1 to shift block m2 is:
Fmin=μ(m1+m2)g
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Two block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mgA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionTwo blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View Solution
