In the system shown in the figure the string, springs and pulley are light. The force constant of the two springs are . Block of mass M is pulled vertically down from its equilibrium position and released. Calculate the angular frequency of oscillation. The top surface of the block (represented by line AB) always remains horizontal.

The correct Answer is:
Step by step video, text & image solution for In the system shown in the figure the string, springs and pulley are light. The force constant of the two springs are k_(1) = k " and " k_(2) = 2k. Block of mass M is pulled vertically down from its equilibrium position and released. Calculate the angular frequency of oscillation. The top surface of the block (represented by line AB) always remains horizontal. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 3
Explore 9 Videos
- SIMPLE HARMONIC MOTIONBook:ARIHANTChapter:SIMPLE HARMONIC MOTIONExercise:Level 3
Explore 9 Videos
- ROTATIONAL MOTIONBook:ARIHANTChapter:ROTATIONAL MOTIONExercise:PHYSICS
Explore 159 Videos
- SURFACE TENSIONBook:ARIHANTChapter:SURFACE TENSIONExercise:Surface tension
Explore 33 Videos
Similar Questions
A system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
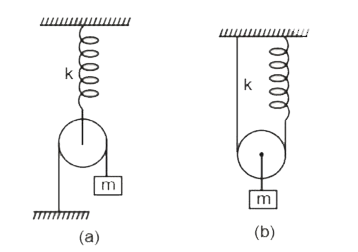
View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKAn elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mkTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
Figure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution