In which of the following cases the havier of the two particles has a smaller de-Broglie wavelength ? The two particles
move with the same speed
move with the same linear momentum
move with the same kinetic energy
have the same change of potential energy in a conservative field
The correct Answer is:A, C
To determine in which of the given cases the heavier of the two particles has a smaller de-Broglie wavelength, we need to analyze the relationship between mass, momentum, and de-Broglie wavelength.
1. Understanding de-Broglie Wavelength:
The de-Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
2. Momentum and Kinetic Energy:
The momentum (p) of a particle can also be expressed in terms of its mass (m) and velocity (v):
p=mv
The kinetic energy (K) of a particle is given by:
K=12mv2
From this, we can express velocity in terms of kinetic energy:
v=√2Km
3. Substituting into de-Broglie Wavelength:
By substituting the expression for momentum in terms of kinetic energy into the de-Broglie wavelength equation, we get:
λ=hmv
Substituting v:
λ=hm√2Km=h√2Km=h√2K⋅1√m
This shows that the de-Broglie wavelength is inversely proportional to the square root of the mass when kinetic energy is constant.
4. Analyzing Each Case:
- Case 1: Both particles moving with the same speed:
- Here, λ is inversely proportional to m. Hence, the heavier particle will have a smaller wavelength.
- Case 2: Both particles have the same momentum:
- If both have the same momentum, they will have the same de-Broglie wavelength. Thus, this case is incorrect.
- Case 3: Both particles have the same kinetic energy:
- From our earlier derivation, if kinetic energy is the same, the heavier particle has a smaller de-Broglie wavelength.
- Case 4: Both particles have the same change in potential energy:
- This does not provide enough information about their initial and final kinetic energies. Thus, we cannot conclude which particle has a smaller wavelength.
5. Conclusion:
The cases where the heavier particle has a smaller de-Broglie wavelength are:
- Case 1: Both particles moving with the same speed.
- Case 3: Both particles have the same kinetic energy.
Final Answer:
The heavier of the two particles has a smaller de-Broglie wavelength in cases 1 and 3.
---
The de-Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
The momentum (p) of a particle can also be expressed in terms of its mass (m) and velocity (v):
p=mv
The kinetic energy (K) of a particle is given by:
K=12mv2
From this, we can express velocity in terms of kinetic energy:
v=√2Km
By substituting the expression for momentum in terms of kinetic energy into the de-Broglie wavelength equation, we get:
λ=hmv
Substituting v:
λ=hm√2Km=h√2Km=h√2K⋅1√m
This shows that the de-Broglie wavelength is inversely proportional to the square root of the mass when kinetic energy is constant.
- Case 1: Both particles moving with the same speed:
- Here, λ is inversely proportional to m. Hence, the heavier particle will have a smaller wavelength.
- Case 2: Both particles have the same momentum:
- If both have the same momentum, they will have the same de-Broglie wavelength. Thus, this case is incorrect.
- Case 3: Both particles have the same kinetic energy:
- From our earlier derivation, if kinetic energy is the same, the heavier particle has a smaller de-Broglie wavelength.
- Case 4: Both particles have the same change in potential energy:
- This does not provide enough information about their initial and final kinetic energies. Thus, we cannot conclude which particle has a smaller wavelength.
The cases where the heavier particle has a smaller de-Broglie wavelength are:
- Case 1: Both particles moving with the same speed.
- Case 3: Both particles have the same kinetic energy.
The heavier of the two particles has a smaller de-Broglie wavelength in cases 1 and 3.
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Comprehension Based
3 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2Passage 2
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Single Correct
22 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Knowledge Check
Which of these particles having the same kinetic energy has the largest de Broglie wavelength ?
AElectronBAlpha particleCProtonDNeutronWhich of the following figure represents the variation of particle momentum and the associated de - Broglie wavelength ?
A B
B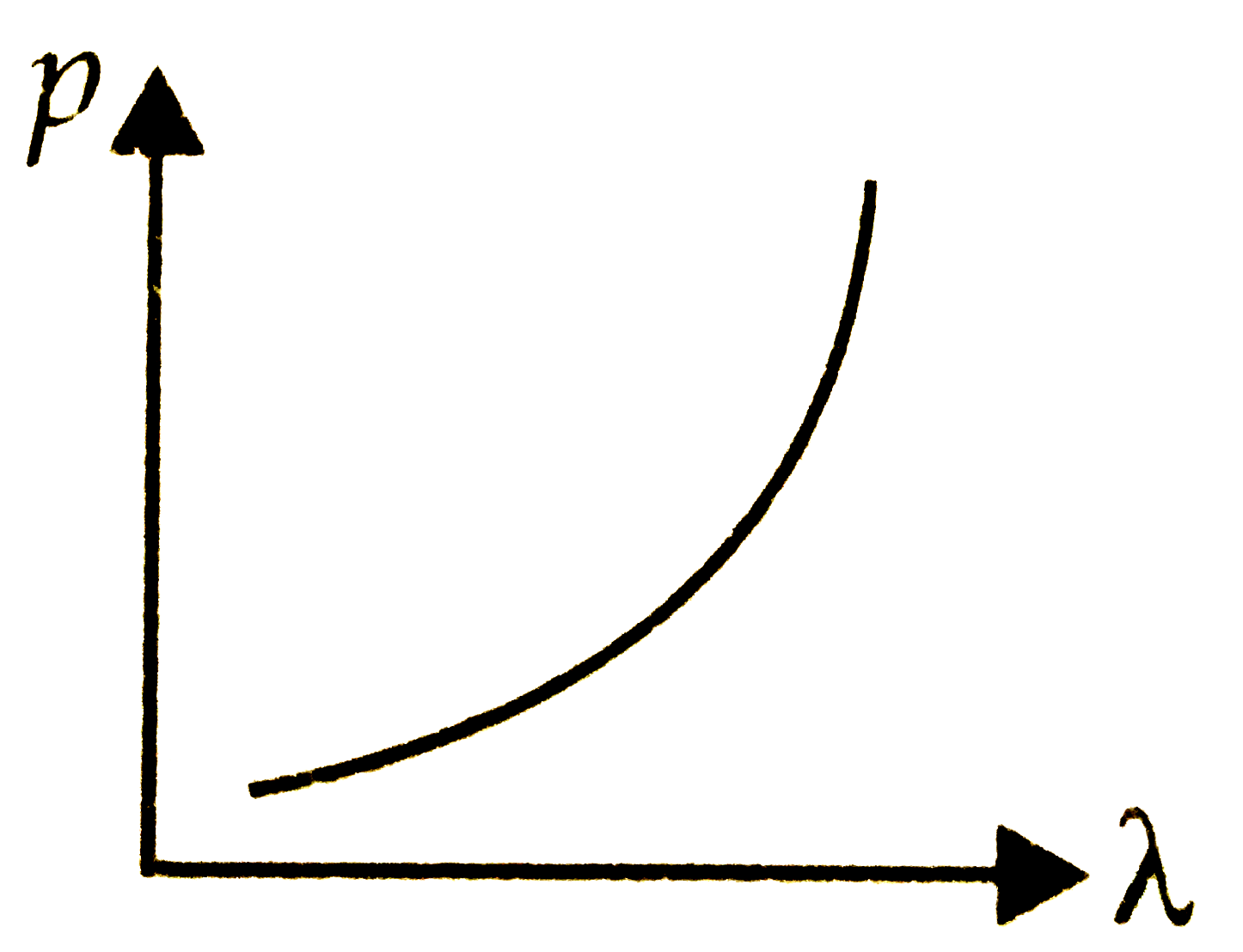 C
C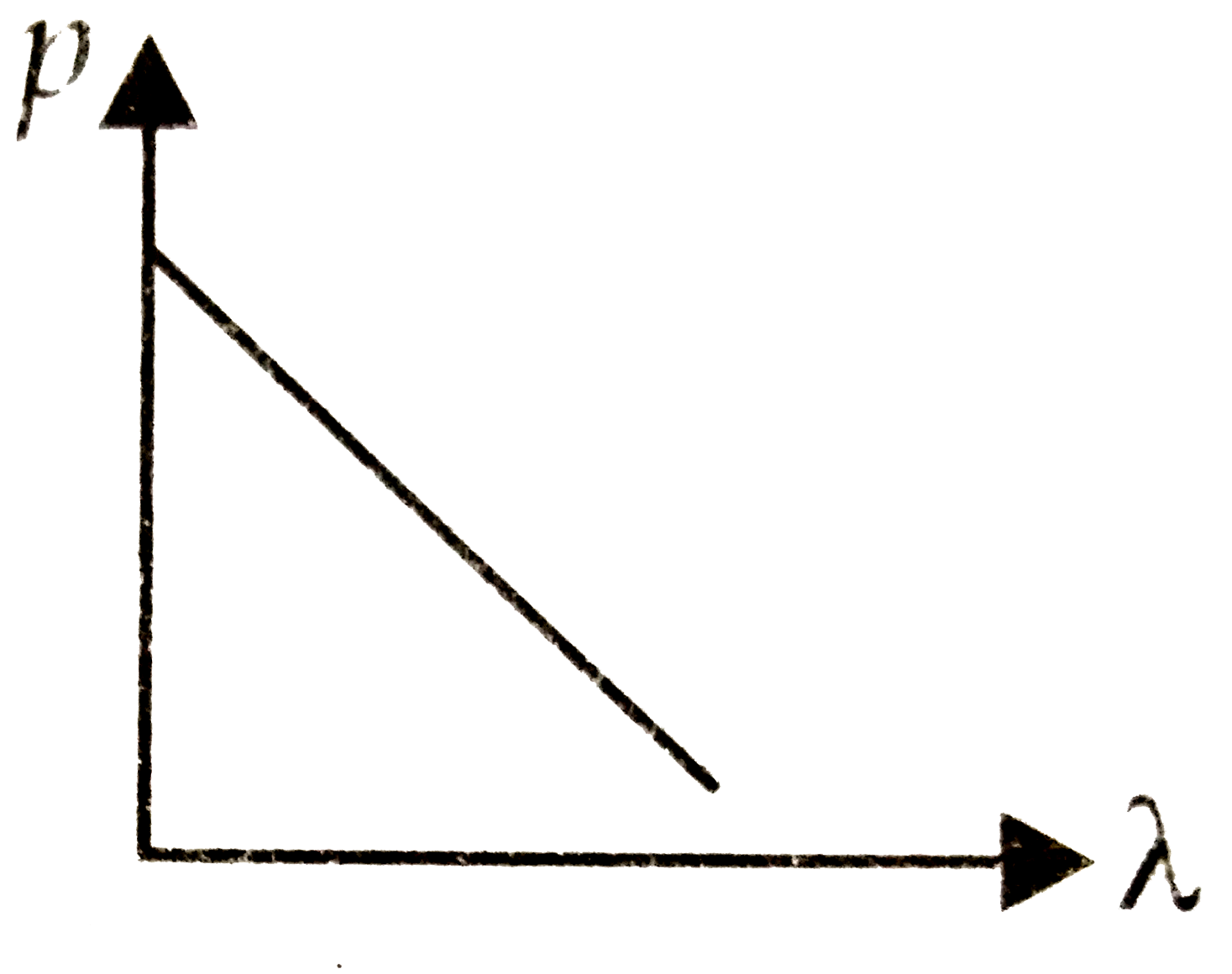 D
D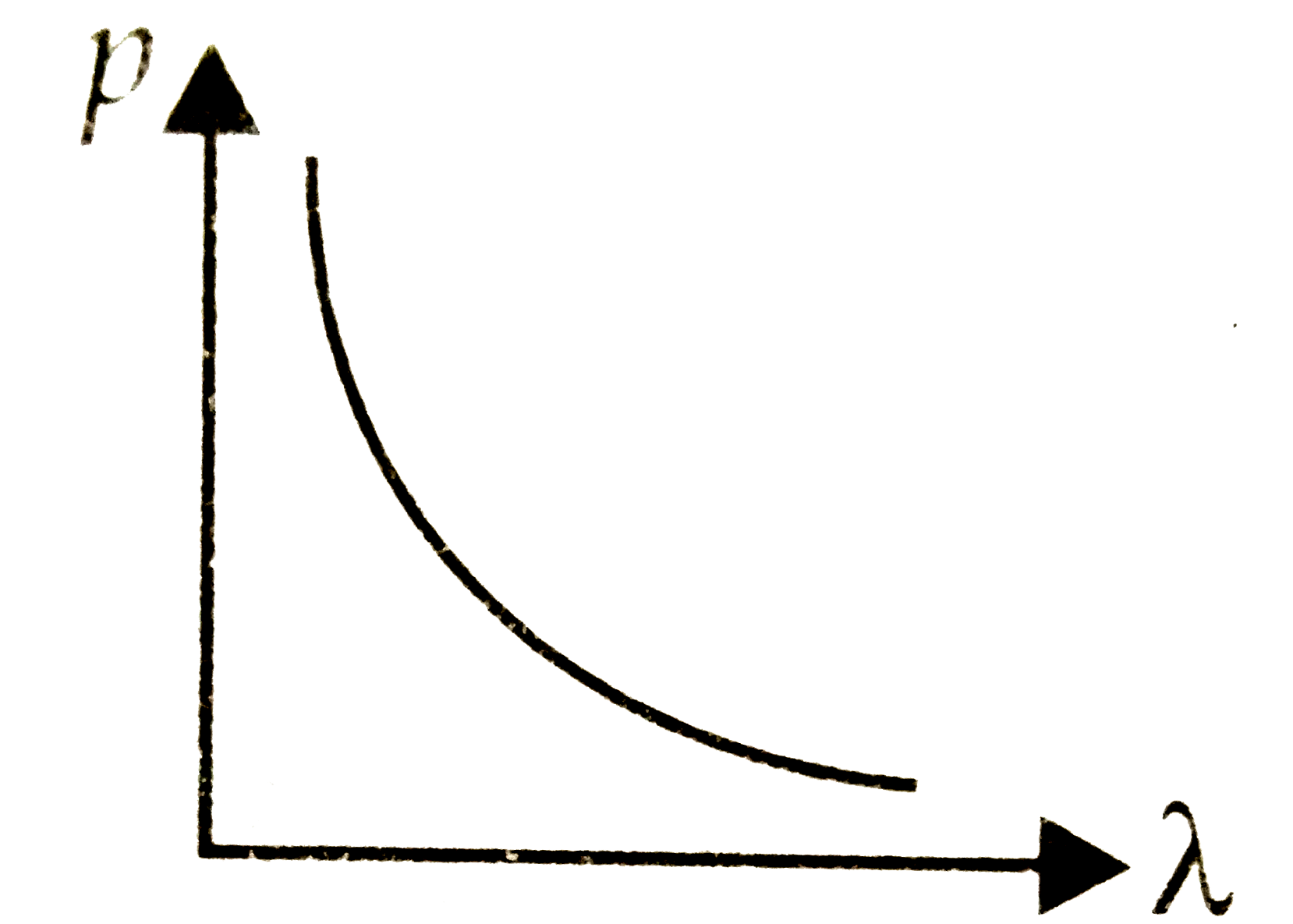
For particles having same K.E., the de-Broglie wavelength is
View SolutionCalculate the momentum of a particle which has de Broglie wavelength of 0.1 nm.
View SolutionThe momentum of a particle associated with de-Broglie's wavelength of 6Å is
View SolutionFor a given kinetic energy, which of the following has the smallest de Broglie wavelength : electron, proton and α−partic≤?
View SolutionIn which of the following conditions the de Broglie wavelength of particle A will be less than that of particle B(mA>mB)?
View SolutionIf the kinetic energy of a moving particle is E , then the de-Broglie wavelength is
View Solution
