In which of the following velocity (v) - time (1) graphs, the instantaneous acceleration decreases with time?
The correct Answer is:C
To determine in which of the given velocity-time graphs the instantaneous acceleration decreases with time, we need to analyze the slopes of the graphs. The slope of a velocity-time graph represents the acceleration. If the slope is decreasing, it indicates that the acceleration is also decreasing.
1. Understanding Instantaneous Acceleration:
- Instantaneous acceleration is defined as the rate of change of velocity with respect to time, mathematically expressed as a=dvdt.
- In a velocity-time graph, the slope of the graph at any point gives the instantaneous acceleration.
2. Analyzing Each Option:
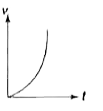
- Option 1: The graph shows a parabolic increase in velocity.
- As time increases, the slope of the graph (and thus the acceleration) is increasing. Therefore, the instantaneous acceleration is increasing, not decreasing.
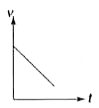
- Option 2: The graph shows a linear decrease in velocity.
- The slope is constant and negative, indicating constant negative acceleration. Since the acceleration is constant, it is neither increasing nor decreasing.
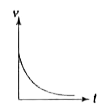
- Option 3: The graph shows a parabolic decrease in velocity.
- Here, as time increases, the slope of the graph decreases. This indicates that the instantaneous acceleration is decreasing as time progresses. This is a candidate for our answer.
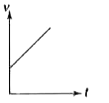
- Option 4: The graph shows a straight line increasing in velocity.
- The slope is constant and positive, indicating constant positive acceleration. Therefore, the instantaneous acceleration is constant and not decreasing.
3. Conclusion:
- Based on the analysis, the only graph where the instantaneous acceleration decreases with time is Option 3.
Final Answer:
The instantaneous acceleration decreases with time in Option 3.
- Instantaneous acceleration is defined as the rate of change of velocity with respect to time, mathematically expressed as a=dvdt.
- In a velocity-time graph, the slope of the graph at any point gives the instantaneous acceleration.
- Option 1: The graph shows a parabolic increase in velocity.
- As time increases, the slope of the graph (and thus the acceleration) is increasing. Therefore, the instantaneous acceleration is increasing, not decreasing.
- Option 2: The graph shows a linear decrease in velocity.
- The slope is constant and negative, indicating constant negative acceleration. Since the acceleration is constant, it is neither increasing nor decreasing.
- Option 3: The graph shows a parabolic decrease in velocity.
- Here, as time increases, the slope of the graph decreases. This indicates that the instantaneous acceleration is decreasing as time progresses. This is a candidate for our answer.
- Option 4: The graph shows a straight line increasing in velocity.
- The slope is constant and positive, indicating constant positive acceleration. Therefore, the instantaneous acceleration is constant and not decreasing.
- Based on the analysis, the only graph where the instantaneous acceleration decreases with time is Option 3.
The instantaneous acceleration decreases with time in Option 3.
Topper's Solved these Questions
- MISCELLANEOUS QUESTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - MISCELLANEOUS QUESTIONSEXERCISE - PART-B
99 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
- MOTIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - MOTIONEXERCISE - HIGHER ORDER THINKING QUESTIONS
48 Videos
Similar Questions
Graphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
For the given velocity-time graph the possibly correct acceleration-time relationship is

View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
The velocity-time graph for two objects P and Q are shown. The ratio of their respective acceleration is
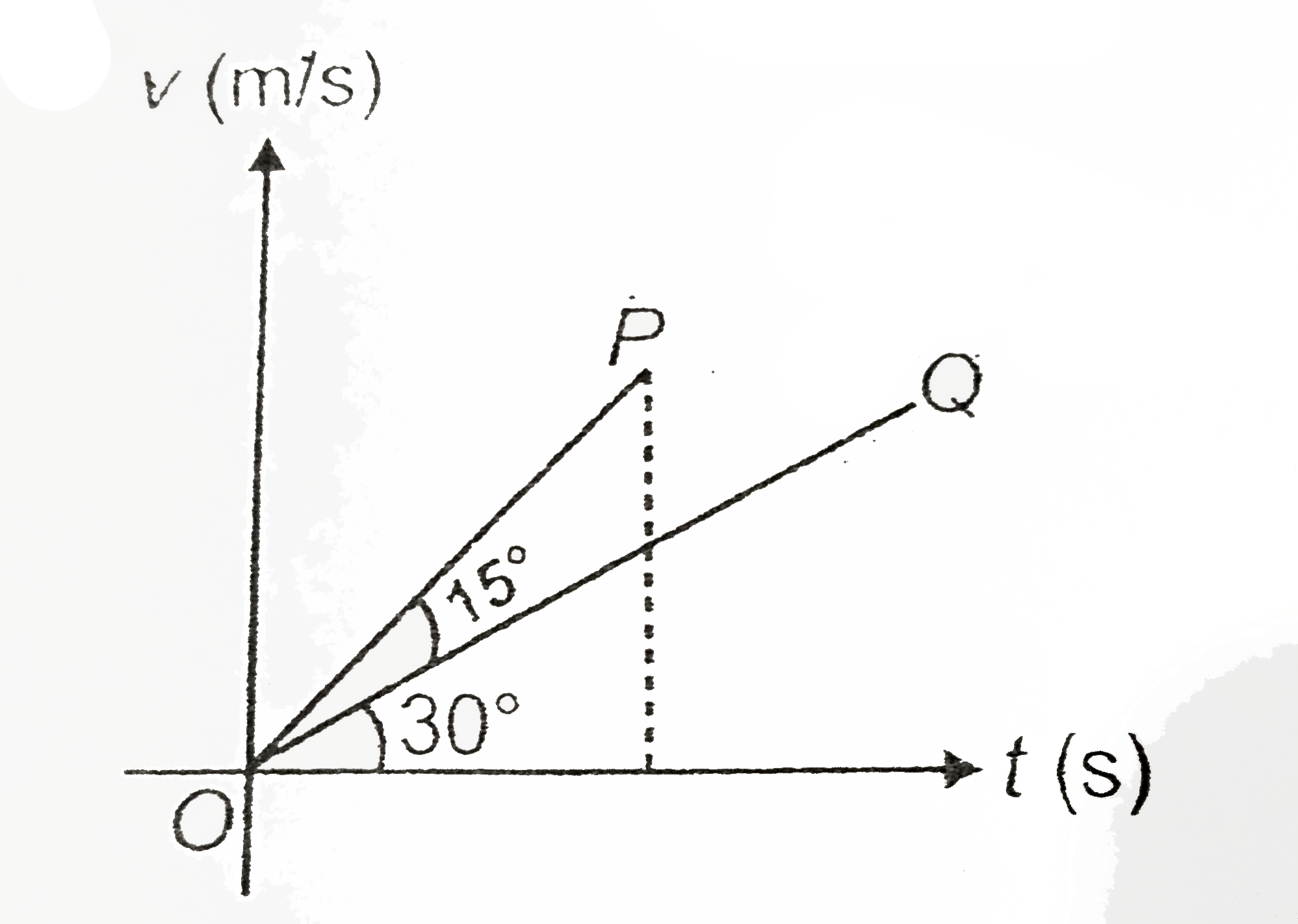
View Solution
Knowledge Check
In which of the following velocity (v) - time (t) graphs, the instantaneous acceleration decreases with time?
A B
B C
C D
D
Which of the following velocity-time graph is not possible?
A B
B C
C D
D
Which of the following shows velocity (v) - time (t) graph for falling apple?
A B
B C
C D
D
Which of the following shows the velocity (v) - time (t) graph for a falling apple?
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
For the above situation let t1 be the time of accelerated motion and t2 be the time or retarded motion, then the correct relation is
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
A car starts from rest with a constant acceleration a1 for some time and attains a velocity v0. Then it immediately retards at a constant rate a2 to rest. The total time to journey is t0 Identify the correct velocity-time graph
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
The correct relation between v0,a1,a2andt0 is
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
The average velocity of the car for the entire trip is
View Solution
