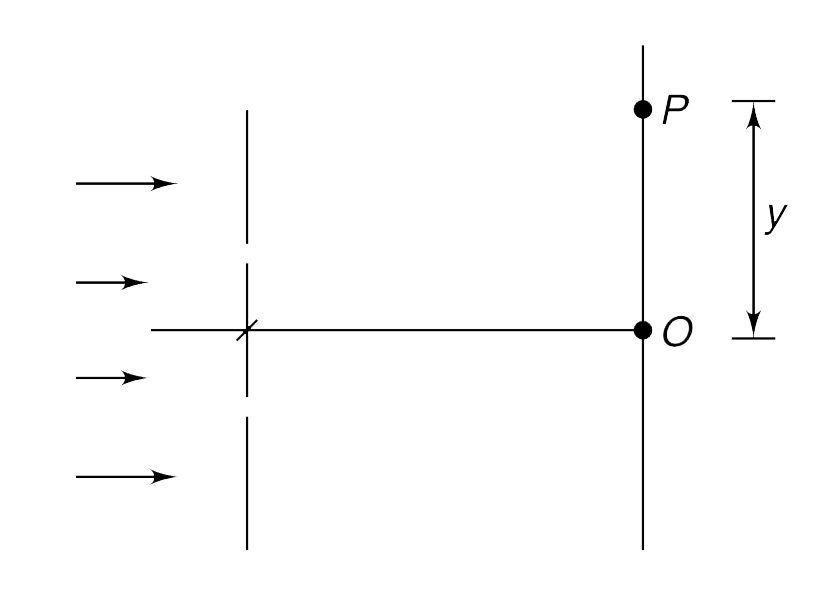
In young’s double slit experiment, when the slit plane is illuminated with light of wavelengthλ1, it was observed that point P is closest point from central maximum O, where intensity was 75% the intensity at O. When the light of wavelength λ2 is used, point P happens to be the nearest point from O where intensity is 50% of that at O. Find the ratioλ1λ2.
The correct Answer is:32
Step by step video, text & image solution for In young’s double slit experiment, when the slit plane is illuminated with light of wavelength lambda_(1), it was observed that point P is closest point from central maximum O, where intensity was 75% the intensity at O. When the light of wavelength lambda_(2) is used, point P happens to be the nearest point from O where intensity is 50% of that at O. Find the ratio(lambda_(1))/(lambda_(2)). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a Young's double slit experiment, using mono-chromatic light of wavelength λ, the intensity of light at a point on the screen where the path defference is λ is k units. Find the intensity at a point where the path difference is λ/3.
View SolutionIn a Young's double slit experiment, using mono-chromatic light of wavelength λ, the intensity of light at a point on the screen where the path defference is λ is k units. Find the intensity at a point where the path difference is λ/3.
View Solution
Knowledge Check
In Young’s double slit experiment, the 8 th maximum with wavelength λ1 is at a distance d1 from the central maximum and the 6 th maximum with a wavelength λ2 is at a distance d2. Then (d1/d2) is equal to
A43(λ2λ1)B43(λ1λ2)C34(λ2λ1)D34(λ1λ2)In young's double slit experiment using monochromatic light of wavelengths λ, the intensity of light at a point on the screen with path difference λ is M units. The intensity of light at a point where path difference is λ/3 is
AM2BM4CM8DM16In a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
A(a) Iocos(πx)βB(b) 4Iocos2(πx)βC(c) Iocos2(πx)βD(d) Io4cos2(πx)β
In Young's double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path diff. is λ is K units. Find the intensity of light at a point where path difference is λ/3.
View SolutionYoung's double slit experiment is conducted with light of wavelength λ.The intensity of the bright fringe is "1" .The intensity at a point where the path difference is3λ4 is given by
View SolutionIn Young's double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3 ?
View SolutionIn Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View Solution
