In Young's double-slit experiment, one of the slit is wider than other so that the amplitude of the light from one slit is double of that from other slit. If $I_{m}$ be the maximum intensity, the resultant intensity $I$ when they interfere at phase difference $ϕ$ is given by:

A

$\frac{I_{m}}{9} (1 + 8 \frac{{cos}^{2} (θ)}{2})$

B

$\frac{I_{m}}{9} (4 + 5 {cos}^{2} ϕ)$

C

$\frac{I_{m}}{3} (1 + 2 \frac{{cos}^{2} (ϕ)}{2})$

D

$\frac{I_{m}}{5} (1 + 3 \frac{{cos}^{2} (ϕ)}{2})$

Text Solution

Verified by Experts

The correct Answer is:A

Let $I_{1} and I_{2}$ be intensities which are coming from slits $S_{1} and S_{2}$
The resultant intensity
$∴ I = I_{1} + I_{2} + 2 \sqrt{I_{1} I_{2}} cos θ$
$I_{2} = K {(2 A)}^{2}$
$= 4 K A^{2}$
$∴ I_{2} = 4 I_{1}$

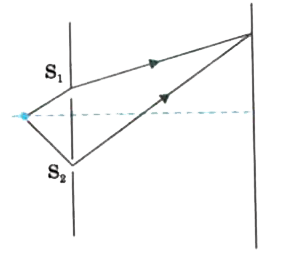
$I_{m} = I_{1} + I_{2} + 2 \sqrt{I_{1} I_{2}} {cos 0}^{\circ}$
$= I_{1} + 4 I_{1} + 2 \sqrt{4 I_{1}^{2}}$
$= I_{1} + 4 I_{1} + 2 \times 2 I_{1}$
$I_{m} = 9 I_{1} \Rightarrow I_{1} = \frac{I_{m}}{9} \Rightarrow I_{2} = \frac{4 I_{m}}{9}$
$I = \frac{I_{m}}{9} + \frac{4 I_{m}}{9} + 2 \sqrt{\frac{I_{m}}{9} \times \frac{4 I_{m}}{9}} cos θ$
$= \frac{I_{m}}{9} + \frac{4 I_{m}}{9} + 2 \sqrt{\frac{4 I_{m}^{2}}{81}} cos θ$
$= \frac{I_{m}}{9} (5 + 4 cos θ) = \frac{I_{m}}{9} (1 + 8 {cos}^{2} θ / 2)$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In Young's double slit experiment, one of the slit is wider than other, so that amplitude of the light from one slit is double of that from other slit. If $I_{m}$ be the maximum intensity, the resultant intensity I when they interfere at phase difference $ϕ$ is given by:
A $\frac{I_{m}}{9} (4 + 5 cos ϕ)$
B $\frac{I_{m}}{3} (1 + 2 {cos}^{2} (\frac{ϕ}{2})$
C $\frac{I_{m}}{5} (1 + 4 {cos}^{2} (\frac{ϕ}{2})$
D $\frac{I_{m}}{9} (1 + 8 {cos}^{2} (\frac{ϕ}{2})$
Question 2 - Select One
In Young's double slit experiment, one of the slit is wider than other, so that amplitude of the light from one slit is double of that from other slit. If $I_{m}$ be the maximum intensity, the resultant intensity I when they interfere at phase difference $ϕ$ is given by:
A $\frac{I_{m}}{3} (1 + 2 {cos}^{2} \frac{ϕ}{2})$
B $\frac{I_{m}}{5} (1 + 4 {cos}^{2} \frac{ϕ}{2})$
C $\frac{I_{m}}{9} (1 + 8 {cos}^{2} \frac{ϕ}{2})$
D $\frac{I_{m}}{9} (8 + {cos}^{2} \frac{ϕ}{2})$
Question 3 - Select One
In Young’s double slit experiment, one of the slits is so painted that intensity of light emitted from it is half of that of the light emitted from other slit. Then :
Afringe system will disappear
Bbright fringes will become brighter and dark fringes will be darker
Cboth bright and dark fringes will become darker
Ddark fringes will become less dark and bright fringes will become less bright

MODERN PUBLICATION-WAVE OPTICAL-OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)

Home
Ask Doubt
Profile