In young's double slit experiment the nth red bright band coincides with (n+1)th blue bright band. If the wavelength of red and blue lights are 7500A∘ and 5000A∘, the value of 'n' is
1
2
5
4
The correct Answer is:B
To solve the problem, we need to determine the value of 'n' in Young's double slit experiment where the nth red bright band coincides with the (n+1)th blue bright band. The wavelengths of the red and blue lights are given as 7500 Å and 5000 Å respectively.
1. Understanding the Problem:
We have two different wavelengths of light: red (λ_red = 7500 Å) and blue (λ_blue = 5000 Å). The nth red bright band coincides with the (n+1)th blue bright band.
2. Fringe Width Formula:
In Young's double slit experiment, the position of bright fringes is given by the formula:
yn=nλDd
where yn is the position of the nth bright fringe, λ is the wavelength of light, D is the distance from the slits to the screen, and d is the distance between the slits.
3. Setting Up the Equation:
For red light, the position of the nth bright band is:
yredn=nλredDd=n7500Dd
For blue light, the position of the (n+1)th bright band is:
ybluen+1=(n+1)λblueDd=(n+1)5000Dd
4. Equating the Positions:
Since the nth red band coincides with the (n+1)th blue band, we can set the two equations equal to each other:
n7500Dd=(n+1)5000Dd
5. Cancelling Common Terms:
The terms D and d can be cancelled from both sides:
n⋅7500=(n+1)⋅5000
6. Expanding the Equation:
Expanding the right-hand side gives:
7500n=5000n+5000
7. Rearranging the Equation:
Rearranging the equation to isolate n:
7500n−5000n=5000
2500n=5000
8. Solving for n:
Dividing both sides by 2500:
n=50002500=2
Final Answer:
The value of n is 2.
We have two different wavelengths of light: red (λ_red = 7500 Å) and blue (λ_blue = 5000 Å). The nth red bright band coincides with the (n+1)th blue bright band.
In Young's double slit experiment, the position of bright fringes is given by the formula:
yn=nλDd
where yn is the position of the nth bright fringe, λ is the wavelength of light, D is the distance from the slits to the screen, and d is the distance between the slits.
For red light, the position of the nth bright band is:
yredn=nλredDd=n7500Dd
For blue light, the position of the (n+1)th bright band is:
ybluen+1=(n+1)λblueDd=(n+1)5000Dd
Since the nth red band coincides with the (n+1)th blue band, we can set the two equations equal to each other:
n7500Dd=(n+1)5000Dd
The terms D and d can be cancelled from both sides:
n⋅7500=(n+1)⋅5000
Expanding the right-hand side gives:
7500n=5000n+5000
Rearranging the equation to isolate n:
7500n−5000n=5000
2500n=5000
Dividing both sides by 2500:
n=50002500=2
The value of n is 2.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) (straight objective Type Questions)31videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions4videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)97videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
In an interference pattern the (n+4)th blue bright fringe and nth red bright fringe are formed at the same spot. If red and blue light have the wavelength of 7800Å and 5200Å then value of n should be-
View SolutionIn Young.s double slit experiment, what is the path difference between the two light waves forming 5th bright band (fringe) on the screen ?
View Solution
Knowledge Check
- Question 1 - Select One
In a Young's double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case
Athere shall be alternate interference patterns of red and blueBthere shall be an interference pattern for red distinct from that for blueCthere shall be no interference fringesDthere shall be an interference pattern for red mixing with one for blue.
In Young's double slit experiment, the wavelength of red light is 7800Å. The value of n for which nth bright band due to red light coincides with (n+1)th bright band due to blue light(λ=5200Angstrom), is
View SolutionIn Young.s double slit experiment sodium light is replaced by blue lamp, then the fringe width
View SolutionIn a Young's double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the 11th bright fringe on the other side, as measured from Q. If the wavelength of the light used is 600nm. Then S1B will be equal to
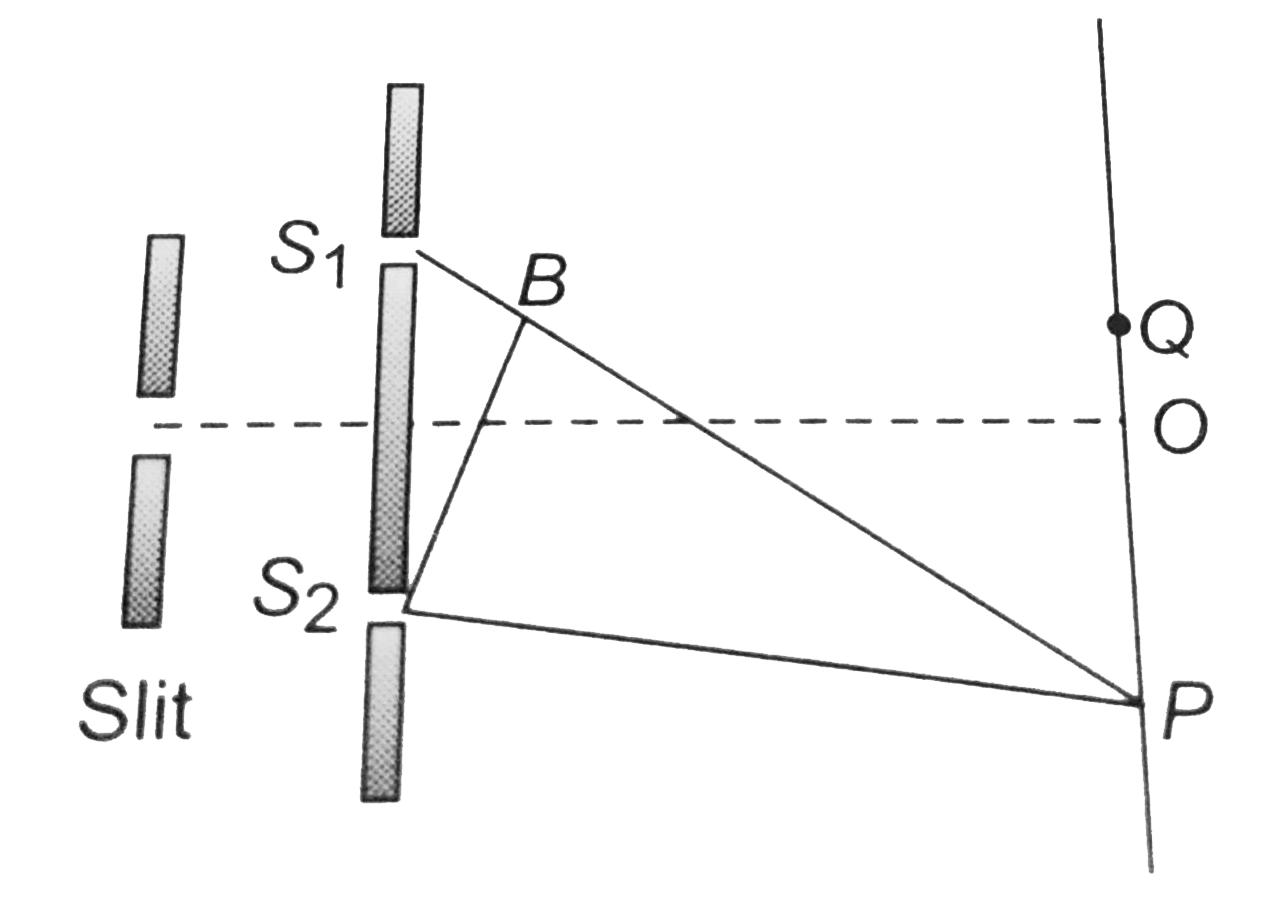 View Solution
View SolutionIn Young's double - slit experiment intensity at a point is (1/4)th of the maximum intensity. The possible angular position of this point is
View SolutionIn Young's double-slit experiment, the ratio of intensities of a bright band and a dark band is 16:1. The ratio of amplitudes of interfering waves will be
View SolutionA : In Young.s double slit expriment the band width for red colour is more
R : Wavelength of red is small among the colours of white light.View Solution
