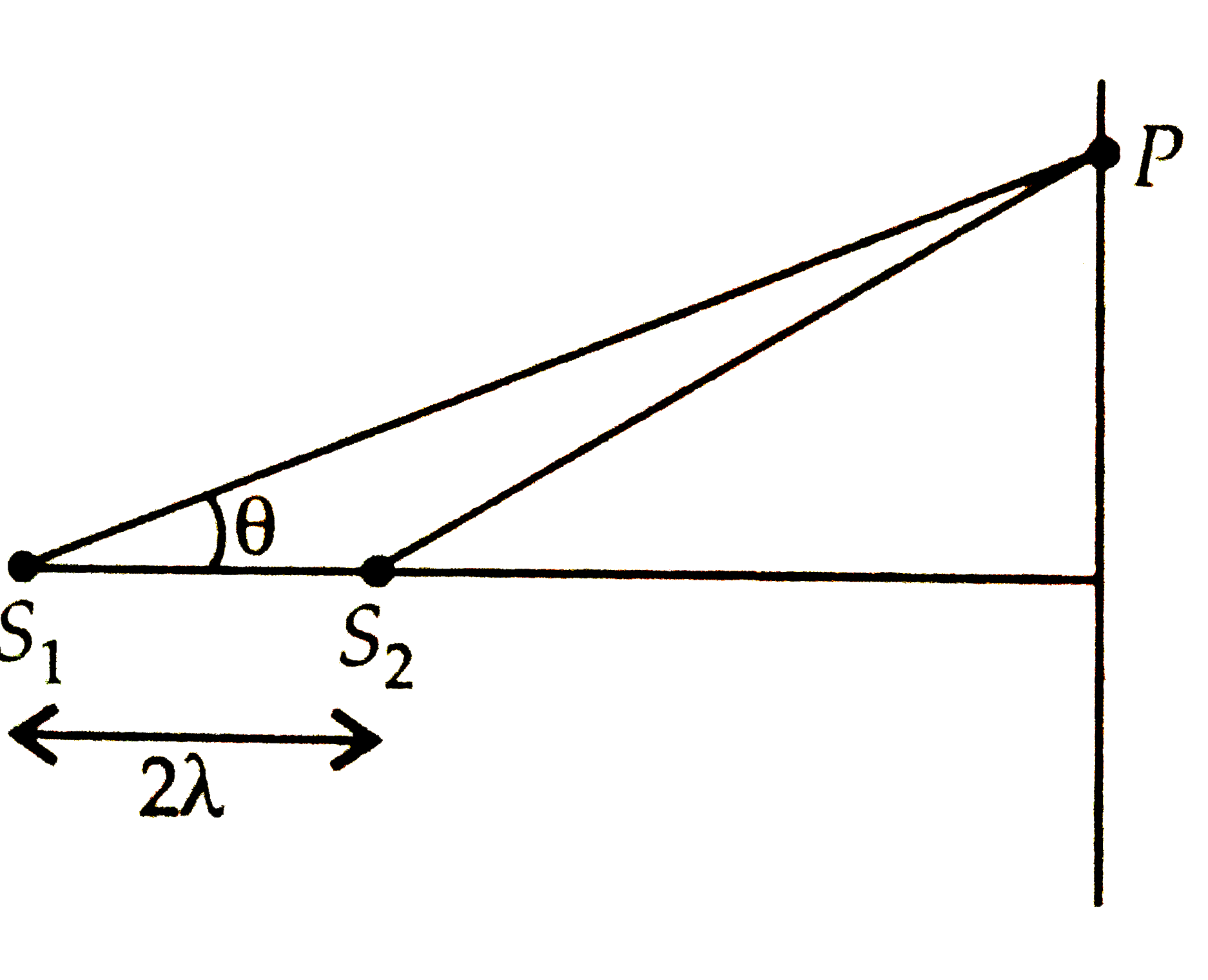
In Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is $\frac{3}{4} I_{0}$ ,where $I_{0}$ is the maximum intensity.
Then the value of $θ$ is,
(Given the distance between the two slits $S_{1}$ and $S_{2}$ is $2 λ$ )

A

${cos}^{- 1} (\frac{1}{12})$

B

${sin}^{- 1} (\frac{1}{12})$

C

${tan}^{- 1} (\frac{1}{12})$

D

${sin}^{- 1} (\frac{3}{5})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Here $\frac{I}{I_{0}} = \frac{3}{4}$ (given)
$\Rightarrow {cos}^{2} (\frac{ϕ}{2}) = \frac{3}{4} (∵ I = I_{0} {cos}^{2} (\frac{ϕ}{2}))$
$or cos \frac{ϕ}{2} = \frac{\sqrt{3}}{2} or ϕ = 60^{\circ} = \frac{π}{3}$
Phase difference $ϕ = \frac{2 π}{λ} \times$ path difference
From the figure, pathe difference is
d $cos θ = 2 λ cos θ (∵ d = 2 λ)$
$∴ \frac{π}{3} = \frac{2 π}{λ} 2 λ cos θ$
$∴ cos θ = \frac{1}{12}$
$∴ θ = {cos}^{- 1} (\frac{1}{12})$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a Young's double slit experiment the amplitudes of the two waves incident on the two slits are $A$ and $2 A$ . If $I_{0}$ is the maximum intensity, then the intensity at a spot on the screen where the phase difference between the two interfering waves is $ϕ$ .
A $I_{0} {cos}^{2} (ϕ / 2)$
B $\frac{I_{0}}{3} {sin}^{2} (ϕ / 2)$
C $(\frac{I_{0}}{9} (5 + 4 cos (ϕ))$
D $\frac{I_{0}}{9} (5 + 8 cos (ϕ))$
Question 2 - Select One
In Young's double slit experiment intensity at a point is $(\frac{1}{4})$ of the maximum intersity. Angular position of this point is
A ${sin}^{- 1} (\frac{λ}{d})$
B ${sin}^{- 1} (\frac{λ}{2 d})$
C ${sin}^{- 1} (\frac{λ}{3 d})$
D ${sin}^{- 1} (\frac{λ}{4 d})$
Question 3 - Select One
In Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is $λ$ and d is the distance between the slits, the angular separation between point P and the center of the screen is
A ${sin}^{- 1} (\frac{λ}{d})$
B ${sin}^{- 1} (\frac{λ}{2 d})$
C ${sin}^{- 1} (\frac{λ}{3 d})$
D ${sin}^{- 1} (\frac{λ}{4 d})$

NCERT FINGERTIPS-WAVE OPTICS-Interference Of Light Waves And Young'S Experiment

Home
Ask Doubt
Profile