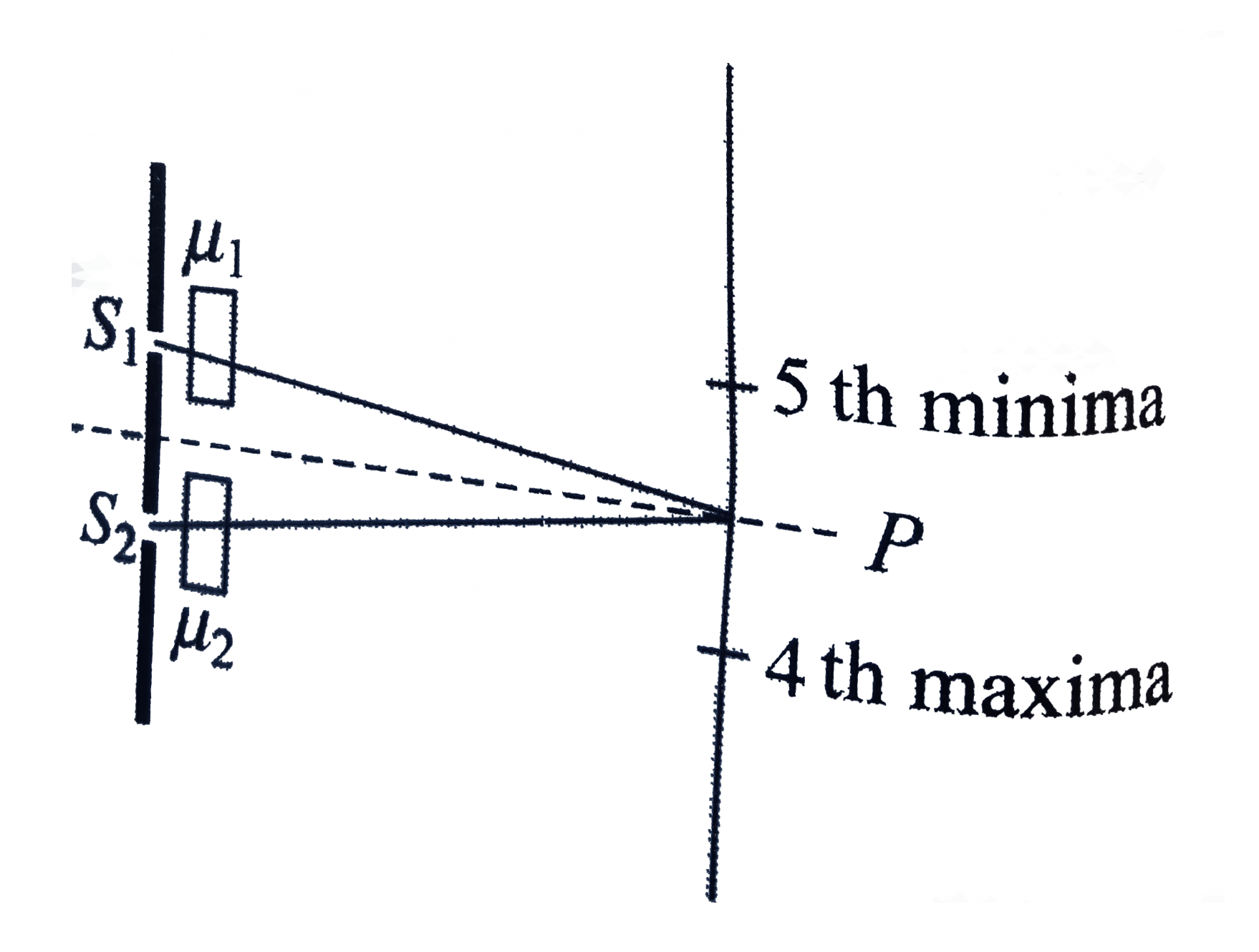
In Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
Path difference between two waves starting from S1 and S2 and reaching at P,
Δ=(μ2−μ1)t In the absence of plate, phase difference between two waves reaching at P equals zero. When the plates are introduced, let the phase difference between waves at P be δ.
As the waves are of point of equal amplitude (or intensity), so initial intensity at P,
I0=(a1+a2)2=4a2
New intensity at P is
I0=(a1+a2)2=(2a)2=4a2
New Intensity at P is
I=34I0=34×4a2=3a2
We have,
I=a21+a22+2a1a2cosδ
⇒3a2=a2+a2+2a2cosδ
This gives
δ=π3,5π3,7π3,...=(2mπ±π3),m=1,2,3,...
shift of interference pattern upward due to glass plate,
1=Dd(μ1−1)t=Dd(1.7−1)t
Net shift downward is
Dd(μ2−μ1t)=Dd(1.7−1.4)t=Dd(0.3t)
From given conditions,
Dd(0.3t)>5λDd and Dd(0.3t)<(6−12)λd
⇒5λ0.3<t<11λ2×0.3
λ5400Å=5.4×10−7m
Path difference created at P due to both the plates is (μ2−(μ1)t.
Also, path difference,
Δ=λ2π× phase difference
⇒(μ2−μ1)t=λ2πδ
or 0.3t=λ2π×(2mπ±π3)
=(m±16)λ
=(m±16)×5.4×10−7m
From Eqs. (ii) and (iii), we have (putting m = 5),
t=(5+16)×5.4×10−70.3
=93×10−7 m taking (+) sign
=87×10−7 m taking (−) sign
In view of Eq. (ii),
t=93×10−7m=9.3×10−6m=9.3μm
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - QUESTION BANK
37 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
In Young’s experiment, the upper slit is covered by a thin glass plate of refractive index 1.4, while the lower slit is covered by another glass plate having the same thickness as the first one but having the refractive index 1.7. Interference pattern is observed using light of
wavelength 5400 Å . It is found that the point P on the screen where central maximum (n = 0) fall before the glass plate were inserted, now has % the original intensity. It is further observed that what used to be the fifth maximum earlier lies below the point P while the sixth minima lies above P. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected).
View SolutionIn Young’s double slit experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having same thickness as the first one but having refractive index 1.7.
Interference pattern is observed using light of wavelength5400∘A. It is found that the point P on the screen where the central maximum fell before the glass plates were inserted, now has 34 the original intensity. It is also observed that what used to be 5th maximum earlier, lies below the point P while the6th minimum lies above P. Calculate the thick- ness of glass plates. Absorption of light by glass plate may be neglected.
View Solution
Knowledge Check
In young's experiment, the upper slit is covered by a thin glass plate of refractive index 43 and of thickness 9λ, where λ is the wavelength of light used in the experiment. The lower slit is also covered by another glass plate of thickness 2D & refractive index 32, as shown in figure. If I0 is the intensity at point P due to slits S1 & S2 each, then:
 AIntensity at point P is 4I0BTwo fringes have been shifted in upward direction after inserted of both the glass plates together.COptical path difference between te waves from S1 & S2 at point P is 2λDIf the source S is shifted upwards by a small distance d2 then the fringe originally at P after inserting the plates, shifts downwards by D(d2d1)
AIntensity at point P is 4I0BTwo fringes have been shifted in upward direction after inserted of both the glass plates together.COptical path difference between te waves from S1 & S2 at point P is 2λDIf the source S is shifted upwards by a small distance d2 then the fringe originally at P after inserting the plates, shifts downwards by D(d2d1)In Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
A(a) 1.75B(b) 1.50C(c) 1.25D(d) 1.00In Young's double slit experiment, the fringes are displaced by a distance x when a glass plate of one refractive index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
A1.75B1.5C1.25D1
In a Young's experimenttje upper slit is covered by a thin glass plate of refractive index. 1.4 while the lower slit is covered with another glass plate, having the same thickness as the first one but having refravtive index 1.7. Interference pattern is observed using light of wavelength 5400Å. It is found that the point P on the sreen where the central where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fifth maximum earlie, lies shown the point P while the sixth minimum lies above P. Calculate the thickness of glass plate. (Absorption of light by a glass may be neglected).
View SolutionIn a Young's experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having the same thickness as the first ont but having refractive index 1.7. Interference pattern is observed using light of wavelength 5400A. It is found that the point P on the screen where the central maximum fell berore the glass were inserted now has (3/4)th the original intensity. It is further observed that what used to be the 5th maximum earlier, Iies below the point O while the 6th minimum lies above O. The thickness of the glass plate in n×10−7m. Find the value of n
(Absorption of light by glass plate may by neglected)
View SolutionIn Young's double-slit experiment, if both the slits are covered by a thin transparent sheet of thickness t and refractive index n, the optical path difference between the two interfering waves
View SolutionIn double slit experiment fringes are obtained using light of wavelength 4800Å One slit is covered with a thin glass film of refractive index. 1.4 and another slit is covered by a film of same thickness but refractive index 1.7. By doing so, the central fringe is shifted to fifth bright fringe in the original pattern. The thickness of glass film is
View SolutionIn Young's double slit experiment, one slit is covered with red filter and another slit is covered by green filter, then interference pattern will be
View Solution
