Is it necssary to express all angles in radianwhile using the equation ω=ω0+αt?
To determine whether it is necessary to express all angles in radians while using the equation ω=ω0+αt, we can analyze the units involved in the equation.
1. Understanding the Equation:
The equation ω=ω0+αt relates the final angular velocity (ω), initial angular velocity (ω0), angular acceleration (α), and time (t).
2. Identifying Units:
- The unit of angular velocity (ω) and (ω0) is radians per second (rad/s).
- The unit of angular acceleration (α) is radians per second squared (rad/s²).
- The unit of time (t) is seconds (s).
3. Dimensional Consistency:
For the equation to be dimensionally consistent, all terms must have the same units.
- The term αt must have the same unit as ω and ω0.
- Since α is in rad/s² and t is in seconds, the product αt results in:
(rad/s²)×(s)=(rad/s)
This shows that αt will yield a unit of radians per second, which is consistent with the units of ω and ω0.
4. Conclusion:
Since the units of angular velocity are defined in terms of radians, it is necessary to express all angles in radians when using the equation ω=ω0+αt to ensure dimensional consistency.
5. Conversion from Degrees to Radians:
If you have angles in degrees and need to convert them to radians, you can use the conversion factor:
Radians=Degrees×π180
This conversion is essential when you are working with angular quantities in this equation.
The equation ω=ω0+αt relates the final angular velocity (ω), initial angular velocity (ω0), angular acceleration (α), and time (t).
- The unit of angular velocity (ω) and (ω0) is radians per second (rad/s).
- The unit of angular acceleration (α) is radians per second squared (rad/s²).
- The unit of time (t) is seconds (s).
For the equation to be dimensionally consistent, all terms must have the same units.
- The term αt must have the same unit as ω and ω0.
- Since α is in rad/s² and t is in seconds, the product αt results in:
(rad/s²)×(s)=(rad/s)
This shows that αt will yield a unit of radians per second, which is consistent with the units of ω and ω0.
Since the units of angular velocity are defined in terms of radians, it is necessary to express all angles in radians when using the equation ω=ω0+αt to ensure dimensional consistency.
If you have angles in degrees and need to convert them to radians, you can use the conversion factor:
Radians=Degrees×π180
This conversion is essential when you are working with angular quantities in this equation.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A solid body rotates about a stationary axis, so that its angular velocity depends on the rotational angle ϕ as ω=ω0−kϕ where ω0 and K are positive constants. At the moment t=0,ϕ=0 Find the dependence of rotation angle.
View SolutionEquation of a standing wave is generally expressed as y=2Asinωtcoskx. In the equation quantity ωk represents
View Solution
Knowledge Check
18−3ww+6=w2w+6
Which of the following represents the sum of all possible solutions to the equation above?A−9B−3C3D9
A liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
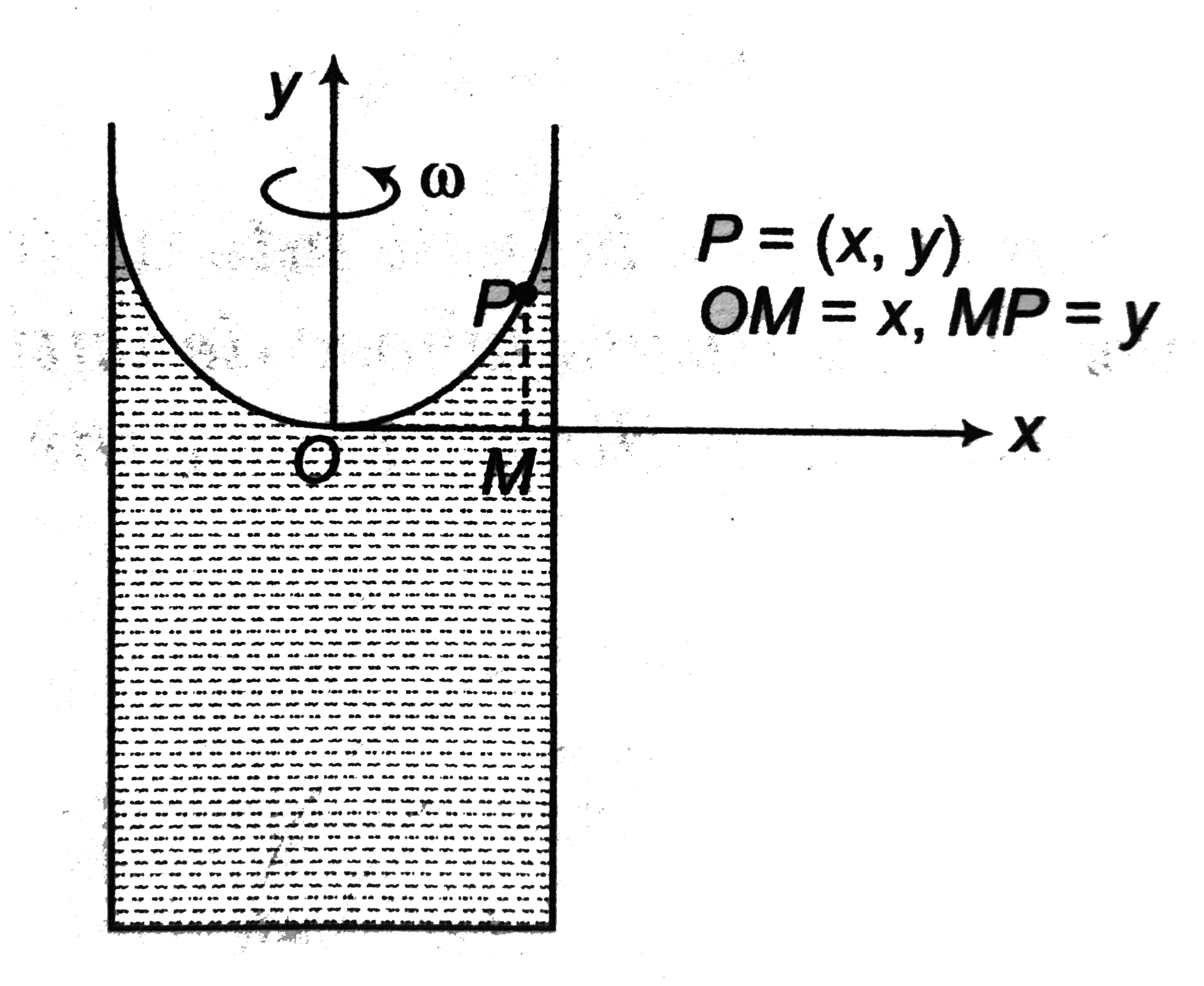 .
.
View SolutionIf ω is a complex cube root of unity, then the equation |z−ω|2+∣∣z−ω2∣∣2=λ will represent a circle, if
View SolutionIf ω is an imaginary cube root of unity then the equation whose roots are 2ω+3ω2 and 2ω2+3ω is
View SolutionIf ω is a complex cube root of unity, then the equationi |z−ω|2+∣∣z−ω2∣∣2=γ represent a circle, if
View SolutionFind number of values of complex numbers ω satisfying the system of equation z3=−(¯¯ω)7 and z5.ω11=1
View SolutionThe SHM of a particle is given by the equation x=2sinωt+4cosωt. Its amplitude of oscillation is
View SolutionIf ω is a complex cube root of unity, then a root of the equation
∣∣ ∣ ∣∣x+1ωω2ωx+ω21ω21x+ω∣∣ ∣ ∣∣=0, is
View Solution