It is known from Curie's law that magnetic moment (m) of a paramagnetic sample is directly proporational to the ratio of the external magnetic field (B) to the absolute temperature (T). A sample of paramagnetic salt contains atomic dipoles each of dipole moment .
Sample is placed under a homogeneous magnetic field of and cooled to a temperature of 4.2. The drgree of magnetic saturation achevied is equal to . You may assume that dipoles are randomly oriented and do not contributes to the magnetisation . The total diploe moment of the sample , for a magnetic field of and a temperature of , is
The correct Answer is:C
To solve the problem step by step, we will follow the instructions given in the video transcript while ensuring clarity and understanding.
1. Calculate the Total Dipole Moment (m1) at the Initial Conditions:
- Given:
- Number of atomic dipoles, N=2.0×1024
- Dipole moment of each dipole, p=1.5×10−23J/T
- Degree of magnetic saturation, S=15%=0.15
- The total dipole moment m1 can be calculated as:
m1=N⋅p⋅S
m1=(2.0×1024)⋅(1.5×10−23)⋅0.15
m1=2.0×1.5×0.15×1024−23=0.45×101=4.5J/T
2. Use Curie’s Law to Relate the Magnetic Moments:
- According to Curie's law, the ratio of the magnetic moments at two different conditions can be expressed as:
m1m2=B1B2⋅T2T1
- Where:
- B1=0.84T (initial magnetic field)
- B2=0.98T (final magnetic field)
- T1=4.2K (initial temperature)
- T2=2.8K (final temperature)
3. Rearranging to Find m2:
- Rearranging the equation gives:
m2=m1⋅B2B1⋅T1T2
- Substituting the known values:
m2=4.5⋅0.980.84⋅4.22.8
4. Calculating m2:
- First, calculate the ratios:
0.980.84≈1.1667
4.22.8=1.5
- Now substitute these ratios back into the equation:
m2=4.5⋅1.1667⋅1.5
m2≈4.5⋅1.75≈7.875J/T
5. Final Result:
- The total dipole moment of the sample at the new conditions is approximately:
m2≈7.9J/T
- Given:
- Number of atomic dipoles, N=2.0×1024
- Dipole moment of each dipole, p=1.5×10−23J/T
- Degree of magnetic saturation, S=15%=0.15
m1=N⋅p⋅S
m1=(2.0×1024)⋅(1.5×10−23)⋅0.15
m1=2.0×1.5×0.15×1024−23=0.45×101=4.5J/T
- According to Curie's law, the ratio of the magnetic moments at two different conditions can be expressed as:
m1m2=B1B2⋅T2T1
- Where:
- B1=0.84T (initial magnetic field)
- B2=0.98T (final magnetic field)
- T1=4.2K (initial temperature)
- T2=2.8K (final temperature)
- Rearranging the equation gives:
m2=m1⋅B2B1⋅T1T2
- Substituting the known values:
m2=4.5⋅0.980.84⋅4.22.8
- First, calculate the ratios:
0.980.84≈1.1667
4.22.8=1.5
- Now substitute these ratios back into the equation:
m2=4.5⋅1.1667⋅1.5
m2≈4.5⋅1.75≈7.875J/T
- The total dipole moment of the sample at the new conditions is approximately:
m2≈7.9J/T
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A sample of paramagnetic salt contains 2×1024 atomic dipoles, each of moment 1.5×10−23JT−1. The sample is placed under a homogeneous magnetic field of 0.64T and cooled to a temperature of 4.2K. The degree of magnetic saturation archieved is equal to 15%. What is the total dipole moment of the sample for a mangetic field of 0.98T and a temperature of 2.8K. (Assume Curie's law).
View SolutionA sample of paramagnetic salt contains 2×1024 atomic dipoles, each of moment 1.5×10−23JT−1. The sample is placed under a homogeneous magnetic field of 0.64T and cooled to a temperature of 4.2K. The degree of magnetic saturation archieved is equal to 15%. What is the total dipole moment of the sample for a mangetic field of 0.98T and a temperature of 2.8K. (Assume Curie's law).
View SolutionWith reference to magnetic dipole, match the tems of Column I with the tems of Column Ii and Choose the correct option from the codes given below.

View SolutionThe dipole moment of
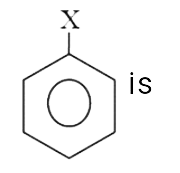 is 1.5 D.
is 1.5 D.
The dipole moment of is
is
View SolutionAccording to Curie's law, the magnetic susceptibilty of a paramagnetic substance at an absolute temperature T is proportional to
View SolutionAccording to Curie's law, the magnetic susceptibilty of a paramagnetic substance at an absolute temperature T is proportional to
View SolutionDipole moment of
 is 1.5D. The dipole moment of
is 1.5D. The dipole moment of
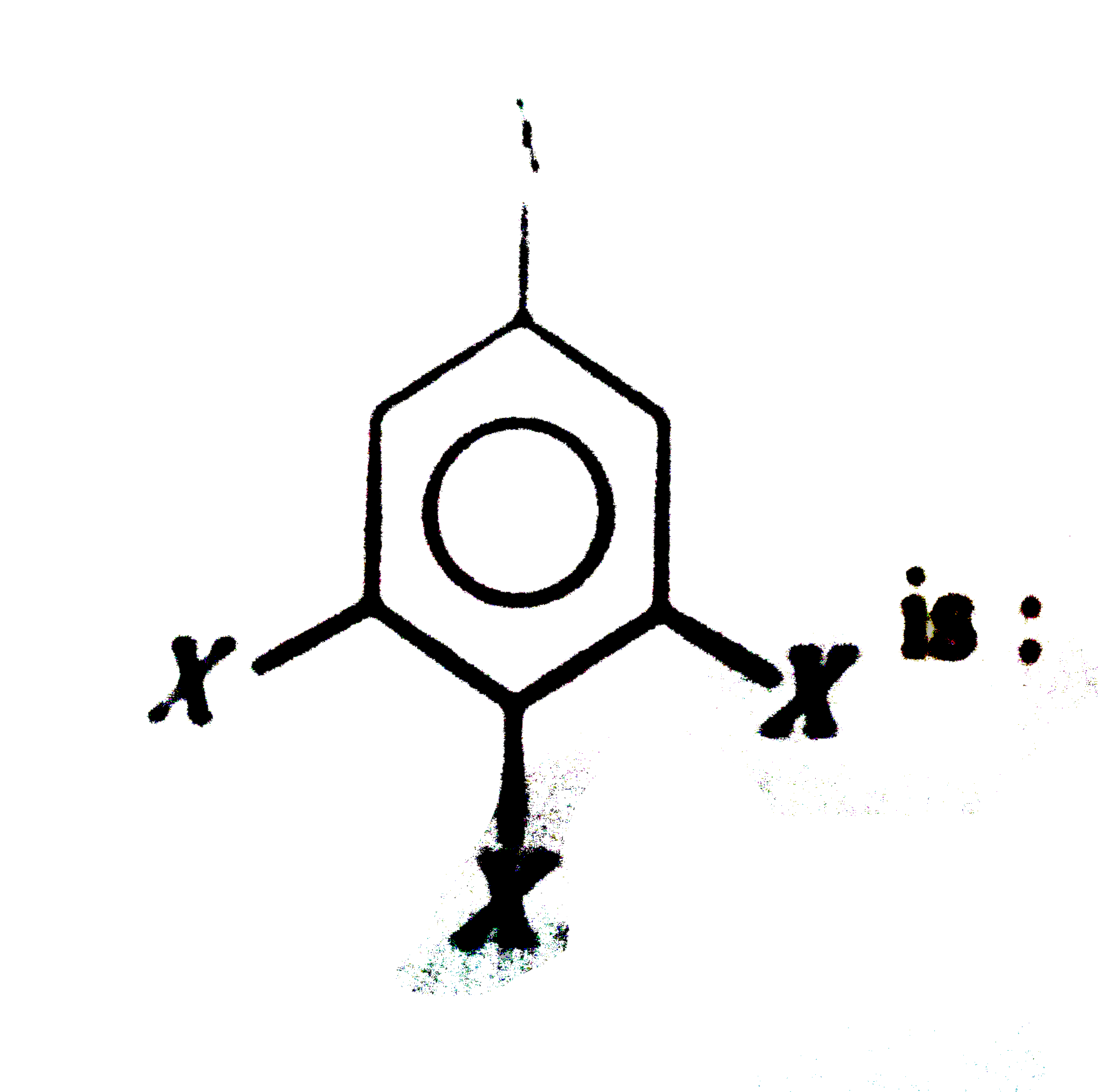
View SolutionA paramagnetic sample shows a net magnetisationo f 6 A/m when it is placed in an external magnetic field of 0.4 T at a temperature of 4 K. When the sample is placed in an external magnetic field of 0.3 T at a temperature of 24 K, then the magnetisation will be :
View SolutionA sample of vitamin C is known to contain 2.58×1024 oxygen atoms. How many molesof oxygen atoms are present in the sample?
View SolutionA sample of sucrose is found to contain 72.28×1021 atoms of carbon. Find the mass of the sample in grams.
View Solution
