Length of wire at room temperature is 4.55 m , when the temperature increases up to 100∘C then its length becomes 4.57 m . The coefficient of linear expansion (α) of the given wire is
5.021×10−5K−1
6.021×10−5K−1
7.021×10−5K−1
8.021×10−5K−1
The correct Answer is:D
To find the coefficient of linear expansion (α) of the wire, we can use the formula:
ΔL=L0⋅α⋅ΔT
Where:
- ΔL is the change in length of the wire,
- L0 is the original length of the wire,
- α is the coefficient of linear expansion,
- ΔT is the change in temperature.
Step 1: Identify the given values
- Original length of the wire, L0=4.55m
- New length of the wire, L=4.57m
- Change in length, ΔL=L−L0=4.57m−4.55m=0.02m
- Initial temperature, T1=27∘C (room temperature)
- Final temperature, T2=100∘C
- Change in temperature, ΔT=T2−T1=100∘C−27∘C=73∘C
Step 2: Convert temperature change to Kelvin
Since the change in temperature in Celsius is the same as in Kelvin, we can directly use:
ΔT=73K
Step 3: Substitute the values into the formula
Now, substituting the values into the formula for ΔL:
0.02=4.55⋅α⋅73
Step 4: Solve for α
Rearranging the equation to solve for α:
α=0.024.55⋅73
Calculating the denominator:
4.55⋅73=332.15
Now substituting this back into the equation for α:
α=0.02332.15≈6.021×10−5K−1
Final Answer
The coefficient of linear expansion α of the given wire is approximately:
α≈6.021×10−5K−1
---
- ΔL is the change in length of the wire,
- L0 is the original length of the wire,
- α is the coefficient of linear expansion,
- ΔT is the change in temperature.
- Original length of the wire, L0=4.55m
- New length of the wire, L=4.57m
- Change in length, ΔL=L−L0=4.57m−4.55m=0.02m
- Initial temperature, T1=27∘C (room temperature)
- Final temperature, T2=100∘C
- Change in temperature, ΔT=T2−T1=100∘C−27∘C=73∘C
Since the change in temperature in Celsius is the same as in Kelvin, we can directly use:
ΔT=73K
Now, substituting the values into the formula for ΔL:
0.02=4.55⋅α⋅73
Rearranging the equation to solve for α:
α=0.024.55⋅73
4.55⋅73=332.15
α=0.02332.15≈6.021×10−5K−1
The coefficient of linear expansion α of the given wire is approximately:
α≈6.021×10−5K−1
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Specific Heat Capacity
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Calorimetry
4 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Measurement Of Temperature
2 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
When a metallic bar is heated from 0∘C to 100∘C its length increases by 0.05%. What is the coefficient of linear expansion of the metal?
View SolutionThe length of a rod increases from 50 cm to 50.12 cm, when its temperature is increased from 12∘C to 212∘C . Calculate its coefficient of liner expansion.
View Solution
Knowledge Check
Length of wire at room temperature is 4.55 m , when the temperature increases up to 100∘C then its length becomes 4.57 m . The coefficient of linear expansion (α) of the given wire is
A5.021×10−5K−1B6.021×10−5K−1C7.021×10−5K−1D8.021×10−5K−1The volume of a metal sphere increases by 0.15% when its temperature is raised by 24∘C. The coefficient of linear expansion of metal is
A2.5×10−5/∘CB2.0×10−5/∘CC1.5×10−5/∘CD12×10−5/∘CA steel wire 2 mm in diameter is just stretched between two fixed points at a temperature of 20∘C. If the temperature falls to 10∘C, then the tension in the wire is (The coefficient of linear expansion of steel = 11×10−6/∘C and Y for steel 2.1×1011N/m2)
A7.25 NB725 NC72.5 ND7.25×103N
By how much amount should the temperature of a steel rod be increased so that its length increases by 0.5%? The coefficient of linear expansion of steel is 1.2×10−5C−1
View Solution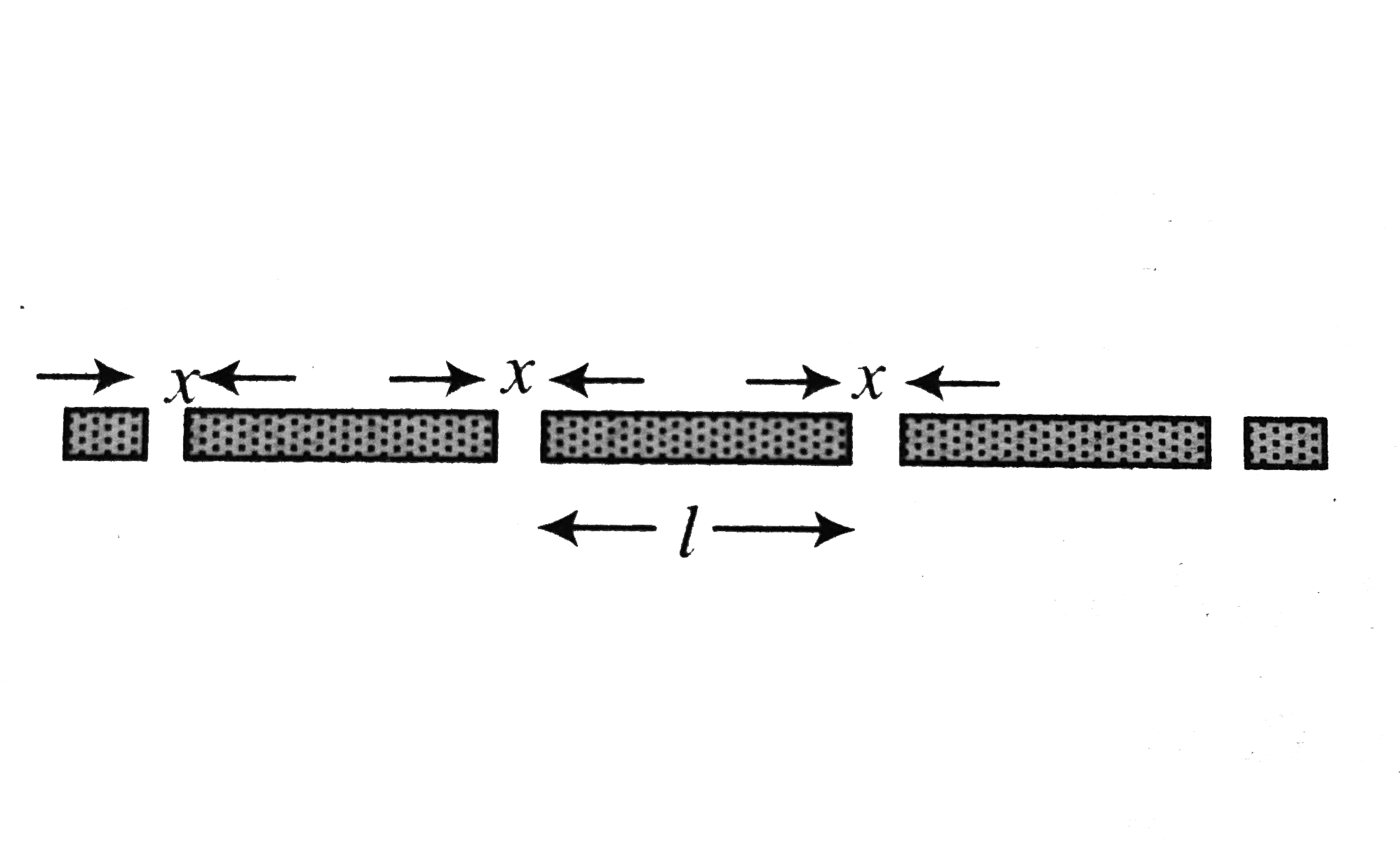
The gap between any two rails each of length l laid on a railway trach equals x at 27∘C When the temperature rises to 40∘C the gap closes up. The coefficient of linear expansion of the material of the rail is α. The length of a rail at 27∘C will be
View SolutionA wire of length 100cm increases in length by 10−2m when it is heated through 100∘C. The coefficient of linear expansion of the material of the wire exprassed in /K units is
View SolutionA steel wire 2 mm is diameter is just stretched between two fixed points at a temperature of 20∘C. If the temperature falls to 10∘C, then the tension in the wire is (Coefficient of linear expansion of steel (α) is 11×10−6/∘CandYs=2.1×1011N/m2)
View SolutionThe volume of a metal sphere increases by 0.24% when its temperature is raised by 40∘C . The coefficient of linear expansion of the metal is .......... .∘C
View Solution
